PeiLingX
物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》的第8课。
了解本系列其他文章,请收藏目录:
0) 开篇语
在第1课到第6课中,我们通过对态矢量和特征值理论的理解,一点点体会到了量子力学的数学原理。
但那毕竟还只是在更接近数学的纯精神世界中寻求快感,而不是在真实的物理世界中真刀真枪实战。
而在第7课中,我们为顺利进入具体物理世界进行了一次铺垫,直观上感受了向量与函数的联系,为我们拜谒量子力学的主角做好了最后的准备。
接下来,我们就可以召唤量子力学中的两大主角:波函数 (Wave Function)和薛定谔方程 (Schrödinger Equation )隆重登场了。
1) 波函数与坐标表象
还记得我们在第1课开头就提到过的那条“量子力学描述物理世界的方式”吗:
相比于经典力学中用具体的力学量描述物理对象的状态,量子力学中,描述物理状态只需要一个态矢量,它包含了一个物理对象一切力学量的概率信息(而不仅仅是位置 )。
而态矢量的具体表现形式,就是描述“波粒二象性”中那个“波”的波函数。
根据我们对“波”的理解,它描述的是某种振动在空间中的传播。
由于振动牵涉到时间,而传播依赖于空间,所以一个波函数,通常可以描述为空间和时间的函数,我们将它记为:
ψ(x,y,z,t)
那么,抽象的态矢量是怎么和一个具体的函数联系起来的呢?
笼统地说,是一种“投影”关系将它们联系了起来。
而这种投影关系,有一个听起来很高端、高端到可以用来忽悠无知小学妹的名字,叫做“坐标表象”。
接下来我们就先来具体解释一下,什么是“表象”。
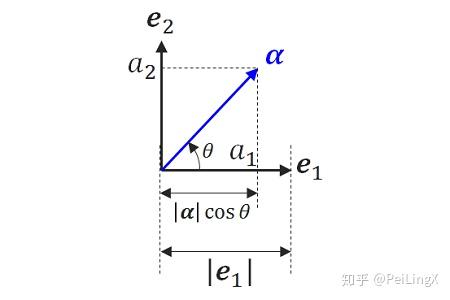
在线性代数中我们知道,对于同一个向量,选择不同的基底,会得到不同的分量形式。
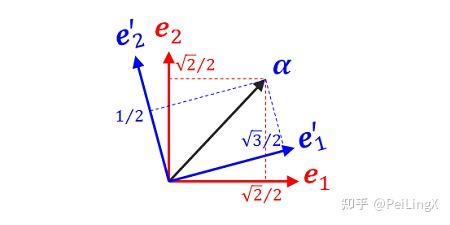
比如上面图中的向量 α ,在基底 e1,e2 下,分量形式为:
(a1,a2)=(√22,√22)T(式8.1)
在基底 e′1,e′2 下,分量形式为:
(a′1,a′2)=(√32,12)T(式8.2)
而我们在第7课中,已经理解了如何将一个函数在各点的函数值类比为向量在各个基底上的分量。
那么,现在将向量类比为态矢量,将向量的分量形式类比为函数形式,我们就能理解什么是表象了:
对于同一个抽象的态矢量 |ψ⟩ 而言,一个“表象”就对应一组基底。我们说的“某某表象”,就是态矢量在某个力学量的本征态基底下的“投影”组成的函数形式。
比如当我们关注坐标时,选取坐标的本征态作为基底,它就表现为我们熟悉的波函数形式 ψ(x,y,z,t) ,这就叫作态矢量的“坐标表象”(Coordinate Representation);
(顺便说一句,在量子力学里,坐标的本征态在数学上并没有一个良好的定义,有兴趣可以看看这个链接中的讨论。但这里我们先不用理会数学上的严谨性,因为它不会影响我们的理解 )
而当我们关注动量时,选取动量的本征态作为基底,那么我们会得到另外一个波函数形式 ϕ(px,py,pz,t),这就叫做态矢量的“动量表象”(Momentum Representation)。
这里顺便多说一句:
我们知道,在不同基底之间,同一个向量的分量形式存在某种变换关系,而态矢量的两种表象的波函数之间,也有一定的变换关系,叫做“表象变换”。
比如坐标表象和动量表象之间,就满足某个非常有名的变换关系,它是我们将来推导不确定性关系的核心。
各位不妨猜一猜这是什么变换,我们在以后讲表象变换时再来揭晓。
现在我们回到坐标表象下的波函数 ψ(x,y,z,t)
我们要来看看,如何由它得到一个物理对象的力学量的概率信息,以及如何引出本文的第二个主角:薛定谔方程。
2) 力学量的概率信息
为了便于理解,我们先忽略波函数随时间变化的情况,并且先只考虑坐标表象下的一维情形,此时波函数仅仅是 x 坐标的函数: ψ(x)
理论上,给定了具体的波函数,我们就能找出任意经典力学量的概率信息。
不管是位置(即坐标 )、动量还是能量……只要有足够的信息,我们都能找出它们的概率分布来。
比如,有这么一个结论,熟读量子力学科普、并且可能接触过一些量子力学教材的我们,大概都听说过:
按照哥本哈根诠释,波函数的模方 |ψ(x)|2代表一个物理对象在坐标为 x 的位置出现的概率密度。
这里其实说的就是如何从波函数中得到一个物理对象的位置的概率分布信息。
只不过,在没有理解态矢量之前,我们只能将它看成一个不明所以的物理事实。
但现在我们有了态矢量的思维方式,就可以更进一步理解它的数学本质了。
首先,我们知道,位置作为一个力学量,会对应一个算符、以及一系列本征值和本征态。
我们将位置算符记作 ˆx ,它的本征值,就是所有可能被我们测量到的坐标值 x ,而相应的本征态记作 |x⟩
(虽然前面说了,坐标的本征态并没有一个良好的定义,但我们可以继续假装这个问题不存在 )
按照我们第2课中知道的性质,对于处于任意量子态(不一定是本征态 ) |ψ⟩ 的物理对象而言,当我们去测量它的位置坐标时,测到它位于某个位置 xa 处的概率为:
f(xa)=|⟨xa|ψ⟩|2(式8.3)
(注意:由于空间坐标是连续的,所以这里的“概率”通常指的是概率密度 )
但这毕竟只是一个不可计算的抽象式,怎么把它转化成我们正在讨论的波函数形式呢?
首先,我们已经知道了,坐标表象下, |ψ⟩ 对应的波函数表示为 ψ(x)
而接下来,我们需要找到本征态 ⟨xa| 对应的波函数。
在这里,有一点非常特殊的是:我们是在坐标表象下求坐标自身的本征态的函数形式。
这类比到线性代数中,其实就有点像向量空间中给定一组正交归一的基底后,求这些基底自身的分量形式。
而我们知道,如果以自身为基底,那么向量空间中的基向量就是这样的简单形式:
{e1=(1,0,⋯,0)Te2=(0,1,⋯,0)T⋮en=(0,0,⋯,1)T(式8.4)
也就是说,某个基向量 ek 的分量中,只有第 k 个分量等于1,在其他分量上都为0.
现在我们将它类比到函数空间上。
我们似乎有理由猜测,对于坐标表象下的坐标本征态、也就是基底 ⟨xa|本身而言,它应该是这样一个函数:
当 x=xa 时函数值为1,而当 x≠xa 时函数值为0.
但我们很快会发现这样定义有问题,因为我们要求一个态矢量必须具有归一化条件,即函数在坐标空间上的积分为1,但上面定义的函数只在一个点上不为0,其余点上处处为0,那么它的积分显然是0.
但联系到前面提到的向量空间中的类比,无论如何,“当 x≠xa 时函数值为0”这个条件是应该保留的,那么我们就需要找一个函数,它在 x≠xa 时函数值处处为0,但在坐标空间中的积分为1.
实际上,这样的函数并不存在于我们熟悉的初等函数中。它是一种特殊函数,由狄拉克发明,名叫δ函数。
它的定义就是我们刚才提到的两个条件:
- δ(x−xa)=0(if x≠xa)(式8.5a)
- ∫Rδ(x−xa)dx=1(式8.5b)
对于本征值 xa 对应的本征态 |xa⟩和⟨xa| ,它们在坐标表象下的波函数都是同一个δ函数: δ(x−xa)
读到这里,细心的同学可能会发现,这个定义意味着δ函数在 x=xa处为无穷大,即:
δ(x−xa)={∞x=xa0x≠xa(式8.6)
这里突然出现的无穷大,似乎让我们的计算变得困难起来(因为∞无法参与计算 ),但幸运的是,我们在实际运算中只需要用到它的积分性质,也就是δ函数定义的第二条:
∫Rδ(x−xa)dx=1(式8.5b)
而在此基础上,我们还能得到δ函数的另外一个更加令人喜爱的性质,那就是δ函数和任意一个平方可积函数相乘后积分的结果:
∫+∞−∞δ(x−xa)ψ(x)dx=ψ(xa)(式8.7)
而我们在第7课中已经知道,这正好就是两个函数的内积运算:
∫+∞−∞δ(x−xa)ψ(x)dx=⟨xa|ψ⟩=ψ(xa)(式8.8)
这样, ψ(xa) 也就可以看成态矢量 |ψ⟩在位置本征态 ⟨xa|上的“投影”、也就是线性组合的系数。
将所有的 xa上的“投影”、即 ψ(xa) 组合起来,就组成了波函数 ψ(x)
这就是为什么我们说波函数是态矢量的坐标表象了。
而根据波函数的“投影”性质,我们不难将它和物理对象的状态坍缩到坐标本征态 ⟨xa| 、也就是物理对象出现在某个位置 xa 的概率联系起来:
f(xa)=|⟨xa|ψ⟩|2=|∫+∞−∞δ(x−xa)ψ(x)dx|2=|ψ(xa)|2(式8.9)
这就得到了哥本哈根解释里描述的那个样子。
(对于三维情形,物理对象在空间中某点 (x,y,z) 出现的概率密度就是 |ψ(x,y,z)|2 )
到这里,我们就对波函数以及它的概率诠释有了更加“几何化”的理解。
现在,说完了坐标,让我们将注意力转移到一个更重要的力学量上:能量。
3) 能量与定态薛定谔方程
能量算得上是量子力学中最重要的力学量。
(量子态当然更重要,但它并不是一个力学量 )
从理论和美学的角度来说,能量决定了量子态如何随时间演化(我们待会儿就会看到 ),也是我们将来理解量子力学中的对称性和守恒律的基础;
而从现实的角度来说,能量也是量子力学走向实用化的最关键信息:
比如对于某种元素或材料而言,讨论它在原子级别的能量概率分布,有助于我们推算元素和材料的宏观性质,这被称为第一性原理计算(First Principle Calculation)。它是将化学和材料科学从不断试错的“炼金术”升级为有章可循的科学计算的必经之路。
(关于这一点,我们将在另一个系列:身边的微分方程中介绍 )
而在前面的讨论中,我们可以看到,要计算物理对象出现在某个位置的概率密度,需要先找到这个位置对应的本征态的波函数形式。
同理,寻找能量概率分布的关键步骤,就是找到能量的本征值和相应本征态的波函数形式。
为了实现这一点,我们需要先从能量的算符说起。
在第6课中我们曾经介绍过,能量的算符叫作哈密顿算符,记作 ˆH 。
(其实要写成 ˆE 也无妨,但因为能量算符的性质与分析力学紧密相连,而分析力学中能量又被称作哈密顿量,所以能量算符也就称作哈密顿算符了,没学过分析力学的同学可以先忽略这点,以后我们需要的时候再来具体介绍 )
相应的能量本征值系列我们记为 Ea ,本征态系列记为 |a⟩ 。
根据第6课中提到的能量算符的本征值关系,我们知道:
ˆH|a⟩=Ea|a⟩(式6.10)
这个式子将是我们寻找能量本征态的关键,因为只要我们确定了哈密顿算符在某个表象(比如坐标表象 )中的具体形式,理论上,我们就能将上面的式子变成一个方程,然后求解出相应的能量本征值和本征态。
这里顺便说一句,和态矢量类似,一个算符在不同的表象下,也有不同的形式,就像线性代数中同一个线性变换,在不同基底下表现成不同的矩阵形式一样(这些矩阵互为相似矩阵 )。
所以,当我们要进行具体计算的时候,需要找出一个算符在某个表象下的具体形式,就像计算矩阵特征值的时候需要一个具体的矩阵一样。
那么,如何找到哈密顿算符的具体形式呢?这需要我们回到经典力学中寻找一些启发……
我们知道,在经典力学中,一个物体的总能量等于动能加势能:
E=T+V(式8.10)
而动能为:
T=p22m(式8.11)
(不考虑转动的情形下 )
于是总能量就是:
E=p22m+V(式8.12)
到了量子力学中,这样的能量关系仍然被保留了下来。
只不过,经典力学中的能量、动量、势能,到了量子力学中都变成了算符,于是上面的关系式变成了:
ˆH=ˆp22m+ˆV(式8.13)
这样,哈密顿算符作用在态矢量上的形式就变成了:
ˆH|ψ⟩=(ˆp22m+ˆV)|ψ⟩(式8.14)
你也许要问了:这不就是把经典力学的量都换成算符了吗?我们还是没有算符的具体形式啊?
别着急,如果我们知道了动量算符和势能算符在坐标表象下的具体形式,再结合 |ψ⟩ 的波函数形式,问题就有谱了。
为了让表述简单化,我们仍然来考虑一维的、且系统不随时间变化的情况:
首先,在具体的物理场景中,势能的空间分布是一个已知量: V(x) ,可以认为这就是坐标表象下势能算符 ˆV 的具体形式 (三维情形下为 V(x,y,z) )
而动量算符的形式有点反直觉,这里我们先不加解释(解释放到下节课 )、直接给出它的形式:
在一维情形的坐标表象下,动量算符是关于坐标的微分算子:
ˆp=−iℏ∂∂x(式8.15)
不难想象,在三维情形的坐标表象下,动量算符是一个梯度算子:
ˆp=−iℏ∇=−iℏ(∂∂x,∂∂y,∂∂z)(式8.16)
再考虑到 |ψ⟩=ψ(x) ,将三者代入算符版本的能量关系式,我们就得到了:
ˆH|ψ⟩=(−ℏ22m∂2∂x2+V)ψ(x)(式8.17)
相应的三维版本就是:
ˆH|ψ⟩=(−ℏ22m∇2+V(x,y,z))ψ(x,y,z)(式8.18)
如果将能量本征态的波函数形式记为 ψa(x) ,那么根据算符与本征态的关系: ˆH|a⟩=Ea|a⟩ ,我们就能得到:
(−ℏ22m∂2∂x2+V)ψa(x)=Eaψa(x)(式8.19)
看出来了吗?这是一个微分方程,准确说,是一个典型的定态薛定谔方程。
(当然,它还不是我们更熟悉的那个薛定谔方程本尊,而只能算是薛定谔方程的空间部分 )
解出这个方程,我们就能得到物理对象的能量在相应物理情形下的本征值和本征态,从而利用态矢量与本征态的内积关系,求出物理对象处于某种状态时的能量概率分布。
但这牵涉到方程的求解,本课暂不讨论。
在这里,我们更愿意去庆贺一件事情,就是我们又一次看到了代数方程和微分方程、特征向量和本征态之间的异曲同工之妙。
不过,到此为止,我们这节课的任务还没结束,因为现在给出的定态薛定谔方程,还没有包含量子态的全部信息。
怎么理解这句话呢?
在经典力学中,我们知道,给定了一个物体当前的状态(位置、动量等 )以及周围的物理环境(势能分布或者力场分布 ),那么我们就能根据牛顿定律列出动力学方程,求解物体的状态未来随时间的演化。
量子力学中,我们也需要一个能够求解量子态随时间演化的方程。
而前面的定态薛定谔方程中没有包含时间,也就无法告诉我们量子态怎么随时间演化。
接下来,我们就要来补充量子态随时间演化的规律。
4) 量子态的演化
前面我们提到,量子态的演化和能量有关,说得再具体一点,其实是和哈密顿算符有关。
现在我们先不加解释地给出它的演化规律:
∂∂t|ψ⟩=ˆHiℏ|ψ⟩(式8.20)
也就是说,量子态的演化可以看作哈密顿量作用在态矢量上的结果。
同学们一定很好奇:这个关系是怎么来的?
这一点,我们会分两次来解释:
下节课中,我们会从一个著名的物理事实出发来得到,而未来我们还会从更抽象但也更具有对称性的角度来说明。
现在我们回到演化方程本身,看看它在坐标表象下的具体形式。
首先,我们将 iℏ 移到左边,然后将前面给出的坐标表象下哈密顿算符的具体形式、即式8.17代入演化方程(式8.19),我们就能得到一个新的微分方程:
iℏ∂∂tψ(x,t)=(−ℏ22m∂2∂x2+V)ψ(x,t)(式8.20)
相应的三维版本就是:
iℏ∂∂tψ(x,t)=(−ℏ22m∇2+V(x,y,z))ψ(x,y,z,t)(式8.21)
怎么样,熟悉这个式子吗?
没错,这就是我们在科普书或量子力学教材中屡次相见、却一直不明所以的薛定谔方程的本尊。
神奇吗?我们并没有特意追寻前人步伐、去了解过任何量子力学发展史,而仅仅凭借几个简单的线性代数假设、和很少一点经典力学的知识,也能“不经意地”走到这个里程碑面前。
4) 总结与预告
到此为止,我们终于来到了量子力学的正殿,拜见了量子力学的两个重要主角。
但更重要的是我们见到它们的方式:通过从第1课开始一路的领悟,用富有“几何意义”的线性代数关系、自然而然地引出了他们。
此时相见,他们不再仅仅是一堆纷乱且反直觉的物理现象,而是蕴涵着深刻而优美的代数本质:
- 波函数 = 态矢量在坐标表象下的具体函数形式,类似于向量在某一组基底下的具体分量形式;
- 定态薛定谔方程 = 能量的本征值关系在坐标表象下展现出的一个具体微分方程形式;
- 薛定谔方程 = 量子态的时间演化规律在坐标表象下展现出的一个具体微分方程形式。
这些数学本质将有助于我们继续用这种“悠然见南山”的方式去“发现”和理解更多结论,这一点,我们将会在后面的课程中体会到。
而眼下,我们需要回头来交待前文遗留下来的两个问题:
- 为什么坐标表象下的动量算符的形式为 ˆp=−iℏ∂∂x
- 为什么态矢量的时间演化满足关系式 ∂∂t|ψ⟩=ˆHiℏ|ψ⟩
如果想偷懒的话,我们其实可以将这两个结论本身直接看成一个物理事实,只是这样的表述更不“自然”而已。
而导出这两个结论的更“自然”的方式有两种:一种是从一个我们熟知的物理事实出发来得到,另一种是从一个更抽象也更有美感的数学关系出发来得到。
第二种对于现在的我们来说理解起来还有点难度,所以下节课我们先用第一种方式出发来得到它:
编辑于 2021-11-30 13:24