PeiLingX
物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》的第12课。
了解本系列及本专栏其他文章，请收藏目录：
0) 开篇语
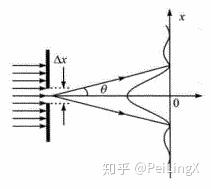
上节课中，我们用单缝衍射实验的结果定性地展现了不确定性原理的最典型的例子：
位置和动量的不确定性关系。
而我们知道，位置和动量之间的不确定性，可以用两者的标准差$ \small \Delta x,\Delta p $定量表示成这样一个著名的不等式：
$\small \Delta x\Delta p\geq\frac{\hbar}{2} \quad\scriptsize{(式11.1)}$
(为了方便理解，我们只讨论一维模型，因此动量符号$ \small p $下面不再标注下标)
这描述了位置和动量不确定度的此消彼长：一个分布越集中，另一个就越分散。
而在文章的最后，我们提到，这种“此消彼长”的关系背后，也暗藏着一个线性代数原理：基底变换，而量子力学中我们将它称作表象变换。
理解了这种变换关系，我们就能找出一个物体的位置分布和动量分布之间的关系，最终理解不确定性原理的数学本质、并且导出那个著名的不确定性关系式。
为了更直观理解这种变换，我们还是先从二维平面的例子说起。
1) 表象：二维平面的直观例子
我们先假设，二维平面上分别有两组线性无关的基底：$ \small {\boldsymbol\alpha_1,\boldsymbol\alpha_2} $以及$ \small {\boldsymbol\beta_1,\boldsymbol\beta_2}$
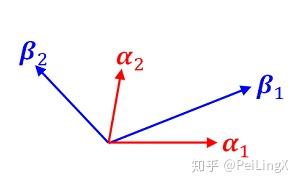
现在给定一个向量$ \small \boldsymbol u $，那么它分别在以$ \small {\boldsymbol\alpha_1,\boldsymbol\alpha_2} $为基底和以$ \small {\boldsymbol\beta_1,\boldsymbol\beta_2} $为基底时，坐标分量(也就是在两组基底上的投影)是不同的：
我们不妨把这两种分量形式换成量子力学语言，分别叫做“$ \small \alpha $表象”和“$ \small \beta $表象”。
而现在，我们要关心的是，两种“表象”之间的变换关系。
在线性代数中我们知道，这可以从$ \small {\boldsymbol\alpha_1,\boldsymbol\alpha_2} $与$ \small {\boldsymbol\beta_1,\boldsymbol\beta_2} $本身之间的变换关系来得到。
我们这就来复习一遍。
2) 表象变换：二维平面的直观例子
为了方便理解，我们用不带上标的粗体字母、比如$ \small \boldsymbol u $、来代表向量本身，这与基底选取无关。而当我们在某个具体的表象下写出它的分量形式时，则加上与基底相应的上标，比如在“$ \small \alpha $表象”下，$ \small \boldsymbol u $的分量形式为：
$\small \boldsymbol u^{(\alpha)}=(u_1^{(\alpha)},u_2^{(\alpha)})^T \quad\scriptsize{(式12.1)}$
如果我们将$ \small \boldsymbol u^{(\alpha)} $当作已知条件，那么只要我们再给出基底$ \small {\boldsymbol\alpha_1,\boldsymbol\alpha_2} $在基底$ \small {\boldsymbol\beta_1,\boldsymbol\beta_2} $下的分量形式，我们就能求出$ \small \boldsymbol u $的“$ \small \beta $表象”、即$ \small \boldsymbol u^{(\beta)} $的分量形式了。这样我们就得到了$ \small \alpha $和$ \small \beta $两种“表象”(两个基底)的变换关系。
根据前面的约定，我们将基底$ \small {\boldsymbol\alpha_1,\boldsymbol\alpha_2} $的“$ \small \beta $表象”分别记为：
$\small \begin{cases} \boldsymbol\alpha_1^{(\beta)}&=\left( \matrix{a^{(\beta)}_{11} & a^{(\beta)}_{21}} \right)^T\\ \boldsymbol \alpha^{(\beta)}_2&=\left( \matrix{a^{(\beta)}_{12} & a^{(\beta)}_{22}} \right)^T \end{cases} \quad\scriptsize{(式12.2)}$
这里其实说明了两组基底之间的线性叠加关系：
$\small \begin{cases} \boldsymbol\alpha_1&=a^{(\beta)}_{11}\boldsymbol\beta_1+a^{(\beta)}_{21}\boldsymbol\beta_2\\ \boldsymbol\alpha_2&=a^{(\beta)}_{12}\boldsymbol\beta_1+a^{(\beta)}_{22}\boldsymbol\beta_2 \end{cases} \quad\scriptsize{(式12.3)}$
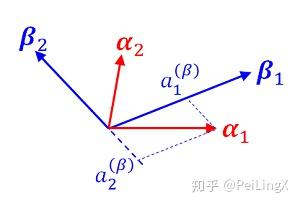
α1的“β表象”
有了这个关系，我们就能得到：
$\small \begin{align} \boldsymbol u&=u_1\boldsymbol\alpha_1+u_2\boldsymbol\alpha_2\\ &=a^{(\beta)}_{11}u_1\boldsymbol\beta_1+a^{(\beta)}_{21}u_1\boldsymbol\beta_2+a^{(\beta)}_{12}u_2\boldsymbol\beta_1+a^{(\beta)}_{22}u_2\boldsymbol\beta_2\\ &=\left(a^{(\beta)}_{11}u_1\boldsymbol+a^{(\beta)}_{12}u_2\right)\boldsymbol\beta_1+\left(a^{(\beta)}_{21}u_1\boldsymbol+a^{(\beta)}_{22}u_2\right)\boldsymbol\beta_2 \end{align} \quad\scriptsize{(式12.4)}$
写成矩阵形式，就是我们熟悉的基底变换关系：
$\small \begin{bmatrix} u^{(\beta)}_{1}\\u^{(\beta)}_{2} \end{bmatrix} =\begin{bmatrix} a^{(\beta)}_{11}&a^{(\beta)}_{12}\\ a^{(\beta)}_{21}&a^{(\beta)}_{22} \end{bmatrix}\begin{bmatrix} u^{(\alpha)}_{1}\\u^{(\alpha)}_{2} \end{bmatrix} \quad\scriptsize{(式12.5)}$
不过，为了方便后面讨论，我们还是将上式写成求和形式：
$\small u^{(\alpha)}_i\ \rightarrow \ u^{(\beta)}_i=\sum_j{a^{(\beta)}_{ij}u^{(\alpha)}_j} \quad\scriptsize{(式12.6)}$
也就是说，只要给出了两个信息：
- 基底$ \small {\boldsymbol\alpha_j} $的“$ \small \beta $表象”、即$ \small a^{(\beta)}_{ij}$
- 向量$ \small \boldsymbol u $的“$ \small \alpha $表象”、即$ \small u^{(\alpha)}_j$
我们就能找到任意向量在两个基底之间的变换$ \small u^{(\alpha)}_i\ \rightarrow \ u^{(\beta)}_i $，这也是我们在线性代数中已经熟知的内容。
现在，我们将这种关系推广到量子力学中去。
3) 表象变换：动量与坐标
在第8课中，我们提到过，一个态矢量或算符在力学量$ \small F $中的表象，就是它在$ \small F $的本征态构成的基底下的具体形式。
当我们用位置坐标的本征态作为基底，来表示一个态矢量的时候，得到的就是坐标表象，而用动量的本征态作为基底，就得到动量表象。
为了方便结合物理事实讨论，我们现在将一个态矢量的动量表象作为已知条件，然后利用线性代数基底变换的思路，来找出它的坐标表象，这样我们就能得到两个表象之间的变换关系。
我们先来考虑离散的情形，即动量的本征值是一个离散序列，记为$ \small {p_n} $，又将相应的本征态序列记为$ \small {\left|p_n\right>} $。那么任意态矢量$ \small \left|\psi\right> $都可以表示成相应的动量本征态的叠加，记为：
$\small \left|\psi\right>=\sum_n{\phi_n\left|p_n\right>} \quad\scriptsize{(式12.7)}$
这样，系数序列$ \small {\phi_n} $就构成$ \small \left|\psi\right> $的动量表象。
现在我们来找出$ \small \left|\psi\right> $的坐标表象。
仿照线性代数中基底变换的推导思路，我们不难得知：
在已知$ \small \left|\psi\right> $的动量表象的前提下，只要能找到动量本征态$ \small \left|p_n\right> $的坐标表象，我们就能找出$ \small \left|\psi\right> $的坐标表象。
首先，我们在第8课中知道，一个态矢量的坐标表象，就是通常意义上的波函数，这里我们将动量本征态的波函数记为$ \small \psi_{p_n}(x)$
而根据动量本征态的定义，我们又知道，当一个物体处于某个动量本征态$ \small \left|p_n\right> $时，它就具有确定的动量值。
根据德布罗意关系，这就意味着，它的波函数是一个具有确定波数$ \small k $的正弦波，我们用复指数形式，记为：
$\small \psi_{p_n}(x)=\text e^{\text i \frac{p_n}{\hbar}x} \quad\scriptsize{(式12.8)}$
这就正是动量本征态$ \small \left|p_n\right> $的坐标表象了。
现在，我们仿照上一节中给出的二维平面上的基底变换关系：
$\small u^{(\alpha)}_i\ \rightarrow \ u^{(\beta)}_i=\sum_j{a^{(\beta)}_{ij}u^{(\alpha)}_j} \quad\scriptsize{(式12.9)}$
将其中$ \small \boldsymbol u $的“$ \small \alpha $表象”$ \small u^{(\alpha)}_i $替换为$ \small \left|\psi\right> $的动量表象$ \small {\phi_n} $、将基底$ \small {\boldsymbol \alpha_1,\boldsymbol \alpha_2} $的“$ \small \beta $表象”$ \small a^{(\beta)}_{ij} $替换为动量本征态的坐标表象$ \small \text e^{\text i \frac{p_n}{\hbar}x} $，就能写出$ \small \left|\psi\right> $的坐标表象的表达式：
$\small \psi(x)=A\sum_n{\phi_n\text e^{\text i \frac{p_n}{\hbar}x}} \quad\scriptsize{(式12.10)}$
可以看出，这是一个由动量本征态的波函数构成的傅里叶级数。
接下来，我们将这个结论推广到连续情形。
不考虑严谨性的话，这个推广其实就很简单了：
连续情形下，动量本征值具有连续取值，于是态矢量$ \small \left|\psi\right> $的动量表象自然就是以动量为自变量的函数$ \small \phi(p)$ (相当于离散情形下的序列 $\small {\phi_n}$ )
而此时的动量表象$-$坐标表象的变换关系式，也就是将求和换成积分，同时在动量本征态的波函数(坐标表象)前面加一个归一化系数$ \scriptsize A=\frac{1}{\sqrt{2\pi \hbar}}$ (以保证全空间的概率积分为1)，于是我们得到：
$\small \psi(x)=\frac{1}{\sqrt{2\pi \hbar}}\int{\phi(p)\text e^{\frac{\text i}{\hbar}px}\text dp} \quad\scriptsize{(式12.11)}$
这个积分是不是很熟悉？
对，你没看错，动量表象与坐标表象之间的变换关系，就是那个总会在我们意想不到的地方出现、带给我们惊喜的跨界大佬：傅里叶变换。
下一课中，我们就要用这个变换关系来最终给出不确定性原理的那个重要关系式：
$\small \Delta x\Delta p_x\geq\frac{\hbar}{2} \quad\scriptsize{(式11.1)}$
不过，结束全文之前，我们还要来顺便完成另一件支线任务。
4) 波粒二象性
还记得我们第1课开篇中提到的几个疑惑中有一个关于波粒二象性的吗：
我们知道微观粒子具有波粒二象性，物理课本告诉我们，微观粒子既是粒子又是波，但我们其实只是记住了这句话，这种奇怪的二重性质有没有更好的理解方式呢？
现在我们可以从态矢量和表象的角度来理解它了：
当我们将一个粒子的态矢量$ \small \left|\psi\right> $放到动量表象下时，它就变成了动量本征态的线性叠加：
$\small \left|\psi\right>=\sum_a \phi(p_a)\left|p_a\right> \quad\scriptsize{(式12.12)}$
而根据德布罗意关系，一个动量本征值对应着一个单色波的波数$ \small k_a=\frac{p_a}{\hbar} $，于是这个时候态矢量就可以看成一系列单色波的叠加，这就可以理解为它的波动性质。
而如果我们将它放到坐标表象下，它就变成了坐标本征态的线性叠加：
$\small \left|\psi\right>=\sum_a \psi(x_a)\left|x_a\right> \quad\scriptsize{(式12.13)}$
特别是，当我们去测量它的位置时，它就会以概率$ \small \left|\psi(x_a)\right|^2 $随机坍缩到一个坐标本征态$ \small \left|x_a\right> $上，这时候我们就在$ \small x=x_a $这个位置上找到了它，它也就体现出了粒子的属性。
5) 结语与预告
本课中，我们用二维平面上的基底变换作为直观类比，结合德布罗意关系，推导了态矢量的动量表象和坐标表象之间的变换式，最后惊奇地发现，它竟然就是傅里叶变换。
这不仅暗示了傅里叶变换与量子力学的微妙联系，也暗示了傅里叶变换背后的线性代数本质。实际上，傅里叶变换本身，就是“无穷维”空间上一种最重要的基底变换之一。
而鉴于傅里叶变换的神光已经照耀了理工科的半壁江山，在进入下一课之前，我们不妨先开一个番外篇，来梳理一下傅里叶变换与线性代数基底变换的类比关系：
$($链接待更新$)$
想跳过这段支线剧情的同学，请直接进入下一课。
编辑于 2021-11-30 14:46
