PeiLingX
物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》第20课。
本系列及本专栏其他文章,建议收藏目录:
0) 开篇语
如果我们随手翻开一本量子力学书,翻到关于求解球对称问题或氢原子问题那一节,我们会看到教材作者非常耐心地教我们,如何通过反复使用一种名叫“分离变量法”的方法,一层层得到最终的解。
然而,这样跟着教材计算一遍之后,我们可能会有这样的感觉:这个求解过程就是解线性偏微分方程的一种标准程序,代数或物理上并没有什么意义。
而作为一名普通的物理爱好者,我们当中很多人甚至从来都没系统学过偏微分方程,所以求解过程对我们来说似乎也就更没有观赏的必要,不如直接把进度条拉到最后,去看看最终的解长什么样子。
但这其实是一种错觉,这节课中我们会看到,这个求解过程中蕴含着非常有意思的代数内涵(其实也是分离变量法这套标准程序的代数内涵)。并且,只有理解了求解过程,我们才能更深刻地理解方程解的物理意义。
前面,我们用了两节课时间来为此做了足够的准备,现在一切水到渠成,我们可以来体验这个过程了。
1) 求解思路
我们先来回望一眼球坐标形式的薛定谔方程:
$\small -\frac{\hbar^2}{2m_e}\left[\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial \psi}{\partial r}\right)+\frac{1}{r^2\sin\theta}\frac{\partial }{\partial \theta}\left(\sin\theta\frac{\partial \psi}{\partial \theta}\right)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2 \psi}{\partial \varphi^2}\right]+V(r)\psi=E\psi \quad{\scriptsize (式18.7)}$
我们知道,求解这个方程的目的,就是找到能量的本征值和本征态。
如果没有前面两节课的铺垫,我们会觉得这个问题非常棘手:因为这个方程当中,三个变量$ \small r,\theta,\varphi $相互交织,一团乱麻。
但好在我们在第18课中讨论过方程左边各项的物理意义,在这个基础上,我们其实是可以找到一条清晰的求解思路的。
简单来说,这个思路就是我们对付一支联合部队时经常用的办法:
分化瓦解,各个击破。
对应到我们的求解过程,就是将这个偏微分方程分化为几个相互独立的常微分方程(毕竟这是更容易求解的),然后逐个搞定。
具体操作上,我们可以先挑一个看起来好下手的搞定,然后环环解扣、解决剩下的麻烦。
下面我们就先来寻找这个软柿子。
根据第18课中的讨论,我们可以先将这支“哈密顿联军”分成径向和角向两个军团:
$\small \begin{align} E\left|\psi\right>&={\scriptsize -\frac{\hbar^2}{2m_e}\left[\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial }{\partial r}\right)+\frac{1}{r^2\sin\theta}\frac{\partial }{\partial \theta}\left(\sin\theta\frac{\partial }{\partial \theta}\right)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2 }{\partial \varphi^2}\right]\psi+V(r)\psi}\\ &={\scriptsize \left[-\frac{\hbar^2}{2m_e}\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial }{\partial r}\right)+V(r)\right]\psi-\frac{\hbar^2}{m_er^2}\left[\frac{1}{\sin^2\theta}\frac{\partial }{\partial \theta}\left(\sin\theta\frac{\partial }{\partial \theta}\right)+\frac{1}{\sin^2\theta}\frac{\partial^2 }{\partial \varphi^2}\right]\psi}\\ &=\left(\frac{1}{2m_e}\hat p_r^2+\hat V\right)\left|\psi\right>+\frac{1}{2m_er^2}\hat L^2\left|\psi\right> \end{align} \quad{\scriptsize (式20.1)}$
而第19课中,我们知道,角动量平方算符$ \small \hat L^2 $与哈密顿算符是相互对易的,也就是说,哈密顿算符的本征态也是$ \small \hat L^2 $的本征态。
这就提示我们,假如某个态$ \small \left|\psi\right> $是薛定谔方程的解、也就是它满足哈密顿算符的本征方程,那么它同样也应该满足角动量平方算符的本征方程,我们不妨将这个方程写为:
$\small \hat L^2\left|\psi\right>=\lambda\left|\psi\right> \quad{\scriptsize (式20.2)}$
这个关系先放在这里,我们待会儿就会用到。
接下来,我们继续对“角向军团”进行分化瓦解。
同样是根据第18课中的讨论,我们可以将这支“角向军团”分成垂直于$ \small z $轴和平行于$ \small z $轴的两部分:
$\small \begin{align} \hat L^2&=-\frac{\hbar^2}{\sin\theta}\frac{\partial }{\partial \theta}\left(\sin{\theta}\frac{\partial }{\partial \theta}\right)-\frac{\hbar^2}{\sin^2\theta}\frac{\partial ^2}{\partial \varphi^2}\\ &=-\hbar^2\left[\frac{1}{\sin\theta}\frac{\partial }{\partial \theta}\left(\sin\theta\frac{\partial }{\partial \theta}\right)+\cot^2\theta \frac{\partial^2 }{\partial \varphi^2}\right]-\hbar^2\frac{\partial^2 }{\partial \varphi^2}\\ &=\left(\hat L_x^2+\hat L_y^2\right)+\hat L_z^2 \end{align} \quad{\scriptsize (式20.3)}$
而同样是在第19课中,我们又通过上面的分解知道,角动量的$ \small z $分量$ \small \hat L_z $与哈密顿算符也是相互对易的,哈密顿算符的本征态也是$ \small \hat L_z $的本征态。
这样,对于薛定谔方程的某个解$ \small \left|\psi\right> $,它也应该同时满足$ \small \hat L_z $的本征方程,我们不妨将这个方程写为:
$\small \hat L_z\left|\psi\right>=L_{z,m}\left|\psi\right> \quad{\scriptsize (式20.4)}$
(其中$ \small m $为本征值的序号)
如果我们在球坐标表象下将它具体写出来,就是:
$\small -\text i\hbar\frac{\partial \psi}{\partial \varphi}=L_{z,m}\psi \quad{\scriptsize (式20.5)}$
这就是我们一开始要找到的那个“软柿子”。
我们看到,它其实只有对$ \small\varphi $求导的项,所以本质上其实是一个常微分方程,而这也正是我们第一步要求解的对象。
它的解我们很容易想到,就是指数函数:
$\small \psi=A\text e^{-\frac{L_{z,m}}{\text i\hbar}\varphi} \quad{\scriptsize (式20.6)}$
而其中的积分常数$ \small A $应该还和另外两个变量$ \small r,\theta $有关,因此解的形式也可以写为:
$\small \psi=A(r,\theta)\text e^{-\frac{L_{z,m}}{\text i\hbar}\varphi} \quad{\scriptsize (式20.7)}$
这里我们相当于得到了能量本征函数$ \small \psi $中与$ \small \varphi $有关的部分,同时得到了本征值$ \small L_{z,m} $。
当然,$ \small L_{z,m} $的取值还和具体的边界条件有关,我们稍后再讨论,但现在我们至少可以将它看作一个常数。
在这个基础上,我们继续讨论第二步的求解对象:
如果对$ \small \psi $求两次$ \small \varphi $的偏导,我们会得到:
$\small \frac{\partial^2 \psi}{\partial \varphi^2}=-\frac{L_{z,m}^2}{\hbar^2}\psi \quad{\scriptsize (式20.8)}$
将这个关系代入$ \small \hat L^2 $的球坐标表象中,我们会将它变成:
$\small \begin{align} \hat L^2&=-\frac{\hbar^2}{\sin\theta}\frac{\partial }{\partial \theta}\left(\sin{\theta}\frac{\partial }{\partial \theta}\right)-\frac{L_{z,m}^2}{\sin^2\theta} \end{align} \quad{\scriptsize (式20.9)}$
再代入$ \small \hat L^2 $的本征方程(式20.2),我们就得到:
$\small \begin{align} \left[-\frac{\hbar^2}{\sin\theta}\frac{\partial }{\partial \theta}\left(\sin{\theta}\frac{\partial }{\partial \theta}\right)-\frac{L_{z,m}^2}{\sin^2\theta}\right]\psi &=\lambda \psi \end{align} \quad{\scriptsize (式20.10)}$
这里,由于原来对$ \small \varphi $求导的项已经化为了常数$ \small L_{z,m}^2 $,因此这个方程也只包含一个变量$ \small \theta $,这就是第二步要求解的常微分方程。
这个方程的解比较复杂,我们也将它的具体形式放到后面介绍,现在姑且将它记为$ \small \varTheta_\lambda(\theta) $,于是能量本征函数可以写成$ \small \varTheta_\lambda(\theta) $乘以一个只与$ \small r,\varphi $有关的函数(对于变量$ \small \theta $而言就相当于积分常数):
$\small \psi=B(r,\varphi)\varTheta_\lambda(\theta) \quad{\scriptsize (式20.11)}$
而与$ \small \varphi $有关的部分我们前面已经给出(式20.7),因此能量本征态其实可以写成三个单变量函数的乘积:
$\small \begin{align} \psi&=R(r)\varTheta_\lambda(\theta)\text e^{-\frac{L_{z,m}}{\text i\hbar}\varphi} \end{align} \quad{\scriptsize (式20.12)}$
接下来,我们就来到了最后一场战役:求解最后的未知函数$ \small R(r)$
我们将$ \small \hat L^2 $的本征值$ \small \lambda$ (式20.10右边)作为已知条件代入总的薛定谔方程中,就得到:
$\small -\frac{\hbar^2}{2m_e}\left[\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial }{\partial r}\right)+\frac{\lambda}{r^2}\right]\psi+V(r)\psi=E\psi \quad{\scriptsize (式20.13)}$
这样,包含$ \small \theta,\varphi $的算符都被消去,万般愁绪皆化为常数$ \small \lambda $,我们也就只剩下了一个关于$ \small r $的常微分方程。
求解了它,也就求得了最后的未知函数$ \small R_n(r) $,以及能级的取值范围$ \small E_n$
而完成这一切以后,能量本征函数就可以由三部分解组合成这样的形式:
$\small \psi=R_n(r)\varTheta_\lambda(\theta)\varPhi_m(\varphi) \quad{\scriptsize (式20.14)}$
(其中 $ \small \varPhi_m(\varphi)=\text e^{-\frac{L{z,m}}{\text i\hbar}\varphi} $ 是我们已知的)
这个形式有一个通用的名称,就是我们经常在求解偏微分方程时用到的所谓“分离变量解”。
(一本正经的量子力学书通常都是一上来先告诉我们,本征函数可以写成这样的分离变量形式,因为这对搞物理的人来说可以看作常识,但我们是一群业余爱好者或者初学者,所以我们用这种更自然的思路得到了它)
它的代数意义,其实就是几个相互对易的算符各自的本征态的直积,这个直积形成了这些算符的共同本征态。
(同学们不用去管什么是直积,这里先理解为函数的简单相乘就行了,有兴趣进一步了解算符和向量直积运算的同学,可以去读喀兴林老先生的高量教材[1] )
在我们这个例子里,这个分离变量解对应的三个对易算符就是:
$\small \matrix{\psi=&R_n(r)&\varTheta_\lambda(\theta)&\varPhi_m(\varphi)\\ &\downarrow&\downarrow&\downarrow\\ &\frac{\hat p_r^2}{2m_e}+\hat V&\hat L_x^2+\hat L_y^2&\hat L_z } \quad{\scriptsize (式20.15)}$
这就是我们的整个求解思路。
这里顺便说一句,有兴趣的同学们可以利用这个思路,去尝试求解一下我们第17课给出的三维无限深势阱模型,当时我们是直接给出解的,现在同学们可以有清晰的思路去还原求解过程了。
接下来,我们来具体看看分离变量解中各个本征函数的具体形式,以及相应的各个本征值$ \small L_{z,m},\ \lambda,\ E_n $的具体取值范围。
我们先从更具一般性的角向解开始。
2) 角向解
方程的角向解是非常值得玩味的。
我们首先来解决最简单的$ \small \hat L_z $的本征方程:
$\small -\text i\hbar\frac{\text d \varPhi_m}{\text d \varphi}=L_{z,m}\varPhi_m \quad{\scriptsize (式20.16)}$
(分离变量解中的其他函数$ \small R(r)\varTheta(\theta) $可以视为积分常数省略)
前面我们已经知道,它的解就是指数函数:
$\small \varPhi_m(\varphi)=\text e^{-\frac{L_{z,m}}{\text i\hbar}\varphi} \quad{\scriptsize (式20.17)}$
现在我们来确定本征值$ \small L_{z,m}$
我们知道,由于经度$ \small \varphi $对应的是绕$ \small z $轴的旋转,因此它的函数$ \small \varPhi_m(\varphi) $具有一个天然的周期性:
$\small \text e^{-\frac{L_{z,m}}{\text i\hbar}\varphi}=\text e^{-\frac{L_{z,m}}{\text i\hbar}\left(\varphi+2\pi\right)}=\text e^{-\frac{L_{z,m}}{\text i\hbar}\varphi}\text e^{-\frac{L_{z,m}}{\text i\hbar}2\pi} \quad{\scriptsize (式20.18)}$
于是我们得到:
$\small \text e^{-\frac{L_{z,m}}{\text i\hbar}2\pi}=1 \quad{\scriptsize (式20.19)}$
也就是:
$\small -\frac{L_{z,m}}{\text i\hbar}=\text im\quad (m\in\mathbb{Z}) \quad{\scriptsize (式20.20)}$
这样我们就得到了$ \small \hat L_z $的本征值的取值范围:
$\small L_{z,m}=m\hbar\quad (m\in\mathbb{Z}) \quad{\scriptsize (式20.21)}$
以及相应的本征函数:
$\small \varPhi_m(\varphi)=\text e^{-\text im\varphi}\quad (m\in\mathbb{Z}) \quad{\scriptsize (式20.22)}$
我们将$ \small m $称作“磁量子数”,因为它对应着能级在磁场中的表现,关于这个的讨论我们以后还会展开。
不过这里其实还有一个细节问题,就是$ \small m $的取值范围。
虽然理论上$ \small m $可以取任意整数,但是稍后我们会看到,当我们将$ \small \hat L_z $当作$ \small \hat L^2 $的一部分看待时,$ \small m $的取值其实是有上下限的,这个上下限取决于$ \small L^2 $的大小(同学们可以提前想想为什么,这个用经典力学中的关系就能想到)。
现在,我们将$ \small L_{z,m}=m\hbar $代入$ \small \hat L^2 $的本征方程,去求解分离变量解中的第二个函数:
$\small \begin{align} \left[-\frac{\hbar^2}{\sin\theta}\frac{\text d }{\text d \theta}\left(\sin{\theta}\frac{\text d }{\text d \theta}\right)-\frac{m^2\hbar^2}{\sin^2\theta}\right]\varTheta &=\lambda \varTheta \end{align} \quad{\scriptsize (式20.23)}$
(照例省略分离变量解中与 $\small \theta $无关的部分)
这个方程看起来不太好惹的样子,但好在我们可以去搬救兵。
实际上,经典物理时代的先辈们已经为这一类微分方程准备好了标准解,我们这里直接给出答案:
它是一个多项式形式的特殊函数序列,名叫缔合勒让德函数(Associated Legendre Functions$,$也翻译成连带勒让德函数),它的形式看起来有点复杂[2]:
$\small \text P_{lm}(\cos\theta)=\frac{1}{2^l\cdot l!}\left(1-\cos^2\theta\right)^{\frac{m}{2}}\frac{\text d^{l+m}}{\text d(\cos\theta)^{l+m}}\left(\cos^2\theta-1\right)^l \quad{\scriptsize (式20.24)}$
$($其中$ \small l=0,1,2,\cdots )$
而在讨论方程解的性质的时候,我们通常会将它与关于$ \small \varphi $的解$ \small \varPhi(\varphi) $合写到一起,并且加上系数,记为:
$\small Y_{lm}(\theta,\varphi)=\sqrt{\frac{(l-m)!}{(l+m)!}\frac{2l+1}{4\pi}}\text P_{lm}(\cos\theta)\text e^{\text im\varphi} \quad{\scriptsize (式20.25)}$
这个函数名叫球谐函数(Spherical Harmonics),也是一种特殊函数,从名字可以看出它和球对称问题的渊源。
如果将球坐标表象下的角动量平方算符作用在球谐函数上,我们就会得到这样的关系式:
$\small \begin{align} \left[-\frac{\hbar^2}{\sin\theta}\frac{\partial }{\partial \theta}\left(\sin{\theta}\frac{\partial }{\partial \theta}\right)-\frac{m^2\hbar^2}{\sin^2\theta}\right]Y_{lm} &=l(l+1)\hbar^2 Y_{lm} \end{align} \quad{\scriptsize (式20.26)}$
这样,角动量平方的本征值就显现出来了:
$\small \lambda=l(l+1)\hbar^2=l^2\hbar^2+l\hbar^2 \quad{\scriptsize (式20.27)}$
我们将$ \small l $称作“角量子数”,它可以看成角动量平方$ \small \hat L^2 $的本征值的序号。
接下来,我们似乎就应该将这个值代入关于$ \small r $的径向方程中,去求解径向函数$ \small R(r) $了……
但是等一等:同学们看到$ \small \hat L^2 $的本征值的时候,是不是觉得很别扭?
根据我们的直觉,角动量平方量子化以后,似乎应该也等于某个整数的平方、也就是类似于$ \small \lambda=l^2\hbar^2 $这种看起来很干净的形式,但是这里居然多出来了一项看起来很讨厌的$ \small l\hbar^2 $,这是个什么情况?
这里就是角向解最值得玩味的地方了。
接下来我们就来具体说一说。
3) 角动量本征值的物理意义
简单地说,角动量本征值中看似多余的$ \small l\hbar^2 $这一项,来源于不确定性。
还记得第18课讨论球坐标薛定谔方程意义的时候,我们刻意地将角动量平方分解成两部分:
$\small L^2=\left(L_x^2+L_y^2\right)+L_z^2 \quad{\scriptsize (式20.28)}$
这首先意味着,总的角动量平方一定不小于$ \small L_z^2 $的平方,即:
$\small L^2=\left(L_x^2+L_y^2\right)+L_z^2\geq L_z^2=m^2\hbar^2 \quad{\scriptsize (式20.29)}$
换句话说,就是$ \small m^2 $会有一个上限值,这也就是前面我们提到过的$ \small m $的取值范围问题了。
而现在我们要回答的问题是:$ \small L_z^2 $的最大值是不是就等于$ \small L^2 $?
在经典力学中的确是这样,因为当角动量方向正好是$ \small z $方向的时候,就有$ \small L_z^2=L^2$
但是量子力学当中会怎样呢?
我们先从数学的角度来找到$ \small m $的取值范围。
如果仔细观察连带勒让德函数,我们会发现,如果将最后一项$ \small \left(\cos^2\theta-1\right)^l $展开,那么其中的最高次项为$ \small \cos^{2l}\theta $,而这一项前面有一个求导运算$ \scriptsize \frac{\text d^{l+m}}{\text d(\cos\theta)^{l+m}} $,这将帮助我们找到$ \small m $的上下限:
当$ \small m<-l $的时候,求导运算没有意义;当$ \small m>l $的时候,$ \scriptsize \frac{\text d^{l+m}}{\text d(\cos\theta)^{l+m}} $对$ \small \left(\cos^2\theta-1\right)^l $求导结果为0(因为此时最高次项 $\small 2l<m+l )$,导致整个连带勒让德函数变为0
所以,要让整个勒让德函数有意义,$ \small m $的取值范围就只能是:
$\small m=0,\pm 1,\pm 2,\cdots,\pm l \quad{\scriptsize (式20.30)}$
(如果同学们去读一本正经的量子力学教材,还会看到利用所谓升降算符:$ \small \hat L_{\pm}=\hat L_x\pm \text i\hat L_y $来处理$ \small m $取值上下限的抽象方法,计算起来更加简单明了,但我们这里限于篇幅暂时不展开,等我们讨论对称性的时候再来详聊)
于是,我们发现:
$\small \max_m{L_{z,m}^2}=l^2\hbar^2{<}l^2\hbar^2+l\hbar^2=L^2 \quad{\scriptsize (式20.31)}$
有了这个关系,我们就能回头讨论$ \small L^2 $本征值中多出来的$ \small l\hbar^2 $那一项了。
现在,请先回忆起我们在第19课中讨论过的两组对易关系以及它们的物理意义:
一是三个角动量分量算符的对易关系:
$\small \begin{cases} \left[\hat L_x,\hat L_y\right]=\text i\hbar\hat L_z\\ \left[\hat L_y,\hat L_z\right]=\text i\hbar\hat L_x\\ \left[\hat L_z,\hat L_x\right]=\text i\hbar\hat L_y \end{cases} \quad{\scriptsize (式19.17)}$
二是$ \small \hat L_x^2+\hat L_y^2 $和$ \small \hat L_z^2 $之间的对易关系:
$\small \begin{align} \left[\hat L_x^2+\hat L_y^2,\hat L_z^2\right]&=0 \end{align} \quad{\scriptsize (式19.18)}$
当时我们提到,三个角动量算符$ \small \hat L_x,\hat L_y,\hat L_z $相互不对易,这意味着三个角动量不能同时具有确定的值,或者说角动量矢量没有确定的方向。
而$ \small \hat L_x^2+\hat L_y^2 $和$ \small \hat L_z^2 $相互对易,又告诉我们:
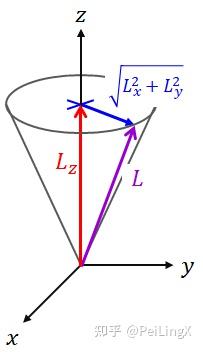
当$ \small \hat L_z $处于它的本征态、即$ \small L_z $具有确定值时,虽然$ \small L_x,L_y $单独看都不确定,但它们的平方和$ \small L_x^2+L_y^2 $是确定的。此时,角动量矢量的可能取值就形成了一个高为$ \small L_z $、底面半径为$ \small \sqrt{L_x^2+L_y^2} $的圆锥面。
这意味着,量子力学中不会像经典力学那样、出现角动量矢量确定地处于$ \small z $方向的情形,于是也就不会出现$ \small L_z^2=L^2 $的情形。
而在量子版的角动量形成的“圆锥面”上,我们可以很容易看出,当$ \small L_z^2 $取最大值$ \small l^2\hbar^2 $的时候,$ \small L^2 $相对于$ \small L_z^2 $多出来的$ \small l\hbar^2 $,其实就是圆锥的底面半径平方:$ \small L_x^2+L_y^2$
说到底,这个多出来的$ \small l\hbar^2 $,其实就是$ \small \hat L_x,\hat L_y $的不确定性造成的。
这个看似反常的结果又一次为我们展示了不确定性在量子世界中无处不在的影子。
当然,我们也不难看到,当$ \small l\rightarrow \infty $时,$ \small l^2\gg l $,此时$ \small L^2 $中的$ \small L_x^2+L_y^2 $分量就可以忽略,有:
$\small \max_m L_{z,m}^2\simeq L^2 \quad{\scriptsize (式20.32)}$
这就回到了经典力学中的结果,也再一次暗合了玻尔的对应原理。
顺便说一句,在这个讨论过程中我们还发现,对于同一个$ \small L^2 $本征值,我们可以取不同的$ \small m $值(对应着不同的$ \small \hat L_x^2+\hat L_y^2 $和$ \small \hat L_z^2 $的组合),这意味着$ \small L^2 $是简并的,根据$ \small m $的取值范围可知简并度是$ \small 2l+1$
这个简并背后蕴含着非常值得玩味的对称性,我们说完氢原子方程解后会对它做一个简单介绍,而在未来正式讨论对称性的时候还会将它作为典型案例来详细讨论。
现在解释清楚了$ \small L^2 $本征值看似反常的项,我们就可以了无牵挂地进入最后一个环节:求解径向函数$ \small R(r)$
不过,读到这里,想必同学们也有些疲乏了,因此这件事情我们放到下节课来做。
4) 总结与预告
这节课里,我们先梳理了氢原子薛定谔方程的求解思路:
通过$ \small \hat H,\hat L^2,\hat L_z $相互对易、具有共同本征态的特点,以及它们的层层套娃[3]的关系$(\small \hat H $包含$ \small \hat L^2 $、$ \small \hat L^2 $包含$ \small \hat L_z$),将它们分化瓦解成三层不同的方程。
然后,我们从信息量最少、也是最简单的$ \small \hat L_z $的本征方程(简单是因为它只与$ \small \varphi $有关)入手,将方程中的$ \small \hat L_z $算符化为常数(即本征值),并且得到薛定谔方程解中与$ \small \varphi $有关的部分$( \small \hat L_z $的本征函数);
将$ \small \hat L_z $的本征值和本征函数“套娃”装进$ \small \hat L^2 $的本征方程中,我们就可以将这个方程化为关于$ \small \theta $的常微分方程,也就能求出$ \small \hat L^2 $的本征值和本征函数(薛定谔方程解中与$ \small \theta,\varphi $有关的部分);
再将$ \small \hat L^2 $的本征值和本征函数“套娃”装进$ \small \hat H $的本征方程、也就是整个氢原子薛定谔方程中,我们就能将方程化为关于$ \small r $的常微分方程,求出方程解的径向部分,并且得到整个能量本征值和本征函数。
这个过程体现在微分方程中,就是求解线性偏微分方程常用的分离变量法。
而在本课的后半部分,我们解决了的$ \small \hat L_z,\hat L^2 $的本征方程,得到了方程的角向解:
$- \small \hat L_z $的本征值为$ \small m\hbar $,其中$ \small m $的取值范围为:
$\small m=0,\pm 1,\pm 2,\cdots,\pm l$
而本征函数为复指数函数:
$\small \varPhi_m(\varphi)=\text e^{-\text im\varphi}$
$- \small \hat L^2 $的本征值为$ \small l(l+1)\hbar^2 $,其中$ \small l $是整数(它的取值范围我们将在下节课结合能量本征值一起讨论)
而本征函数为球谐函数:
$\small Y_{lm}(\theta,\varphi)=\sqrt{\frac{(l-m)!}{(l+m)!}\frac{2l+1}{4\pi}}\text P_{lm}(\cos\theta)\text e^{\text im\varphi}$
在这个过程中,我们发现,对比经典力学以及玻尔的氢原子模型,$ \small \hat L^2 $的本征值有些反常。
具体来说就是:当$ \small \hat L_z $的本征值取最大值$ \small \max (m)\hbar=l\hbar $时,总的角动量平方仍然比$ \small L_z^2=l^2\hbar^2 $多出了一个$ \small l\hbar^2 $项。
而结合我们上节课中对$ \small \hat L_x,\hat L_y,\hat L_z $互不对易的性质的认识,我们发现,这个看似反常和多余的部分,正是来自于$ \small \hat L_z $确定时$ \small \hat L_x,\hat L_y $的各自的不确定性。
但另一方面,$ \small \hat L_x^2+\hat L_y^2 $与$ \small \hat L_z^2 $相互对易的性质又告诉我们,$ \small \hat L_z $确定时,角动量$ \small \hat {\boldsymbol L} $的可能取值会形成一个圆锥面,前面那个反常的$ \small l\hbar^2 $项,正好就是这个圆锥的“底面半径”平方,即$ \small \hat L_x^2+\hat L_y^2 $,这是一个确定的值。

这其中蕴含的确定和不确定的关系,非常值得玩味。
到这里,我们就完成了与氢原子方程角向解的初次见面。
这里顺便说一句,对于球对称模型而言,角向本征方程与径向坐标$ \small r $无关,也就与势能函数$ \small V(r) $无关(这也是径向函数与角向函数可以分离变量的基础),所以我们得到的角向解不仅仅适用于氢原子,也适用于一切球对称模型。
而唯一与$ \small r $有关的,自然就是径向解了。下节课,我们就来求出氢原子方程的径向解,并且求出整个能量本征值和本征方程。
参考
- 喀兴林,《高等量子力学(第二版)》,第55~57页介绍了向量和矩阵的直积运算,第90~93页介绍了三维算符和本征态的直积分解,两部分内容结合起来看,并且动手进行一些计算,你会对分离变量解的直积意义产生非常深刻的体会。
- 回字有四种……啊不对,连带勒让德函数有多种写法,这里采用的是张永德《量子力学》书中的写法,详见该书第86页
- 所以封面图没有放氢原子模型,而是放了套娃,因为它更能形象展示氢原子薛定谔方程求解过程
编辑于 2022-03-16 14:21
