fmingde
版次: 2024
了解本系列其他文章,请浏览目录:
《大学物理》内容提要目录
§11波动光学(干涉)
〇、可见光
波长范围:$400 \,\rm nm \sim 760\,\rm nm$ (紫色~红色)
$400 \,\rm nm$对应紫光,$760\,\rm nm$对应红光,绿光在$600\,\rm nm$附近
玻璃折射率 $n=1.5$
一、相干光
1. 相干光条件
多列光波的)频率相同,振动方向相同,相位相同或相位差恒定。
2. 光程和光程差
光通过的几何路程与介质折射率之积$nr$ ,称为光程。
光程 $nr$等于在相同的时间内光在真空中传播的几何路程。
(采用光程后,相当于将不同介质中的路程都换算为相同时间内在真空中的传播路程,简化相位、相位差等的运算)。
光程差:两束光的光程之差
相位差与光程差的关系:$\Delta\varphi=2\pi\cfrac \Delta \lambda$ ,其中 $\lambda$为真空中光的波长。
3. 干涉加强和减弱的条件(明暗纹条件)
$\Delta=\left\{ \begin{array}{l}
\pm2k\cfrac \lambda 2 & \text{干涉加强(明纹)}\\ \pm(2k+1)\cfrac \lambda 2 & \text{干涉减弱(暗纹)} \end{array} \right.$
$(k=0,1,2,\ldots)$
$\Delta$: 两相遇两光线的光程差
在不同的干涉装置中, $\Delta$的计算式不同
二、获得相干光的方法及典型干涉现象
1. 杨氏双缝干涉(分波阵面法获得相干光)
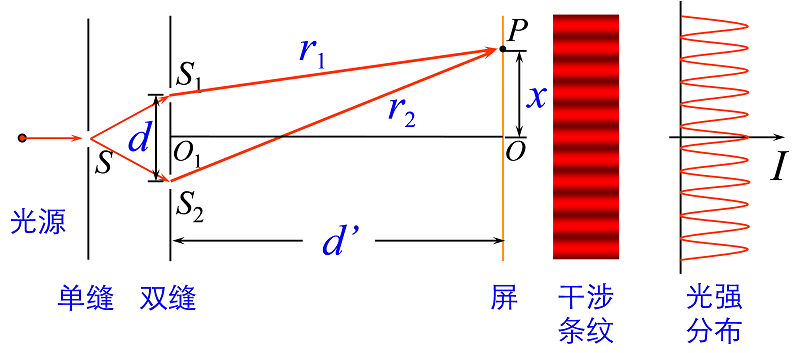
(1)明暗纹条件
$\Delta =d\sin\theta\approx \cfrac d {d'}x=\left\{ \begin{array}{l}
\pm k \lambda & \text{明纹} \\ \pm(2k+1)\cfrac \lambda 2 & \text{暗纹} \end{array} \right.$
( $k=0,1,\ldots$ $d$:双缝间距 $d'$:缝屏间距)
(2)条纹位置
$x=\left \{ \begin{array}{l}\pm k \cfrac {d'} d \lambda & \text{明纹} \\ \pm (2k+1)\cfrac {d'} {d} \cfrac \lambda 2 &\text{暗纹}\end{array} \right.$
明暗相间的等间距的直条纹。
(3)条纹间距:$\Delta x=\cfrac {d'} d\lambda$
备注:以上关系,默认传播路径的折射率为$1$(空气)。
若传播路径上的折射率为$n$,则 ,$\Delta =nd\sin\theta\approx\cfrac {nd} {d'} x$ $\Delta x=\cfrac {d'}{nd} \lambda$ ($d$替换为$nd$)
计算要求:★1)条纹位置、间距,波长等计算;2)改变介质后条纹位置的变化
典型习题:三、1, 2(1);三、2(2)
2. 薄膜干涉(分振幅法获得相干光)
(1)一般情况
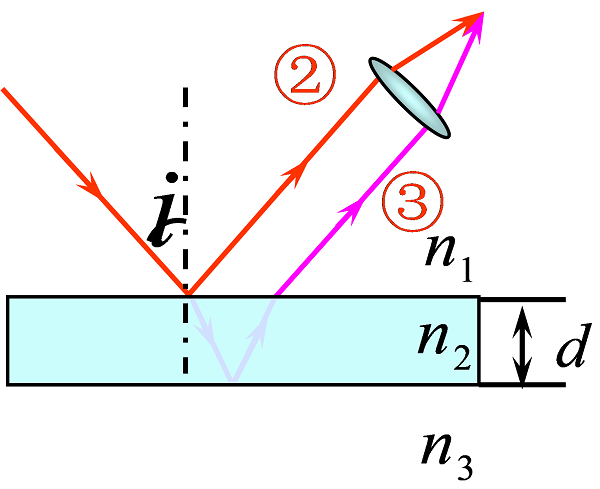
1)明暗纹条件:
$\begin{align} \Delta & =2d\sqrt{n_2^2-n_1^2\sin^2i}+\Delta'\\& =\left \{ \begin{array}{l} k\lambda &k=1,2,3,\ldots & \text{明纹}\\(2k+1)\cfrac \lambda 2 &k=1,2,3,\ldots &\text{暗纹} \end{array} \right.\end{align}$
$\Delta'$: 附加光程差,需判断上、下表面的半波损失。
2)半波损失:光从光疏介质(折射率小)入射到光密介质(折射率大)表面时,反射光线的相位较之入射光线的相位跃变了$\pi$ (即光程差增加了$\cfrac \lambda 2$ )
3)$\Delta'$快速判断规则:
$\Delta '=\left \{ \begin{array}{l} 0 &n_1<n_2<n_3 & (\text{或}n_1>n_2>n_3)\\ \cfrac \lambda 2 &n_1<n_2>n_3 & (\text{或}n_1>n_2<n_3) \end{array} \right.$
(2)等倾干涉条纹(薄膜厚度均匀)
同心圆环。同一条纹是来自同一倾角的入射光形成的。反射光的干涉图样与透射光的干涉图样是互补的。
(3)等厚干涉条纹(光线垂直入射)
1)明暗纹条件
$\Delta =2dn+\Delta'=\left \{ \begin{array}{l} k\lambda &k=1,2,3,\ldots & \text{明纹}\\(2k+1)\cfrac \lambda 2 &k=1,2,3,\ldots &\text{暗纹} \end{array} \right.$
厚度相同处,光程差相同,形成同一条纹
相邻明(暗)纹间的厚度差: $\Delta d=\cfrac \lambda {2n}=\cfrac {\lambda_n } {2}$
2)劈尖: 两平板透明介质(如玻璃)的一端棱边接触而形成的夹角很小的器件。主要关注两透明介质之间的劈形区域,讨论垂直入射光在其上下表面反射时形成的干涉现象。
劈尖装置的干涉条纹为明暗相间的等间距的与棱边平行的直条纹。
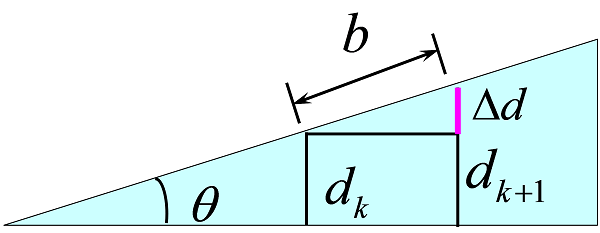
条纹间距: $b=\cfrac \lambda {2n\sin\theta}\approx\cfrac \lambda {2n\theta}$
(图中小三角形,高为$\cfrac {\lambda_n} 2=\cfrac \lambda {2n}=b\sin\theta$ )
3)牛顿环:牛顿环干涉装置形成的干涉图样
干涉装置:平凸透镜和平板玻璃叠合,形成不均匀空气薄膜。
干涉图样:内疏外密的同心圆环。
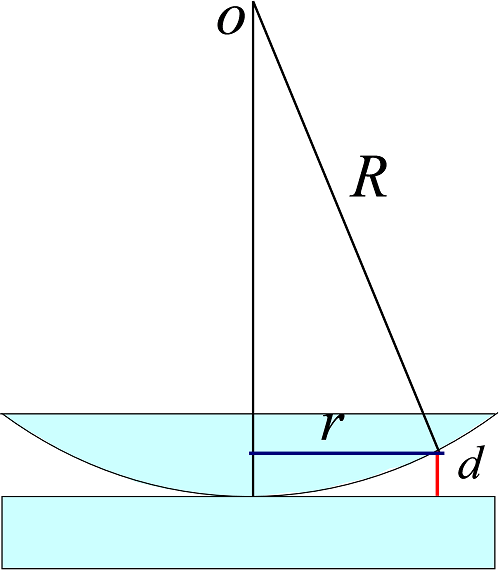
薄膜厚度$d$与牛顿环半径$r$关系:$d\approx\cfrac {r^2} {2R}$ , 是平凸透镜凸面的曲率半径。
牛顿环半径:$r=\begin{cases} \sqrt{\cfrac {(2k-1)R\lambda }{2n}} & k=1,2,\ldots(\text{明纹}) \\ \sqrt{\cfrac {kR \lambda}{n}} & k=0,1,\ldots (\text{暗纹})\end{cases}$
$n$为胞膜的折射率,通常为1(空气)。
主要掌握$d\approx\cfrac {r^2} {2R}$ , 牛顿环半径可再由"3)"中明暗纹条件推出。
(4)迈克耳孙干涉仪
动镜移动距离与条纹移动数的关系:$d=N\cfrac \lambda 2$
光线在动镜处往返,光程变化是镜片移动距离的两倍。 动镜每移动半个波长,两干涉光路之间光程差变化 ,对应一个级次条纹变化。
计算要求:★★1)干涉结果、厚度、波长的计算;2)劈尖角度计算
典型习题:三、3;三、5 光学综合练习:三、1
3. 相干长度
由于实际的“单色”光源的波长不可能是完全的单一波长(具有一定的波长范围),两光线若光程差大过一定长度之后,不同波长成分的干涉现象互相混叠,最终表现为观察不到干涉现象。这一极限长度称为相干长度。
例如:一般的玻璃片(毫米级)上下表面反射光之间观察不到干涉现象,因为玻璃片厚度超过了相干长度。
另,在劈尖、牛顿环等实验的讨论中,只关心两玻璃片之间,极薄的空气层(微米级)上下表面的反射光的干涉,而不关心玻璃片本身上下表面的反射光,原因就是因为实验室中实际采用的玻璃片厚度将大于相干长度。
§11波动光学(衍射)
一、衍射的基本原理
1. 惠更斯—菲涅耳原理
波阵面上各点都可当作子波波源,其后波场中各点处的波的强度由个子波在该点的相干叠加决定。
2. 衍射的分类
1)菲涅耳衍射:近场衍射,计算理论复杂,暂不学习。
2)夫琅和费衍射:远场衍射,光源和成像处均很远,近似为平行光线会聚成像。在实验室中,借助透镜将平行光会聚到观察屏上成像。
二、单缝夫琅和费衍射
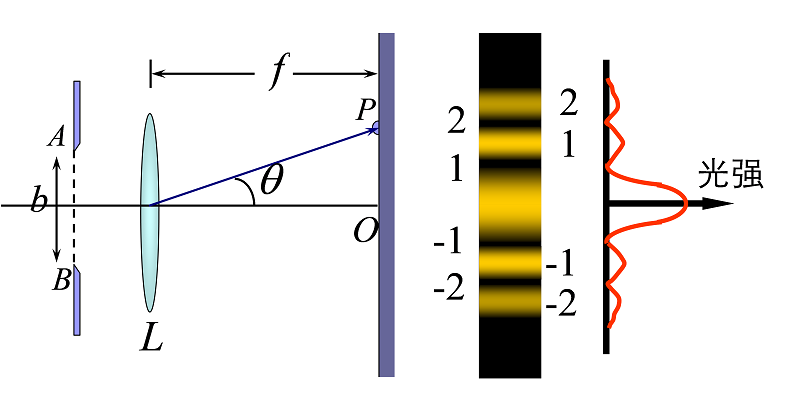
1. 条纹规律分析方法:半波带法

将两边缘光线的光程差 $b\sin\theta$ (右图$BC$段),按半波长分割,并过等分点作$AC$平行线,将缝$AB$分成若干条带,其中的完整条带称为半波带。
相邻半波带的以角度$\theta$出射的平行光,在成像屏上会聚时,干涉相消。
当能划分的半波带数目是偶数个时,两两干涉相消,为暗纹。当能划分的半波带数目是奇数个时,两两相消后余一个,为明纹。
2. 明暗纹条件
$\begin{cases} \theta=0 \quad \quad \text{中央明纹} \\ b\sin\theta=\begin{cases} \pm2k \cfrac \lambda 2 & \text{暗纹}\\ \pm(2k+1)\cfrac \lambda 2 & \text{明纹} \end{cases}\end{cases} $
$(k=1,2,\ldots)$
3. 条纹位置: $x=f\tan\theta$
1)借助透镜成像,条纹位置与缝位置无关
2)衍射角很小时,$\tan \theta\approx\sin \theta\approx\theta$ 。衍射角一般很小。
两条纹间距,$\Delta x=f(\tan \theta_1-\tan \theta_2)\approx f\Delta \theta$ 。
3)多种波长入射时,条纹的位置关系(如是否重合),可通过比较衍射角$\theta$ 得知。
4)衍射角最大取到 $\pm\cfrac \pi 2$
4. 中央明纹宽度:$l_0=\cfrac {2\lambda f}{b}$
为1级暗纹位置乘以2
$l_0=2x_1=2f\tan\theta_1=2f\sin\theta_1=2f\cfrac \lambda b$
计算要求:★★ 1)条纹分布、波长、缝宽的计算; 2)条纹重合问题 重合: 衍射角相同
典型习题:三、2;三、3
三、圆孔夫琅和费衍射
爱里斑半角宽度: $\theta_0=1.22\cfrac \lambda D$
光学仪器的最小分辨角: $\theta_0=1.22\cfrac \lambda D$
光学仪器的分辨本领: $\cfrac 1 {\theta_0}=\cfrac D {1.22\lambda}$
由最小分辨角计算最小分辨间距时,按“弧长$s$=半径$r×$张角”计算: $s\approx r\theta_0$
计算要求:★最小分辨角度、最小分辨距离的计算
典型习题:三、4
三、光栅衍射
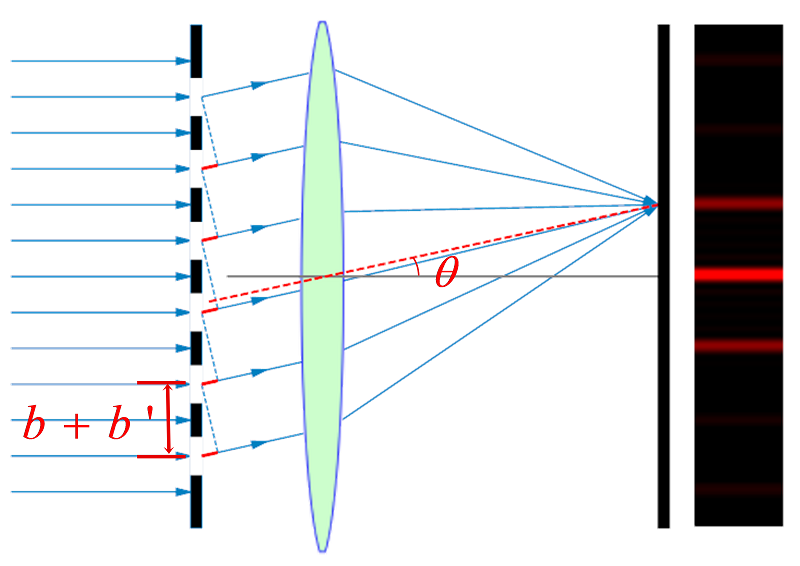
1. 衍射图样的特点
细而明亮的条纹;缝数越多,条纹越细且明亮;
条纹位置由多光束干涉决定,条纹亮度由单缝衍射决定。
有缺级现象。
2. (光垂直照射时的)光栅方程
$(b+b')\sin\theta=\pm k \lambda, \quad\quad k=0,1,2,\ldots $
给出了各(主)明纹的位置(衍射角)
式中:$b$ :缝宽度,$b'$ :缝间不透光部分宽度
$b+b'=d$:光栅常数, $\theta$:衍射角
3. 光斜入射时的光栅方程
$(b+b')(\sin\theta+\sin\phi)=\pm k \lambda, \quad\quad k=0,1,2,\ldots $
4. 屏上条纹位置:$x=f\tan\theta $
备注事项与单缝衍射相同。
如:小角度时,$\tan\theta\approx\sin\theta\approx\theta$
5. 缺级
条件: 光栅常数是缝宽的整数倍
缺级级次: $k=\cfrac {b+b'}{b} k' \quad \quad k'=\pm1,\pm2,\ldots$
计算要求:★★★1)条纹位置、波长、光栅常数的计算;2)$n$级出现缺级,则一般$\cfrac {b+b'}{b}=n$;3)条纹数目,令$\theta =90 ° $,求出$k_{max}$
典型习题:三、6;光学综合练习:三、3
四、X射线衍射
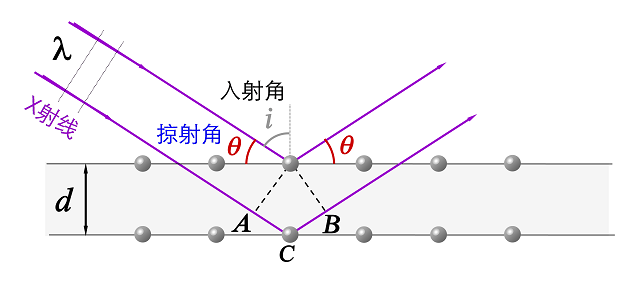
晶体的点阵结构可看成三维光栅,能使波长极短的X射线产生衍射,其衍射极大值满足:
布拉格方程 $2d\sin\theta=k\lambda\quad\quad k=1,2,\ldots$
$\theta $为入射方向与原子层面间夹角(掠射角)
§11 波动光学(偏振)
一、光的偏振态
从偏振情况,光可分为自然光、线偏振光、部分偏振光、椭圆偏振光和圆偏振光。
线偏振光: 光矢量始终沿某一方向振动
![]()
自然光可以看作是由两个相互独立,振幅相同,振动方向垂直的线偏振光的叠加。
![]()
二、起偏和检偏
1. 起偏
自然光起偏得到线偏振光
光强变化: $I=\cfrac {I_0} 2$
$I_0$为入射光光强
三种起偏方法:偏振片起偏(利用晶体的二向色性)、反射起偏(利用玻璃堆的反射)、双折射起偏(利用尼科尔棱镜)。
起偏器件具有确定的透振方向,画图时,用双箭头标识。
2. 检偏
线偏片通过偏振片后,成为振动方向与偏振片透振方向相同的线偏振光。
光强变化遵从马吕斯定律 $I=I_0\cos^2\alpha$
$\alpha$为入射线偏振光振动方向与偏振片透振方向的夹角
计算要求:★★偏振片组合后的光强计算
典型习题:三、1,2
三、反射光和折射光的偏振
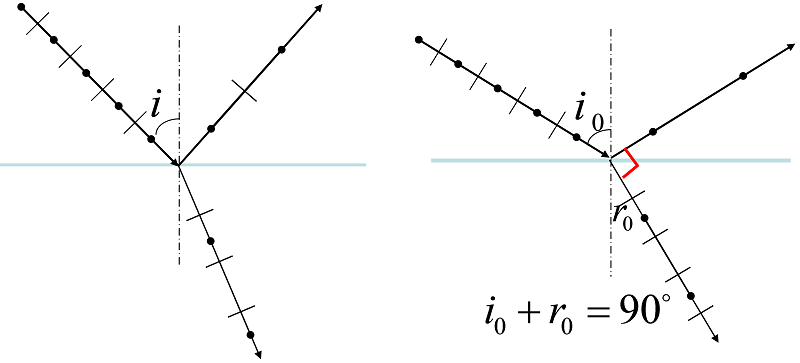
在反射、折射现象中,界面对两种振动成分(垂直入射面的振动和平行入射面的振动)的反射、折射比例不同,导致反射、折射光线成为部分偏振光。反射光线中,垂直入射面的振动占强,折射光线中,平行入射面的振动占强。
当反射光等于起偏角$i_0$时,反射光中,平行入射面的振动完全消失,成为振动方向垂直于入射面的线偏振光,折射光为以平行于入射面的光振动为主的部分偏振光。此时,折射光线与反射光线成直角。
起偏振角遵从布儒斯特定律:当光线从$n_2$折射率介质入射到$n_1$折射率介质表面时,起偏振角满足 $\tan i_0=\cfrac {n_2} {n_1}$
计算要求:★布儒斯特定律应用
典型习题:三、4
四、双折射现象
1. 规律
光线射入双折射晶体后,在晶体内分为$o$光和$e$光,$o$光和$e$光都是线偏振光。
2. 方解石晶体的双折射
1)晶体的光轴: 晶体中存在一个特殊的方向,当光线沿这一方向传播时不发生双折射现象。
2)主截面: 入射表面的法线与光轴所构成的平面
3)(当入射光线平行于主截面时)$o$光的振动方向垂直于主截面;$e$光的振动方向平行于主截面。典型图示为:
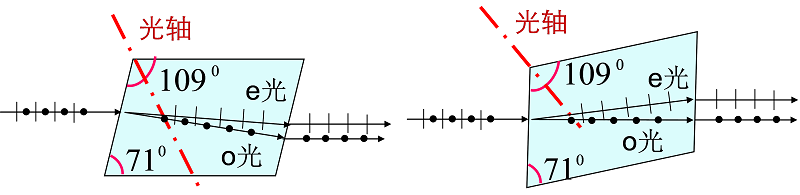
图中菱形为沿主截面的晶体剖面。
3. 双折射现象的定性解释
两种振动分量(垂直主截面的振动,$o$光,和平行主截面的振动,$e$光)的波阵面形状不同,$o$光波振面是球形,$e$光波阵面是椭球形。按惠更斯原理,画图可只,$o$光、$e$光传播方向的区别。
4. 双折射现象的特例
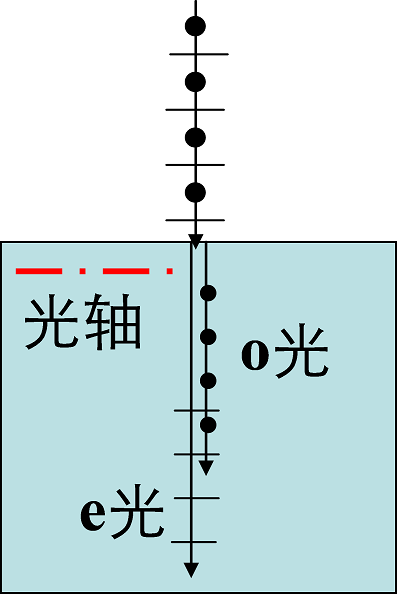
当光轴平行于表面,且入射光垂直入射时,发生了双折射现象,但$o$光、$e$光传播方向相同(仅传播速度不同,一快一慢)
5. 应用-尼科尔棱镜
尼科尔棱镜可当作是偏振片看待,其透振方向平行于主平面,如下图:
![]()
五、波片
波片是从双折射晶体中切割下来的平行平面薄片,其表面与晶体光轴方向平行。自然光垂直入射时,$o$光、$e$光传播方向相同,但传播速度不同。透过后,$o$光、$e$光之间将形成相位差。
$1/4$波片产生$(2k+1)\cfrac \pi 2$的相位差
最小厚度:$d=\cfrac \lambda {4(n_o-n_e)}$
$1/2$波片产生$(2k+1)\pi$ 的相位差
最小厚度:$d=\cfrac \lambda {2(n_o-n_e)}$
六、偏振光的干涉
线偏振光进入波片后,分解为$o$光,$e$光两垂直分量。出波片后,量垂直分量具有固定相位差。若在其后再放一个偏振片,则$o$,$e$两垂直分量分别会在透振方向上贡献分量,所贡献的两分量相差恒定,且同方向,会产生干涉。

