PeiLingX
物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》第23课。
本系列及本专栏其他文章，建议收藏目录：
0) 开篇语
从第17课到21课，我们筚路蓝缕，终于完成了氢原子薛定谔方程的求解过程，成功还原了玻尔的氢原子能级，又解释了玻尔模型所不能解释的更多现象，并且用量子力学的思维方式(而不是玻尔旧量子论的方式)理解了其中各个能级以及相应本征态的物理图像和对称性。
看起来，我们到此为止似乎就掌握了氢原子核外电子的全部能量信息。
然而令人遗憾的是，这个模型和真实的物理情形其实还有一些看起来很细微的差异。
也许有同学马上会猜测：这是不是因为真实的物理世界中有外场存在，这些外场造成了能量的扰动，导致了理想模型和真实物理世界之间的偏差。
的确，外场的存在会在理想库仑势的基础上加上一些能量扰动，使哈密顿算符发生变化，从而导致能级发生移动、或者简并能级发生分裂(这在可观测的物理现象上体现为：某条光谱线在原位置附近分裂为若干条新的谱线)。
但是，如果理想模型与现实之间的差异仅仅来自于外场，那么对我们而言，要做的事情无非也就是在理想氢原子模型的哈密顿算符里加上一些额外的势能项，然后通过稍微复杂一些的计算，来得到更精确、更符合实验结果的答案。
虽然这个过程会让我们习得量子力学中一些非常重要的近似计算方法，但整个物理模型和结果都会在意料之中，并不会让人感到耳目一新。
好在实际情况其实比我们想象的更有意思。
稍后我们会看到，即使排除了外场的影响，在理想的孤立体系中，实际能级还是会和薛定谔方程的计算结果有所差异，甚至也会出现反常的分裂，这种无法利用简单的氢原子模型以及外场解释的异常，才是更值得我们兴奋的地方。
这节课里，我们将先看看外场下的能谱会发生怎样的变化，然后和实际的能谱作比较，去看看来自氢原子(以及类氢原子)体系自身的、无法用外场的影响解释的细微偏差。
而在对这些细微偏差进行一些半定量的分析时，我们将发现，一段新的奇妙旅程正在前方等着我们。
1) 能级分裂
原子光谱在外场下发生分裂的现象其实早在1896年就发现了(这甚至比卢瑟福提出原子结构模型还早)，是由荷兰物理学家塞曼(P. Zeeman)发现的，因此也叫做塞曼效应(Zeeman Effect)。
这个效应说的是原子光谱在磁场中发生分裂的现象，最早的实验是用钠做的，塞曼发现，钠元素的某条谱线在磁场中会变宽，后来经过更精确的实验，发现是谱线分裂成了若干条。
对于这个效应最早的解释是塞曼的老师、一位同样来自荷兰、虽然算不上顶流、但又时不时地会在物理书上露个脸的著名物理学家洛仑兹(H. Lorentz )(后面我们还会去欣赏他的另外一个重要成果)，他从经典电磁学的角度出发，引入了空间量子化的假设，给出了最早的解释(这甚至比普朗克的能量子假说还早)。
最终师徒二人也因此双双喜提1902年的炸药奖。
现在，我们要从薛定谔方程的解出发，来看看如何导出塞曼效应中能级分裂的结果。
我们知道，经典图像中，电子的绕核旋转会产生环形电流，从而产生一个垂直于旋转平面的磁矩。虽然量子力学中不再有轨道的概念，但是电子的平均角动量仍然会产生相同的效果。
现在，假设我们将氢原子放在一个匀强磁场中，并且取磁场所在的方向为$ \small z $方向。
那么，此时氢原子在$ \small z $方向的磁矩$ \small \mu_z $会和磁场相互作用，产生一项额外的能量：
$\small E_{B}\simeq\small \mu_zB=\frac{e}{2m_ec}L_{z}B \quad{\scriptsize(式23.1)}$
其中，$ \small B $为磁感应强度大小，$ \small L_{z} $为角动量$ \small z $分量，另外几个量同学们都熟悉，就不一一介绍了。
(其实这个能量中还有一项与$ \small x,y $坐标有关，但是由于数量级过小，所以我们这里直接忽略[1])
现在，我们将磁场产生的能量加到氢原子核外电子的总能量中：
$\small \begin{align} H&=\small \frac{p^2}{2m_e}+V+\frac{eB}{2m_ec}L_{z}\ &:=H_0+\frac{eB}{2m_ec}L_{z} \end{align} \quad{\scriptsize(式23.2)}$
然后轻车熟路地将它们算符化，形成新的薛定谔方程：
$\small \begin{align} \hat H\left|\psi\right>&=\left(\hat H_0+\frac{eB}{2m_ec}\hat L_z\right)\left|\psi\right>\end{align} \quad{\scriptsize(式23.3)}$
我们知道，当没有磁场存在的时候，氢原子方程的本征函数解序列$ \small \psi_{nlm} $可以由三个量子数$ \small n,l,m $来描述，它们分别对应能量、轨道角动量、轨道角动量$ \small z $分量这三个物理量的本征值。
而我们在第19课和第20课中知道，之所以选这三个物理量，是因为它们都是相互对易的，因此可以独立求解、最后构成一组完整的本征态基底。
这个对易性质为我们求解新的方程提供了非常大的便利。因为我们看到，抛开系数不谈，新的方程其实只多出了一个$ \small \hat L_{z} $算符，而它是和哈密顿算符、角动量算符对易的，因此原来的(无外场情形的)方程的本征函数解$ \small \psi_{nlm} $也是这个新方程的本征函数(当然，前提是球坐标的$ \small z $方向和磁场方向一致)。
这样事情就变得简单了，我们直接把本征函数代入式23.3，就可以利用本征值关系得到：
$\small \begin{align} \hat H\left|\psi_{nlm}\right>&=\left(\hat H_0+\frac{eB}{2m_ec}\hat L_z\right)\left|\psi_{nlm}\right>\\ &=\left(E_n+\frac{eB}{2m_ec}m\hbar\right)\left|\psi_{nlm}\right> \end{align} \quad{\scriptsize(式23.4)}$
相应地，新的能量本征值就近似为：
$\small E_{nlm}=E_n+\frac{eB}{2m_ec}m\hbar \quad{\scriptsize(式23.5)}$
这里顺便说一句，对于以碱金属为典型代表的所谓类氢原子而言，我们也能得到类似的结果，它们和氢原子唯一的区别在于，由于内层电子的屏蔽作用，最终“传递”给最外层电子的势场(称作“屏蔽库仑势”)会更加复杂。
这样带来的结果是不同角量子数的能级简并被消除(我们在第21课曾经提到过，角量子数的简并只在纯库仑势中出现)，也就是说最终的能级和角量子数$ \small l $也有关，记作$ \small E_{nl} $，于是，它们在磁场中发生的能级分裂也相应地记为：
$\small E_{nlm}\simeq E_{nl}+\frac{ZeB}{2m_ec}m\hbar \quad{\scriptsize(式23.6)}$
我们看到，当加上磁场后，这个能级不再单纯是$ \small n,l $的函数，还与磁量子数$ \small m $有关(现在我们可以仔细品味一下为什么$ \small m $叫做“磁量子数”了)，这意味着原来的简并能级$ \small E_{nl} $中关于磁量子数的简并被解除，分裂成了$ \small 2l+1 $个不同的能级(别忘了 $\small m $的取值范围)。
比如塞曼效应最经典的分裂，就是钠原子光谱的所谓D线(这里的D仅仅是光谱线的命名顺序，没有其他特别含义)的分裂，这个$D$线对应的是从$ \small \left|\psi_{nlm}\right>=\left|\psi_{31m}\right>$ (称为3p态)到$ \small \left|\psi_{nlm}\right>=\left|\psi_{300}\right> $(称为3s态)之间的跃迁放出的光子。
当没有外磁场时，我们知道，由于能级的简并，跃迁放出的光子频率为$ \scriptsize \nu=\frac{E_{31}-E_{30}}{h} $，与磁量子数$ \small m $无关。但当外场存在时，原来简并的3p能级$ \small E_{31} $就分裂为三个：
$\small \begin{cases} E_{3,1,-1}&=E_{31}-\frac{eB\hbar}{2m_ec}\\ E_{3,1,0}&=E_{31}\\ E_{3,1,1}&=E_{31}+\frac{eB\hbar}{2m_ec}\ \end{cases} \quad{\scriptsize(式23.7)}$
另一方面，由于3s态对应的角量子数$ \small l=0 $，不存在磁量子数的简并，因此能级仍然是一个，这样一来，从3p到3s之间的跃迁放出的光子频率也就分成了三个，于是我们就能看到，处在磁场中的钠原子原来的D谱线在原来的位置附近分裂成了三条新的谱线，这也与实验相符合[2]。
而除了磁场以外，我们自然还会合理猜想：外加电场时原子光谱也会发生分裂。这样的分裂也在实验上被观测到，叫做斯塔克效应(Stark Effect)，由德国物理学家斯塔克(J. Stark)于1913年发现。
关于斯塔克效应的计算过程，我们这里不再详细介绍，同学们有兴趣可以自行了解一下，大部分量子力学教材都会讲[3]，不过看懂这个过程的前提是要先了解一种叫做微扰论的近似计算的思想、以及相应的计算流程(我们会在整个系列末尾的补遗部分再来介绍)。
读到这里，也许有同学会想起我们在上节课留下了一个小伏笔：当物理上真实地规定了某个特殊方向的时候$($比如我们刚才讨论的加上某个方向的外场$ )$，氢原子的球对称性就会消失。这节课我们会来体会这一点，但这些讨论将会作为附录放到本课最后，现在为了不打乱节奏，我们还是回来关注塞曼效应。
我们前面对能级分裂进行了看似天衣无缝的计算，但遗憾的是，这个计算结果并不能完全解释磁场中所有的能级分裂现象，特别是当磁场比较弱时，人们发现原子光谱的分裂数量和距离都和利用薛定谔方程算出的结果对不上，这种现象被称为反常塞曼效应。
此外，人们后来还发现，只要测量足够精确，即使没有外场存在，在氢原子和碱金属的光谱中，有的谱线(比如我们刚才提到的D线)也会在频率的理论值附近“天然地”分裂成两条。
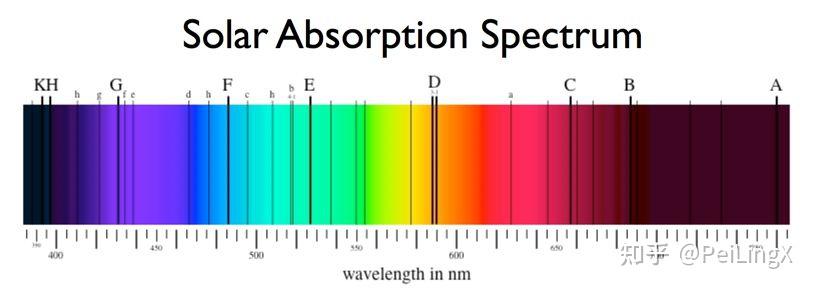
当时的物理学家们马上意识到，事出反常必有妖。
而名义上最早捉住这个“妖”的，又是两个荷兰物理学家，分别叫做乌伦贝克(G. Uhlenbeck)和古德斯密特(S. Goudsmit)，他们提出，这些现象背后包含着电子的一种全新的属性。
这个属性，就是在我们这个系列的第4课曾经露过一面、后来又久无音信的老朋友：自旋。
顺便说一句，其实早在乌伦贝克他们之前，一位名叫克罗尼西(R. Kronig，有的书上译作克罗尼克，这里按照德语发音习惯翻译 )的德国物理学家也曾经提出过自旋的概念，但他的观点很快招来了两位大佬：泡利和海森堡的反对，因为当时对电子自旋的理解是经典意义上的自转，而计算表明，这个“自转”将会使电子表面速度达到137倍光速，这违反了相对论。于是克罗尼西同学只好心灰意冷地收回了他的论文，却在几个月后眼睁睁看着乌伦贝克他们成为自旋的名义发现者。所以，有时候被大佬过分关照真的未必是件好事……
接下来，我们就来简单、定性地解释一下，如何利用自旋解释能级的“天然”分裂。
2) 旋-轨耦合
在第4课中我们看到，自旋从效果上可以类比为一个物体的“自转”，它产生的角动量和磁矩，与一个旋转的带电小球产生的效果在某些方面完全一样(以后我们会讨论不一样的地方)。
而另一方面，电子绕核运动的轨道角动量会产生环形电流的效果，从而产生磁场，这个磁场与自旋磁矩的相互作用，会形成新的耦合能，叫做旋$-$轨耦合(Spin-Orbit Coupling)。
它的抽象的算符形式是这样的[4]：
$\small \begin{align} \hat H_{LS}&=\frac{1}{2m_e^2c^2r}\frac{\text dV}{\text dr}\hat {\boldsymbol S}\cdot \hat {\boldsymbol L}\ \end{align} \quad{\scriptsize(式23.8)}$
(这一项又称为托马斯项(Thomas Term))
其中$ \small c $为真空中的光速，$\small \hat{\boldsymbol S} $为自旋角动量算符、$ \small \hat{\boldsymbol L} $为轨道角动量算符，而它们的内积$ \small \hat {\boldsymbol S}\cdot \hat {\boldsymbol L}$ (别忘了角动量是矢量)就非常直观地体现了旋( $\small \hat{\boldsymbol S} $)-轨( $\small \hat{\boldsymbol L} $)耦合。
(当然，严格来说，$ \small V $和$ \small r $都应该表示成算符形式)
而接下来我们会看到，能级的分裂，就来自于这项多出来的能量。
我们在第4、5课介绍自旋时，为了便于和实验结果联系起来，一直强调的是自旋产生的磁矩特性，但实际上，如果将自旋类比为自转，我们不难想象，自旋还具有角动量的特性。
只不过，与轨道角动量不同的是，它在某个给定方向上(比如 $\small z$ 方向)的自旋角动量本征值只有两个：$ \scriptsize \pm\frac{\hbar}{2}$ (这分别对应了向上的 $\small \left|z_+\right> $和向下的 $\small \left|z_-\right>$ 两个本征态)
而这一正一负两个本征值，正好会使旋$-$轨耦合对原来的能级产生一正一负两种扰动。
这两种扰动，就造成了原来简并的能级往高低两个方向分别产生移动，形成两个新的能级，而这两个新能级跃迁到其他能级上(特别是角量子数为0的能级上)，就会形成两条(或者其他偶数条)不同频率的分裂光谱线。
这样，我们就定性地解释了，为什么没有任何外场干扰的情况下，氢原子和碱金属原子也会观察到奇怪的双线(历史上是碱金属原子、而不是氢原子最先被观察到这个现象，同学们可以思考一下为什么[5])。
这里我们要注意：刚才在式23.8中，我们只是给出了旋$-$轨耦合能量的算符形式，还并没有具体算出它在各个简并能级上造成的能级分裂的具体幅度。这个计算我们将放到以后，等到介绍微扰论时再作为算例具体给出。
(如果我们熟悉了微扰论、并且找到了正确的能量本征态，这个计算其实并不难，到时候作者会帮同学们把计算思路梳理得明明白白，但现在还不是时候，一是因为准备不足，二是因为放在这里会占用太多篇幅，打乱我们轻快的步伐)
我们现在至少定性地明白了氢原子(以及类氢原子)光谱中反常的双线的来源，那么接下来的问题就是：这个两次出现在我们的旅程中的自旋，是个什么来头？
要知道这个答案，我们还需要再耐心地再等待几节课的时间，但在这节课里，我们至少可以先挖出一条重要线索，这条线索将带我们走进一处新的风景，并且最终找到一个更自然的引出自旋的方式。
3) 精细结构
实际上，当我们将能量的测量和计算的近似度提升到旋$-$轨耦合这个级别时，我们会发现，氢原子能谱其实还存在着其他两项相同数量级的偏差，它们虽然不会造成能级分裂，但会使能级发生偏移。
这两项偏差和旋$-$轨耦合的偏差合到一起，被统称为氢原子(以及类氢原子)的精细结构。
我们先来解释一下这两项偏差的来源。
先说第一项。
我们知道，薛定谔方程的哈密顿算符中，动能项源于牛顿力学模型(请回顾第8课中薛定谔方程的构造过程)：
$\small \hat T=\frac{\hat p^2}{2m_e} \quad{\scriptsize(式23.9)}$
而更精确的能量关系，本应该由相对论力学给出(我们下节课会具体说说这个式子的来源和更深层次的几何意义)：
$\small E^2=p^2c^2+m_e^2c^4 \quad{\scriptsize(式23.10)}$
(其中 $\small m_e$ 是电子的静质量)
相应地，动能应该是总能量减去静能量，即：
$\small T=\sqrt{p^2c^2+m_e^2c^4}-m_ec^2 \quad{\scriptsize(式23.11)}$
由于算符开根号实际上难于计算，因此我们可以将动能作为动量平方$ \small p^2 $的函数，然后在$ \small p^2=0 $附近泰勒展开：
$\small \begin{align} T(p^2)&=\left(m_ec^2+\frac{p^2}{2m_e}-\frac{p^4}{8m_e^3c^2}+\cdots\right)-m_ec^2\\ &=\frac{p^2}{2m_e}-\frac{p^4}{8m_e^3c^2}+\cdots \end{align} \quad{\scriptsize(式23.12)}$
忽略高阶项，新的动能与牛顿力学体系的动能就相差了一个$ \scriptsize -\frac{3p^4}{8m^3c^2} $，我们将它记为：
$\small H_{\text{Rel}}=-\frac{3p^4}{8m_e^3c^2} \quad{\scriptsize(式23.13)}$
这就是第一项偏差(当然，这只是算符层面的偏差，它在各能级上造成的能量本征值偏差还需具体计算，我们仍然放到将来介绍微扰论时再讨论)。
而第二项偏差，根据提出者的姓氏，被称为达尔文项(Darwin Term)。
(这个达尔文是写《物种起源》那个达尔文的孙子，祖传学术基因了属于是)
它的来源，可以简单看作真空中的能量涨落对电子的随机扰动，这种扰动使电子位置产生的不确定性[6]，这个不确定性的量级与电子的康普顿波长相当，这一项的具体形式和计算我们放到未来再说，现在我们暂时只需要知道它的存在就行了。
现在我们还是回头关注旋$-$轨耦合项，我们接下来要对它的量级做一个大致的评估，特别是要将它的量级和$ \small \hat H_{\text{Rel}} $的量级做一个对比，这将给我们带来一些新的线索。
4) 新的线索
相对比较严谨的量级估计，应该是先求出扰动项在各个能级本征态上的期望值表达式，然后进行估算。但现在，我们为了快速得到估算结果，不妨先参考张永德老师的书里的做法[7]，直接利用算符对应的经典力学量之间的物理关系，用半经典的方法来估算(我们这里会将估算思路写得更详细一些)。
(这里顺便多说一句，虽然我们已经有了更严谨的求解本征值问题的方法，但有时候适当利用经典物理图像去进行一些半定量的估计，还是非常有用的$($毕竟算符的期望值与经典力学量的测量值是一一对应的$ )$，至少它能帮助我们跳过求解本征值问题的繁琐计算，直接对结果进行一些合理猜测)
我们的主要做法是：
先利用经典力学的关系，将能量偏差中各个力学量表示成更基础的力学量(比如位置和动量)；
然后将它们化简成氢原子的库仑势(这代表了未经修正的氢原子能量)乘以一个系数的形式，这个系数就代表了能量偏差的量级。
具体到旋轨耦合项中，我们需要重点关注的自然就是两个角动量：$ \small \boldsymbol S $和$ \small \boldsymbol L$
根据我们在第$18$课中的讨论(或者经典力学的常识)，轨道角动量$ \small \boldsymbol L $可以表示为：
$\small\boldsymbol L={\boldsymbol x}\times {\boldsymbol p} \quad{\scriptsize(式23.14)}$
如果我们回到经典图像，假想电子绕核做圆周运动，那么轨道角动量的大小相当于圆周运动的半径和动量的乘积：
$\small L=rp \quad{\scriptsize(式23.15)}$
我们接下来看看自旋。
虽然自旋是一个纯粹的量子现象，没有经典的物理图像，也不可能和位置、动量这些经典力学量产生什么物理关系，但估算一下它与$ \small r,p $的量级关系仍然是可能的。
这需要我们暂时回到量子世界中，先比较一下自旋角动量和轨道角动量的本征值的量级。
首先，我们知道，自旋角动量的本征值为$ \scriptsize \pm\frac{\hbar}{2} $，现在我们将它与角量子数的本征值量级而某个坐标方向上的轨道角动量本征值为$ \small m\hbar $，由于磁量子数$ \small m $存在上下限$( \small \pm l )$，因此它是一个有限的整数。于是，两个本征值$ \scriptsize \pm\frac{\hbar}{2} $和$ \small m\hbar $仅仅相差一些有限的倍数，在量级上可以认为是一致的。
另一方面，根据本征值和经典力学测量值之间的关系，我们可以大胆地相信：本征值在量级上的一致性，也可以对应到经典力学量本身在量级上的一致性。
于是，和轨道角动量类似，我们也可以估算出自旋角动量在量级上也满足类似关系：
$\small S\sim rp \quad{\scriptsize(式23.16)}$
(注意，这里的波浪线符号 $\small \sim$ 仅仅表示两者在量级上相当，并不代表两者相等，更不代表它们之间有任何真实的物理关系)
接下来，我们将两个角动量与位置和动量的量级关系代入旋-轨耦合项(式23.8)中，可以得到：
$\small H_{LS}\sim \frac{1}{2m_e^2c^2r}\frac{\text dV}{\text dr}r^2p^2 \quad{\scriptsize(式23.17)}$
而在氢原子的库仑势中，$ \scriptsize \frac{\text dV}{\text dr}=\frac{e^2}{r^2}$ (这里我们忽略了 $\scriptsize \frac{1}{4\pi\epsilon_0}$ 因子以图清净，后面也做相同处理)，于是上式可以进一步化为：
$\small \begin{align} H_{LS}&\sim \frac{1}{2m_e^2c^2r}\frac{e^2}{r^2}r^2p^2\\ &\sim \frac{1}{2}\frac{e^2}{r}\frac{p^2}{m_e^2c^2}\\ &\sim V_{\text{C}}\frac{p^2}{m_e^2c^2} \end{align} \quad{\scriptsize(式23.18)}$
其中$ \small V_{\text C} $代表库仑势。
而如果我们还没有在量子世界中修炼得走火入魔，那么我们一定还记得动量的远古定义：$ \small p=mv$ (而不是我们现在更熟悉的 $\small \hat p=-\text i\hbar\boldsymbol\nabla$ )，将它代入式23.18，我们将会得到：
$\small \begin{align} E_{LS}&\sim V_{\text{C}}\frac{v^2}{c^2} \end{align} \quad{\scriptsize(式23.19)}$
接下来，我们将上面的量级与前面提到的动能偏差项$ \small H_{\text{Rel}} $做个对比。
我们先将$ \small H_{\text{Rel}} $的式23.13也做一些(中学生也会的)变形：
$\small \begin{align} H_{\text{Rel}}&=\frac{3p^4}{8m_e^3c^2}\\ &=\frac{3p^2}{8m_e}\frac{p^2}{m_e^2c^2}\\ &=\left(\frac{3}{8}m_ev^2\right)\frac{v^2}{c^2} \end{align} \quad{\scriptsize(式23.20)}$
而利用经典力学里库仑场中的圆周运动向心力关系：
$\small \begin{align} \frac{m_ev^2}{r}=\frac{e^2}{r^2} \end{align} \quad{\scriptsize(式23.21)}$
可得：
$\small \begin{align} m_ev^2=\frac{e^2}{r}= V_{\text{C}} \end{align} \quad{\scriptsize(式23.22)}$
于是：
$\small \begin{align} H_{\text{Rel}}&\sim V_{\text C}\frac{v^2}{c^2} \end{align} \quad{\scriptsize(式23.23)}$
这样，我们发现，旋$-$轨耦合产生的能量偏差$ \small H_{LS} $和动能的相对论偏差$ \small H_{\text{Rel}} $在数量级上是一样的(虽然我们目前仅仅是从经典图景中得到这个结论)，都是在初始的库仑势(以及相同量级的动能)的基础上加上了$ \scriptsize \frac{v^2}{c^2} $这个相对大小的修正。
而且，如果同学们对相对论基础还有印象，一定会记得，$ \scriptsize \frac{v^2}{c^2} $这个因子在相对论中随处可见(比如钟慢、尺缩、以及前面给出的能量关系，我们下节课会再次提到)。
这不得不让人浮想联翩：难道自旋和相对论之间也有着扯不清道不明的关系？
的确是这样，而且，除了旋轨耦合$ \small H_{LS} $以及本身就来自于相对论偏差的$ \small H_{\text{Rel}} $，那个由真空中的量子涨落产生的达尔文项也和相对论有关(我们这里仍然不详细讨论，有兴趣的同学还是推荐看张永德老师的书[8])。
所以，走到这里，我们其实已经不知不觉地来到了一个会合点：狭义相对论和量子力学的会合点。
接下来的路，将是一段新的奇妙旅程，我们将看看，当量子力学遇上狭义相对论时，会孕育出什么奇花异草(会开出一朵名叫“自旋”的奇花吗？)
下节课，我们就先来简单聊聊，相对论的中心思想都讲了些啥。
不过，结束本课之前，我们还要续上前面留下的一个小尾巴：简单说一说，外场如何破坏氢原子模型的球对称性。
附：对称性的消失
我们在上节课提到过，理想的氢原子方程解是具有球对称性的，虽然作为本征函数的球谐函数自身并不具有几何上的球对称性，但这仅仅是因为数学上规定了$ \small z $轴的取向，在在物理上，任何一个方向都可以成为$ \small z $轴，因此本征函数的方向其实是任意的。
但是，当我们真正通过物理方式(比如施加特定方向的磁场)给出了一个特殊的$ \small z $方向的时候，这种简并就被解除了，而球对称性也会随之消失(毕竟外场本身是不具有球对称性的)。
现在我们先来证明这一点。
在第20、21课中我们知道，数学上指定了$ \small z $轴、建立了球坐标之后，我们就能在这个球坐标的表象下求解薛定谔方程，得到一组本征态解$ \small \left|\psi_{nlm}\right>$
而在第22课关于球对称性的讨论中我们知道，如果对这些本征态进行空间旋转，那么旋转后得到的新的态仍然是同一简并能级$ \small E_{nl} $的本征态(这里写出角量子数 $\small l$ 是因为这些本征态的角量子数也相同)。
而由于旋转变换是线性的，因此我们不妨将旋转后的某个新的态矢量$ \small \left|\psi'\right> $表示为旋转前的本征态组$ \small \left|\psi_{nlm}\right> $的线性组合：
$\small \left|\psi'\right>=\sum_{k}c_k\left|\psi_{nlm_k}\right> \quad{\scriptsize(式23.24)}$
$( \small m_k$ 代表不同的磁量子数)
为了方便计算，我们不妨假设旋转后的态矢量为：
$\small \left|\psi'\right>=c_1\left|\psi_{nlm_1}\right>+c_2\left|\psi_{nlm_2}\right> \quad{\scriptsize(式23.25)}$
(虽然实际上简并态的个数是 $\small 2l+1$ ，但我们不妨只选取其中两个)
那么，哈密顿算符作用在上面，形式上就是：
$\small \hat H\left|\psi'\right>=c_1\hat H\left|\psi_{nlm_1}\right>+c_2\hat H\left|\psi_{nlm_2}\right> \quad{\scriptsize(式23.26)}$
当没有外场存在时，$ \small \left|\psi_{nlm_1}\right>,\left|\psi_{nlm_2}\right> $都是同一能级的能量本征态，于是：
$\small \begin{align} \hat H\left|\psi'\right>&=c_1\hat H\left|\psi_{nlm_1}\right>+c_2\hat H\left|\psi_{nlm_2}\right>\\ &=c_1E_{nl}\left|\psi_{nlm_1}\right>+c_2E_{nl}\left|\psi_{nlm_2}\right>\\ &=E_{nl}\left(c_1\left|\psi_{nlm_1}\right>+c_2\left|\psi_{nlm_2}\right>\right)\\ &=E_{nl}\left|\psi'\right> \end{align} \quad{\scriptsize(式23.27)}$
因此$ \small \left|\psi'\right> $仍然是$ \small \hat H $的本征态，本征态的取向具有任意的方向性、或者说球对称性。
但当我们加上了外场(比如说磁场)时，通过前面对塞曼效应计算给出结果(式23.7)可知，不同的磁量子数将对应不同的能级，此时：
$\small \begin{align} \hat H\left|\psi'\right>&=c_1\hat H'\left|\psi_{nlm_1}\right>+c_2\hat H'\left|\psi_{nlm_2}\right>\\ &=c_1E_{nlm_1}\left|\psi_{nlm_1}\right>+c_2E_{nlm_2}\left|\psi_{nlm_2}\right> \end{align} \quad{\scriptsize(式23.28)}$
除非$ \small c_1=0 $或$ \small c_2=0$ ，否则等式右边不再能合并成$ \small E_{nl}\left|\psi\right> $的形式，这说明能量本征态的取向具有了特殊的方向性，也就是球对称性从物理上被破坏了。
参考
- 关于被忽略的这一项，可参考：《量子力学(第二版)》，苏汝铿 著，P. 258
- 其实这里讨论的是能级分裂比较简单的一种情况，它的妙处在于$ \small 3lm$能级分裂的个数与观察到的谱线分裂条数正好一致，都是3条；而对于角量子数$ \small l$更大的一些其他能级分裂而言，最终观察到的谱线分裂条数与$\small 2l+1$并不一一对应，对这个现象有兴趣的同学可以翻阅《量子物理学(上册)》捷列文斯基 著，丁亦兵等 译，P.573~p.574
- 个人觉得讲得最清楚的是顾樵《量子力学 Ⅱ》P. 418~P. 421
- 推导过程可参考张永德《量子力学(第四版)》P. 193~P. 194
- 或者参考曾谨言《量子力学 卷Ⅰ(第四版)》P. 299
- 如果想对此有一个比较直观的物理图像，可参考《量子物理学(上册)》捷列文斯基 著，丁亦兵等译，P. 546~P. 547
- 张永德《量子力学(第四版)》， P .193 ~ P. 194, P. 204 ~ P. 205
- 张永德《量子力学(第四版)》， P. 204 ~ P. 205
编辑于 2022-10-25 12:17