PeiLingX
物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》的第15课，本课是对前半程(也就是我们这个系列的基础篇)的回顾和脉络梳理。
了解本系列及本专栏其他文章，请收藏目录：
1) 回顾
在本系列的第1课里，我们开宗明义地提到：
量子力学中，描述一个物理对象所处状态的基本方式，不再是位置速度动量能量等经典力学量，而是态空间中抽象的态矢量，也就是我们通常所说的“量子态”。
- 态矢量
一个态矢量，按狄拉克符号记法，分为左矢⟨ψ|和右矢|ψ⟩，可以类比为线性代数中互为共轭转置的一对行向量和列向量：
u†=(u∗1,u∗2,⋯,u∗n), u=[u1u2⋮un]
通常情况下，我们用右矢表示一个态矢量。
为了理解态矢量，我们最初以“薛定谔的猫”思想实验为引子，用态矢量解释了“既生又死”的“叠加态”：将“活猫”和“死猫”两种确定状态看作一组基底，于是既生又死的叠加态就是这组基底的线性叠加：
|ψ⟩=a1|L⟩+a2|D⟩
两个系数的模方|a1|2,|a2|2分别代表打开盒子观察猫的状态时，观察到活猫和死猫的概率。
于是根据概率归一化条件，可知a1,a2满足：
|a1|2+|a2|2=1
而我们又提到，如果将“猫的死活”看成一个虚构的力学量，那么“死猫”和“活猫”两种确定状态就是这个力学量的本征态。
- 本征态
当我们对物理对象测量某个力学量F时，物理对象将随机坍缩到某些由F决定的特定状态上，这些态就是F的本征态，记为|Fn⟩。
比如我们在第4课和第5课中提到的电子在z方向的自旋，就有两个本征态|z+⟩和|z−⟩，也就是说，当我们用Stern-Gerlach实验装置测量电子在z方向的自旋时，只会随机得到|z+⟩和|z−⟩两个方向，而不会出现其他方向的结果。
又比如我们在第8课提到的定态薛定谔方程的解，就是能量的本征态。
一个物理对象的态矢量通常并不处于某个力学量的本征态上，而是本征态的线性叠加，这就是所谓的叠加态(就像黑盒子里的猫没被观察之前那个“既生又死”的状态一样)。
- 叠加态
一个一般的态矢量，可以表示成某个力学量ˆF的本征态的线性组合：
|ψ⟩=∑ncn|Fn⟩
就像线性代数中一个向量可以表示成一组由矩阵特征向量构成的基底的线性叠加：
u=∑nk=1ukαk
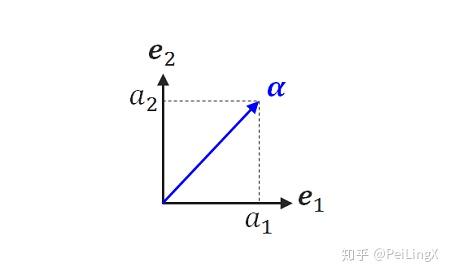
但是量子力学中的分量系数还有一层重要的物理意义：测量结果的概率。
- 量子力学中的测量
对处于一个一般状态状态|ψ⟩=∑ncn|Fn⟩的物理对象，如果去测量它的力学量F，那么它的状态将随机坍缩到其中一个本征态|Fn⟩，相应的概率是cn的模方|cn|2
而到此为止，我们一直都在讨论抽象的量子态，而还没有说到经典力学量的测量值在量子力学中如何出现。而这就要提到本征值。
- 本征值
量子力学中，对物理对象测量某个物理量F时，可能出现的值，就是该力学量的本征值。
而本征值和本征态是一一对应的。
当一个粒子的态矢量处于物理量F的某个本征态|Fn⟩时，它就具有确定的F值，此时对它测量物理量F，就会百分之百得到相应的本征值，记为Fn
需要提一句的是，到此为止自，我们一直用n作为下标，似乎意味着本征值总是离散的，但实际上本征值也可能是连续的，比如下面这个例子：
一维情形下一个粒子的位置坐标x (这是我们能想到的最简单的力学量)
我们将粒子位置的某个本征态记为|xa⟩,xa∈R
我们假设某个粒子处于状态：
|ψ⟩=∑xaψ(xa)|xa⟩
(由于x∈R，所以这里的求和其实是对x积分，只是我们现在没给出它的具体形式)
对于这个粒子，如果我们去测量它的位置坐标，那么它的状态将随机坍缩到某个本征态|xa⟩，而作为测量的结果，我们会测得粒子的位置x=xa，这就是本征态|xa⟩对应的本征值，而我们得到这个结果的概率密度为|ψ(xa)|2
而由于本征值和本征态可以分别类比为线性代数中矩阵的特征值和特征向量，因此，量子力学中，一个力学量也会对应一种类似矩阵的东西，这叫做力学量算符。
- 算符
力学量算符：一个经典力学量F在量子力学中变成算符ˆF，它可以类比为线性代数中的矩阵，而相应的本征值和本征态序列Fn和|Fn⟩就可以类比为矩阵的特征值和特征向量。
而在线性代数中我们知道，一个矩阵A与它的特征值λn、特征向量αn之间满足：
Aαn=λnαn
作为类比，我们可以形式上写出算符的本征值关系：
ˆF|Fa⟩=fa|Fa⟩
为了便于直观理解，我们可以将这个式子做一个不严谨的解释：
当一个粒子处于力学量F的某个本征态|Fn⟩时，对它测量F本身(等式左边)，会百分之百得到本征值fn的结果，并且测量后粒子仍然处于本征态|Fn⟩ (等式右边)
对于可观测的力学量而言，它的本征值是实数，在量子力学中对应的算符称作厄米算符，不过我们现在还不用去了解厄米算符的具体定义。
另外，当我们关注的力学量是能量时，它的本征值关系会变成定态薛定谔方程。为了实现这一点，我们需要先将抽象的算符和态矢量“具象化”，这就要提到表象了。
- 表象
在线性代数中我们知道，向量和矩阵的具体形式需要在具体的基底下写出。
以向量为例，同一个向量a在不同基底下会有不同的投影分量：
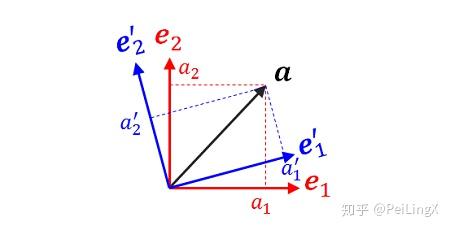
这些分量的值就构成了向量a在不同基底下的具体形式：
(a1,a2,⋯,an)T或(a′1,a′2,⋯,a′n)T
类似地，态矢量和算符也需要在具体的“表象”下写出，不同的表象下，态矢量和算符都会有不同的分量形式，而我们要讨论的最常见的表象是“坐标表象”。
- 坐标表象
当我们使用坐标表象来表示一个物理对象的态矢量时，就等于选取了坐标的本征态|xa⟩作为基底，根据态矢量的线性叠加关系，我们知道：
|ψ⟩=∑xaψ(xa)|xa⟩
类比向量的分量形式，我们不难知道，这里与坐标xa有关的系数ψ(xa)其实就是态矢量|ψ⟩在坐标表象下的具体形式，它也满足内积关系：
ψ(xa)=⟨xa|ψ⟩=∫Rδ(x−xa)ψ(x)dx
其中δ(x−xa)就是坐标的本征态|xa⟩在自身的表象、也就是坐标表象下的具体函数形式，类似于一组正交归一的向量{ek}在自身为基底的坐标系中的分量为：
ek=(0,0,⋯,1(第k个分量),0,⋯,0)T
对式15,x取遍所有的xa，我们就还原了函数ψ(x)，而如果再考虑到它会随着时间发生演化，我们还能将它写成ψ(x,t)，这就是我们熟悉的波函数。
除了态矢量以外，各种力学量的算符在坐标表象下也有具体的形式，比如我们接下来要讨论的能量算符、也就是哈密顿算符ˆH
- 哈密顿算符
在牛顿力学中，一个运动物体的能量由动能和势能组成：
E=Ek+Ep=p22m+V
其中p是物体的动量，V是物体所处位置的势能。
而在量子力学中，能量、动量、势能也有相应的算符，这些算符也满足相同的关系，即：
ˆH=ˆp22m+ˆV
而动量算符和势能算符在坐标表象下具有简单的形式，分别为：
ˆp=iℏ∂∂x,ˆV=V(x)
(我们在第9课中看到，这可以在自由粒子的单色波函数中，通过德布罗意关系得到验证)
于是哈密顿算符在坐标表象下可以写成：
ˆH=−ℏ22m∂2∂x2+V(x)
此时我们离量子力学中最重要的定态薛定谔方程就只有一步之遥了。
- 定态薛定谔方程
能量本征值关系：
ˆH|a⟩=Ea|a⟩
哈密顿算符在坐标表象下为：
ˆH=−ℏ22m∂2∂x2+V(x)
能量本征态|a⟩作为态矢量，可以表示成一般的波函数形式ψa(x)(不考虑时间变化的部分)，这样，我们就得到了一个微分方程：
−ℏ22m∂2∂x2ψ+Vψ=Eψ
这就是定态薛定谔方程。
由于它是能量本征方程在坐标表象下的具体形式，因此我们可以很自然地想到，它的一系列解ψa(x)就是能量本征态在坐标表象下的具体形式(在原子核外电子的薛定谔方程中，这就是代表电子在空间中概率分布的电子云)，而等式右边相应的常数Ea就是能量本征值。
特别地，在束缚态或周期势中，我们会得到离散的解ψn(x)以及离散的能量本征值En，这也是分立能级的来源(我们在第10课中对此进行了定性的解释)。
另外，我们知道，不同的势能会对应不同的哈密顿算符，也就会对应不同的能量本征值和本征态，这个常识将是我们在未来的课程中继续理解能级跃迁和能级分裂的基础。
但定态薛定谔方程只能看做薛定谔方程的空间部分，当我们关注量子态随时间的演化时，我们就会得到完整的薛定谔方程。
- 态的时间演化与薛定谔方程
我们直接给出了态的时间演化规律与哈密顿算符的关系：
∂∂t|ψ⟩=ˆHiℏ|ψ⟩
也就是说，量子态的演化可以看作哈密顿量作用在态矢量上的结果。
如果我们将iℏ移到左边，然后将前面给出的坐标表象下哈密顿算符的具体形式，就得到一个新方程：
iℏ∂∂tψ(x,t)=(−ℏ22m∂2∂x2+V)ψ(x,t)
这就是薛定谔方程。
到此为止，我们就梳理完了从态矢量到波函数、再到薛定谔方程、最后到分立能级这条主线。
接下来，我们来梳理基础篇中的另一条主线：不确定性原理。
- 本征态“相互投影”与不确定性
在第3课的假想实验中，我们看到，两个不同力学量的本征态有可能是“不重合”的，也就是说，一个力学量A的本征态可能会在另一个力学量B的本征态上产生“投影”。
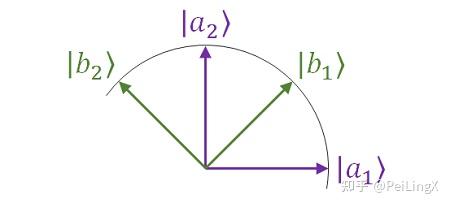
这种情况下，当物理对象处于力学量A的本征态、即具有确定的A值时，如果对它测量力学量B，就不会得到一个确定的本征值，而是会随机落到B的某个本征态|bk⟩上，同时随机得到一个本征值bk
从测量结果的角度来看，就是当力学量A具有确定值时，力学量B就变得不确定了。
这就是我们对不确定性原理的最粗浅的理解。
而这样的一对力学量的关系被称为是“不对易”的，这可以类比于线性代数中两个矩阵的不可交换性，即：
AB−BA≠0
而在第4课和第5课介绍的斯特恩−盖拉赫实验(后文简称SG实验)中我们看到了一个物理实例：电子在不同方向的自旋是无法同时确定、也就是不对易的。
而量子力学中最基础的一对不对易的力学量是坐标和同方向上的动量，比如x坐标以及x方向的动量px
(我们在第14课中顺便提及过，它们之间的对易关系为：
[ˆx,ˆp]:=ˆxˆp−ˆpˆx=iℏ
我们在基础篇中并未太多用到这个关系，但进阶篇中我们会看到它的作用)
它们之间有一个著名的不确定性关系：
ΔxΔpx≥ℏ2
我们用了三节课内容讨论这个关系背后的线性代数本质和证明过程，其中用到了一个关键信息，就是坐标和动量之间的表象变换。
- 表象变换与不确定性关系的证明
由于坐标和动量的本征态都是在无穷维的函数空间中，不像有限维空间中基底之间的关系那么直观。
因此，我们专门用了一节课内容来导出它们的表象变换关系。
最后我们惊喜地发现这竟然就是傅里叶变换：
ψ(x)=1√2πℏ∫ϕ(p)eiℏpxdp
在此基础上，我们在第13课中借用泛函分析中柯西-施瓦茨不等式的一个推论，给出了不确定性关系的证明。
- 量子与经典的连结
而作为基础篇的结尾，我们通过考察动量的期望值的时间变化，从薛定谔方程出发导出了牛顿第二定律，完成了一次量子世界与经典世界之间的连结。
现在，让我们回顾一下第1课开篇提到的那些初学者的疑惑，看看我们有了哪些新的理解。
2) 第1课的疑惑与解答
Q1：我们知道，原子核外的电子具有看起来不合常理的分立能级，也就是只能取一些不连续的特殊值。那么这些特殊值是怎么来的呢？
A1：能级与能态 = 薛定谔方程的基础解系=能量的本征值和本征态，分立能级对应着束缚态下分立的能量本征值。
Q2：电子在不同能级之间会“跳来跳去”进行跃迁，同时吸收或发射光子，这个跃迁是怎么发生的呢？
A2：这个和哈密顿算符的含时变化有关，我们还没有解释，但我们会在进阶篇中讨论。
Q3：又比如，我们知道微观粒子具有波粒二象性，物理课本告诉我们，微观粒子既是粒子又是波，但我们其实只是记住了这句话，这种奇怪的二重性质有没有更好的理解方式呢？
A3：我们在第12课中通过态矢量的动量表象和坐标表象理解了这样的双重性质。
Q4：而我们又知道，描述粒子波动性的是波函数，并且隐约知道所谓哥本哈根诠释：波函数可以用来计算粒子在某个位置出现的概率。那么这个奇怪的概率波要怎么和我们熟悉的经典物理量联系起来呢？
A4：波函数 = 态矢量在坐标表象下的具体函数形式，类似于向量在某一组基底下的具体分量形式，粒子在某个位置出现的概率就是它在该位置对应的坐标本征态上的“投影长度”的模平方。
Q5：而决定波函数行为的是一个叫作薛定谔方程的微分方程，我们知道它在量子力学中的地位如同牛顿第二定律在经典力学中的地位，那么薛定谔方程的物理意义是什么？它和经典力学定律之间是不是也能联系起来呢？
A5-a：定态薛定谔方程 = 能量的本征值关系在坐标表象下展现出的一个具体微分方程形式；
A5-b：薛定谔方程 = 量子态的时间演化规律在坐标表象下展现出的一个具体微分方程形式；
A5-c：薛定谔方程与牛顿第二定律之间可以通过本征值的期望值的时间演化来联系。
Q6：另外，我们听说过海森堡不确定性原理，它告诉我们，有些物理量会像一对冤家一样不能同时具有确定值，比如位置和动量，一个确定了，另一个就变得随机。那么，造成两者不能同时确定的更深层次原因是什么呢？
A6：不确定性 = 两个算符不对易，或者它们的本征态“不重合”，相互之间有“投影”。当一个力学量A处于确定的本征态时，“投影到”另一个与它不对易的力学量B的本征态组，就会产生多个非零的“投影分量”，也就是说B可能出现多个不同的测量结果，这就对应着B的不确定了。
Q7：最后，最让我们困惑的是，这一大堆现象和结论看起来完全是散装在一起的，表面上看不出任何联系，它们真的是来自同一个量子力学理论体系吗？
A7：我们看到，通过态矢量的叠加原理、算符-本征值-本征态的关系，我们将前面提到的现象都串了起来。
至此，除了第2个问题没有得到详细解释外，我们的疑惑基本上就都得到了解答。
3) 总结与预告
在基础篇里，我们借用与线性代数的类比，从零开始建立了量子力学最基础的理论框架，也解释了一些初学者常见的疑惑。
但是，我们的基础篇还是留了一些遗憾：
我们更侧重理论框架和数学上的类比，物理味道反而并不那么浓厚；
另外，我们在基础篇里讨论到的模型，其实都是比较简单的一维模型，一维世界的好处是从数学上容易理解，但它却少了很多真实三维世界的乐趣(比如对称性)；
最后，我们直到现在讨论的量子力学，都是在都是牛顿力学的微观版本(因为我们的哈密顿算符是用经典能量关系 ˆH=ˆp22m+ˆV 表示的)，我们还没看到，如果在相对论的时空关系中建立量子力学，会出现什么样意想不到的结果。
在接下来的进阶篇里，我们就要进入更真实的物理世界，在其中感受数学形式与物理图景的完美结合：
编辑于 2021-12-14 16:15