物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》的第10课。
了解本系列其他文章,请收藏目录:
0) 开篇语
在第1课的开篇语中,我们曾经提到过,要从量子力学的数学本质的角度,来理解粒子在束缚条件下为什么会存在分立能级(这也正是“量子”一词的最初来源 )。
而在第6课中,我们又提到,分立能级的本质,就是(势场束缚下 )哈密顿算符对应的能量本征值,类比到线性代数中矩阵的特征值只能取到一些离散值而不是整个实数域,我们就能从一个抽象的角度理解分立能级的存在。
但这毕竟还只是一种类比的理解,而不是真正的推导和计算。本课里,我们将通过一个简单的例子,求解一遍薛定谔方程,算出这种分立的能级来。
准确地说,我们需要求解的,其实是薛定谔方程的“空间部分”,也就是我们在第8课见到的定态薛定谔方程:
$\small \left[-\frac{\hbar^2}{2m}\nabla^2+V(x,y,z)\right]\psi=E\psi \quad\scriptsize{(式8.18)}$
因为它本质上就是能量的本征方程,所以从它出发得到能量的本征值以及本征态,是理所当然的事情。
(学过数学物理方程的同学不难想到,这个方程可以通过对薛定谔方程分离变量求解,不过不知道什么是分离变量法也没关系,我们以后会解释,它和常微分方程的分离变量法稍微有些不一样,但也还是比较容易理解的 )
这一课,我们就来体验一下这个求解过程。
1) 哈密顿算符与势能
首先,我们要再温习一下第9课中提到的一个常识:哈密顿算符是随着势能的变化的。
在第8课中,我们提到,定态薛定谔方程(式8.18 )左边括号中第一项是动能算符 $\small \hat{T}=\frac{\hat{p}^2}{2m}$ 在坐标表象下的具体形式,第二项是势能算符 $\small \hat{V}$ 在坐标表象下的具体形式。
我们在第9课中又顺便提到过,这两项中,动能项的函数形式是固定不变的(永远是 $\small \frac{\hat p^2}{2m} $),而第二项的函数式却会随着势能条件而改变,从而给出不同的哈密顿算符,最终也会得到不同的能量本征值和本征态序列(以波函数形式呈现,又叫本征函数 )。
比如,在氢原子的薛定谔方程中、势能函数为库仑势:
$\small V(x,y,z)=-\frac{1}{4\pi\varepsilon_0}\frac{e^2}{\sqrt{x^2+y^2+z^2}} \quad\scriptsize{(式10.1)}$
这个势能通常被写成球对称的形式:
$\small V(r)=-\frac{1}{4\pi\varepsilon_0}\frac{e^2}{r} \quad\scriptsize{(式10.2)}$
在这个势能条件下,我们将通过一段复杂的计算,得到一系列能量本质值和本征函数解(同时认识一大堆特殊函数 ),这些本征值看起来完全符合玻尔氢原子模型:
$\small E_n=-\frac{1}{n^2}\frac{m_e e^4}{8h^2\varepsilon_0^2} \quad {\scriptsize(式10.3)}$
但以后我们会知道,它们对应的本征函数还包含着波尔理论无法触及的更精妙的结构,不过这些内容需要单独展开介绍,我们将它放到本系列的进阶篇里(第16课以后 )去体会。
为了用更快的方式达到我们这节课的目的(感受求解薛定谔方程和分立能级来源的过程 ),我们将找一个最简单的势能模型(比真空中的球形鸡还简单 ),着手寻找分立能级,这个模型叫作“一维无限深势阱”。
它的好处在于,简单易懂的同时又能保持风味不减,在它的求解过程中,我们仍然能完整体会到求解薛定谔方程寻找分立能级的乐趣。
(也正因为如此,大部分量子力学教材都把它作为求解薛定谔方程的第一个案例 )
而且,还有一点很重要的是,它的本征函数形式也非常简单,简单到我们一眼就能认出来。
2) 一维无限深势阱
这个物理模型是这样的:
一个粒子被囚禁在一个宽度为 $\small L$ 的、两端“封闭”的一维势场内,这个势场内部势能为0,外部势能为无穷大,这样的情形下,粒子将没有任何可能从势场两端逃逸出。
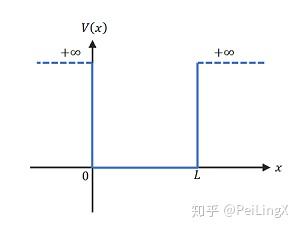
为了有个物理直观,我们可以想象一段有限长导线内的一个电子,它在导线内可以自由移动,但到了导线边缘,就会被来自导线内部的强大库仑势束缚住,几乎无法逃逸出去。
我们将其中一端的坐标设为0,另一端坐标设为 $\small L$,那么势能函数为:
$\small V(x)=\begin{cases} 0 & x\in\left(0,L\right)\\ +\infty & \text{otherwise} \end{cases} \quad\scriptsize{(式10.4)}$
于是在粒子所在的势阱内,势能项变成0,方程简化为没有势能项的形式:
$\small -\frac{\hbar^2}{2m}\frac{\text d^2}{\text d x^2}\psi=E\psi \quad\scriptsize{(式10.5)}$
对于这样一个二阶线性微分方程,我们可以很快知道,它的解具有这样的形式:
$\small \psi(x)=A\sin{(kx)}+B\cos{(kx)} \quad\scriptsize{(式10.6)}$
其中 $\small k=\frac{\sqrt{2mE}}{\hbar}$ ,可以看出,它就是这个波的波数。
而根据这个物理情形的假设,粒子出现在势阱区域外的概率为0,结合波函数的概率诠释,这就意味着:
$\small |\psi(x)|^2\equiv 0\quad (x\notin(0,L)) \quad\scriptsize{(式10.8)}$
也就意味着:
$\small \psi(x)\equiv 0\quad (x\notin(0,L)) \quad\scriptsize{(式10.9)}$
而波函数在势阱内连续,不可能在边界发生突变,所以势阱两端边界上的波函数也一定为0,这样我们可以得到这个方程的两个边界条件:
$\small \psi(0)=0, \ \psi(L)=0 \quad\scriptsize{(式10.10)}$
根据第一个边界条件,我们可以得出 $\small B=0$ ,这样,波函数简化为:
$\small \psi(x)=A\sin{(kx)} \quad\scriptsize{(式10.11)}$
再根据第二个边界条件,我们有:
$\small A\sin{\left(kL\right)}=0 \quad\scriptsize{(式10.12)}$
这意味着 $\small A=0$ 或 $\small \sin{\left(kL\right)}=0$ ,而前者将导致整个波函数为0,变为平凡解,不符合物理事实,所以我们取:
$\small \sin{\left(kL\right)}=0 \quad\scriptsize{(式10.13)}$
这就意味着 $\small k$ 有多个解:
$\small k_n=\frac{n\pi}{L}\ (n=1,2,3,\cdots) \quad\scriptsize{(式10.14)}$
所以方程的特解为一个三角函数序列:
$\small \psi_n(x)=A\sin{\left(\frac{n\pi}{L}x\right)} \ (n=1,2,3,\cdots) \quad\scriptsize{(式10.15)}$
在这里,系数 $\small A$ 还未确定,但这并不是那么重要,我们等一下再想办法确定它,而现在对我们来说,最重要的是找出能量的本征值。
根据前面的定义,我们有:
$\small k^2=\frac{2mE}{\hbar^2} \quad\scriptsize{(式10.16)}$
于是我们可以得到:
$\small E=\frac{\hbar ^2k^2}{2m} \quad\scriptsize{(式10.17)}$
而由于 $\small k$ 只能取一些分立值 $\small k_n=\frac{n\pi}{L}$ ,这就意味着能量也只能取分立值:
$\small E_n=\frac{n^2\pi^2\hbar ^2}{2mL^2} \quad\scriptsize{(式10.18)}$
这样,我们就得到了分立的能量本征值。
有了本征值,我们自然会想到相应的本征态。
显然,在这个问题中,能量的本征态,在坐标表象下,就是波函数的特解序列本身:
$\small \psi_n(x)=A\sin{\left(\frac{n\pi}{L}x\right)} \quad\scriptsize{(式10.19)}$
因为它作为定态薛定谔方程的解,天然满足定态薛定谔方程(这是句废话 )、也就是能量的本征方程:
$\small \hat{H}\left|\psi_n\right>=E_n\left|\psi_n\right> \quad\scriptsize{(式10.20)}$
而且,如果注意到 $\small \psi_n(x)=A\sin{(\frac{n\pi}{L}x)}$ 其实就是一个傅里叶级数序列,那么根据第7课中提到的性质,我们还可以验证不同的本征态 $\small \left|\psi_m\right>,\left|\psi_n\right>$ 之间的正交关系:
$\small \left<\psi_m|\psi_n\right>=\int_0^L{\psi_m\psi_n\text dx}=0\ (m\neq n) \quad\scriptsize{(式10.21)}$
这也是符合本征态组成的正交基底性质的。
到此为止,我们就完整复现了物理量算符的本征值关系,并且再次看到线性代数、微分方程、量子力学三者之间美妙的相似之处。
接下来,我们来看看前面还没确定的系数 $\small A$ 的取值。
3) 本征函数的归一化
在第6课中,我们曾经提到过,作为坐标表象下的态矢量的具体形式,任意一个波函数 $\small \psi(x) $,其实就以模方 $\small \left|\psi(x)\right|^2$ 的形式直接给出了粒子出现在位置 $\small x $的概率密度。
作为能量本征函数的$ \small \psi_n(x) $,也是一组特殊的态矢量,处于这些状态的粒子具有确定的能量,却具有不确定的空间位置分布,对应的概率密度为 $\small |\psi_n(x)|^2$ 。
在这个意义下,我们就能先求出本征函数前面的系数$\small A$ 了。
我们知道,在一维无限深势阱模型中,粒子只能出现在势阱区域内,这就意味着,无论粒子处于什么样的状态,我们在整个势阱区域内找到它的概率都是1,这叫做波函数的归一化。
将上面这句话写成数学表达式,就是:
$\small \int_{0}^{L}{|\psi(x)|^2\text dx}=1 \quad\scriptsize{(式10.22)}$
对于能量本征态,这个结论当然也成立,于是我们有:
$\small \int_{0}^{L}{A^2\sin^2{\left(\frac{n\pi}{L}x\right)}\text dx} =\frac{A^2L}{2}=1 \quad\scriptsize{(式10.23)}$
最终解得:
$\small A=\sqrt{\frac{2}{L}} \quad\scriptsize{(式10.24)}$
于是本征函数为:
$\small \psi_n(x)=\sqrt{\frac{2}{L}}\sin{\left(\frac{n\pi}{L}x\right)} \quad\scriptsize{(式10.25)}$
这样,我们就能画出$ \small n$ 取不同值时粒子在势阱中的概率分布函数 $\small |\psi_n|^2 $:
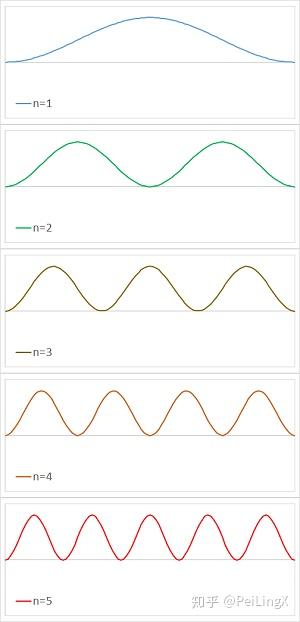
当然,对于这种过于理想化的一维无限深势阱而言,这些粒子位置概率分布图像并没有什么太适合的物理对应,并且从美学的角度来说也显得过于朴实无华而枯燥。
不过没关系,我们以后会欣赏到物理内涵更丰富、也更富有对称美的氢原子能级和能量本征态,那将是一次绝妙的精神体验。
而这节课的最后,我们要来简单、定性地解释一下为什么能级会分立。
前面我们只是笼统地知道,这是求解薛定谔方程的结果,但实际上,并不是所有量子力学模型都对应着分立能级,我们需要知道,分立能级什么条件下会出现。
4) 束缚态与能级分立
刚才求解一维无限深势阱时,也许有同学已经注意到,在粒子所在的势阱内,势能项变成0,薛定谔方程简化为没有势能项的形式:
$\small -\frac{\hbar^2}{2m}\frac{\text d^2}{\text d x^2}\psi=E\psi \quad\scriptsize{(式10.5)}$
这和我们第9课中提到的自由粒子(没有势能存在的环境中的粒子 )的薛定谔方程在形式上一模一样。
两个模型唯一的区别是,自由粒子所处的空间中整个空间中的势能都是0,而一维无限深势阱模型中,势能不为0的仅仅是有限的一段区域。
对于后者,我们知道,它的波函数的取值被限制在一段有限区间内,而我们在高数课上知道,这样的函数可以表示成傅里叶级数的形式(当然,它同时还要满足所谓的Dilichlet条件,但我们不必去关注这一点,因为我们讨论的所有波函数都满足它 )。
而我们求解薛定谔方程的结果也发现,它的特解就是一系列正弦函数,于是作为通解的一般波函数,就可以表示为这些特解的线性和,这正好就是傅里叶级数(也就是作为基底的能量本征态的坐标表象 ):
$\small \begin{align} \psi(x)&=\sum_n c_n\psi_n(x)\\ &=\sum_n c_n \sqrt{\frac{2}{L}}\sin{\left(\frac{n\pi}{L}x\right)} \end{align} \quad\scriptsize{(式10.26)}$
(当然,这个傅里叶级数比较特殊的一点是,它的余弦项系数全部为0,我们知道这是由边界条件决定的,而从态矢量的角度来讲,这就意味着无限深势阱中的波函数可以仅仅由一部分基底线性表出,也就是这样的边界条件决定了,这些波函数构成的是所有能够傅里叶展开的函数空间的一个子空间 )
现在我们来看自由粒子。
对于自由粒子而言,我们同样可以用能量本征态(同时也是动量本征态,正如我们在第9课中讨论的一样 )来作为一组基底,但由于此时没有边界条件的束缚,它的波数以及频率的取值就没有取整的限制,可以是任意实数,相应的能级也就是连续的了。
所以,对于上面两个例子体现出来的一些规律,我们可以给出一个笼统的一般表述:
对于取值被“限制在一定空间范围内的”波函数、或者更准确说是在无穷远处收敛的波函数,即满足 $\small \psi(\infty)=0$ 的函数,它的能级是分立的,这样的状态叫做束缚态;
反之,对于无穷远处不收敛的波函数,能级则是连续的,这样的态叫做散射态。
此外,还有一类不属于上面两种情况的模型,就是满足所谓周期性边界条件的波函数,它们在无穷远处不收敛,但能级也可能是分立的。这其实比较好理解,因为周期函数是可以分解成离散的傅里叶级数和、而不是连续的傅里叶变换的 (某种意义上,氢原子分立能级的来源可以等效成这样的情形,此外,如果同学们有机会学习固体物理,会体会到这一点 )
但上面说到的也还只是个结论,接下来,我们就分别从数学和物理的角度,来定性地解释这种区别。
- 数学上的定性解释
我们知道,定义在实轴上的所有函数可以构成一个无穷维的函数空间,而满足束缚态条件的波函数只是这些函数中的一个子集,而这个子集正好还构成了函数空间的一个子空间。
而我们在线性代数中知道,一个线性空间的子空间可以由一组基底的其中一部分(而不是全部 )张成。
对应到波函数中,如果我们选取所有能量值对应的能量本征态作为基底,那么波函数只在某个子空间中取值,就意味着,表述这个波函数时,只需要用到所有能量本征态当中的一部分(而不是全部 ),而这一部分本征态恰好就是那组分立的本征态,相应的能级自然也就是分立能级了。
当然,这只是一种定性解释,真正严谨的解释需要涉及到泛函分析的内容,这超出了我们这个系列的讨论范围(也超出了作者的能力范围 )
- 物理上的定性解释
我们先来看一个与量子力学无关的模型:一根具有弹性的弦。
如果将弦的两端固定,它就成了一根琴弦。
如果我们去了解一点音乐物理知识,我们会知道,拨动一根琴弦时,它发出的声音并不是一个单独的频率,而是一些不同频率的泛音的合成,但所有这些泛音的频率都是某个基频的整数倍。
这些泛音频率的倍数关系是怎么来的呢?
这就和我们的一维无限深势阱波函数很像了:
琴声中包含的每一个泛音频率,其实都一一对应了琴弦上的一个驻波模态。
我们知道,一段两端固定的琴弦上会形成驻波,而“两端固定”这个边界条件决定了,每个驻波模态的波长只能是琴弦长度的半整数分之一,而如果结合琴弦的波动方程,我们就能得到每个驻波模态的频率和波长的一一对应关系。
(对求解过程有兴趣的同学可以移步作者的这篇文章:律动的琴弦 )
对应到无限深势阱中的能级,我们其实就可以认为,是这样的边界条件导致波函数形成了驻波,这些驻波就是分立的能量本征态、而对应的频率就是能量的本征值、也就是能级本身了。
5) 结语与预告
本课里,我们动手求解了一种最简单的势能条件下的定态薛定谔方程,体验了如何通过求解方程找出能量本征值及本征态,并且定性解释了分立能级的来源,由此再次看到了微分方程、量子力学与线性代数之间的神似之处。
至此,我们关于薛定谔方程的这条主线就算介绍完了,接下来,我们要来解释第1课开篇中提到的另外一个让初学者很困惑的结论:不确定性原理。
在第3课和第5课中我们对此已经有了一些体会,而接下来我们要做的,是讨论量子力学中最重要的一对不确定性关系:坐标和动量的不确定性关系。
我们将仍然从态矢量的角度来理解,看看态矢量如何将这条主线也串起来:
编辑于 2021-12-06 11:48
