物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》的第5课。
了解本系列其他文章,请收藏目录:
0) 前情提要
在本系列的前3课中,我们通过几个虚构的思想实验,理解了量子力学特有的叠加态,并对不确定性原理进行了一次初体验。
而在第4课中,我们来到了真实的物理世界,回顾了量子力学史上最重要的实验之一:斯特恩-盖拉赫(Stern-Gerlach)实验(以下简称SG实验 )。
这个实验通过对银原子磁矩的探测,向我们展示了量子叠加态的真实存在。
但第4课介绍的,还仅仅是SG实验的“单机版”,而本文将继续介绍SG实验更为精彩的“联机版”:级联SG实验。
我们会发现,两个或多个SG实验装置串联到一起之后,会有更神奇的现象发生。

1) 级联SG实验:版本1.0
我们知道,单机版SG实验中,银原子分成了上下两束,说明测量银原子 $\small z$ 方向自旋时,原本处于叠加态的银原子状态,随机落到了两个本征态上。
我们将自旋磁矩为 $\small +z$ 方向和 $\small -z$ 方向的银原子所在的本征态分别记为 $\small \left|z_+\right> $ 和 $\small \left |z_- \right> $
现在,我们将原来单机版实验装置中的接收屏撤掉,让其中处于 $\small \left|z_+\right>$ 态的银原子(也就是向上走的那一束银原子 )继续往前走。
接下来,我们在这束银原子的前进方向上,放置另一个一模一样的SG实验装置,这个装置仍然具有沿着 $\small z $方向变化的磁场(后文中,我们将 $\small z$ 方向变化磁场的SG装置记为 $\small \text{SG}_z $)。
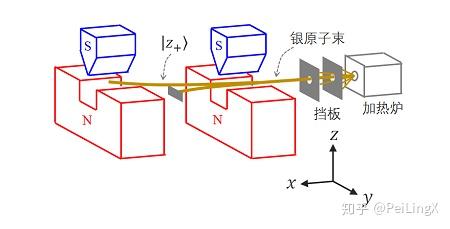
为了方便表示,我们将上述实验装置化成抽象图:
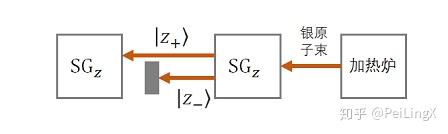
现在问题来了:这束 $\small \left|z_+\right>$ 的银原子通过这个新的 $\text{SG}_z $装置后,它还会不会分成两束?
经典直觉告诉我们:这束银原子具有确定的磁矩方向,即 $\small +z $方向,所以它们通过第二个 $\small \text{SG}_z$ 装置时,依然会向上偏转。
而事实的确也是如此。
(就像我们在第3课的量子糖思想实验中看到的那样,当我们尝了一次量子糖的味道之后,只要闭上眼睛不去观察它的颜色,那么无论我们多少次将量子糖放进嘴里重复品尝,它的味道都不会变 )
只不过,这里所说的“确定的磁矩方向”,其实已经不是经典意义上的“确定”了,而应该从叠加态的角度去解释。
我们在第4课中已经知道,当我们去测量银原子在 $\small z$ 方向的自旋磁矩时,随机得到的两个结果,就是这个“ $\small z $方向自旋磁矩”对应的两个本征态,即$\small \left|z+\right>$ 和 $\small \left|z-\right>$
而我们在第1课就已经知道,一个对象的任意量子态,都可以表示成某个物理量对应的一组本征态的叠加。
用线性代数语言来说就是:任意向量都可以表示成某个线性算子的一组完备特征向量(也就是一组完备基底)的线性组合。
所以,银原子的任意量子态 $\small \left|\psi\right>$ ,也都可以表示成两个本征态的叠加:
$\small \left|\psi\right>=k_{z+}\left|z_+\right>+k_{z-}\left|z_-\right> \quad\scriptsize{(式5.1)}$
其中两个系数满足:
$\small \left|k_{z+}\right|^2+\left|k_{z-}\right|^2=1 \quad\scriptsize{(式5.2)}$
这对本征态本身也成立,比如对于处于 $\small \left|z_+\right> $的银原子,它的状态就是:
$\small \left|z_+\right>=1\left|z_+\right>+0\left|z_-\right> \quad\scriptsize{(式5.3)}$
而根据我们在第2课中看到的系数的物理含义可知,系数的模方 $\small \left|k_{z+}\right|^2$ 和 $\small \left|k_{z-}\right|^2$ 分别对应着测量 $\small z $方向自旋磁矩时、得到结果 $\small \left|z_+\right>$(即SG实验中向上偏转的银原子 )和 $\small \left|z_-\right>$ (SG实验中向下偏转的银原子 )的概率。
于是,对于已经处于本征态 $\small \left|z_+\right>$ 的银原子而言,当我们再去测量它在 $\small z $方向上的自旋磁矩时,它继续坍缩到本征态 $\small \left|z_+\right>$ 的概率就是1,而变成本征态 $\small \left|z_-\right>$ 的概率就是0。
体现在实验中就是:原来向上偏转的银原子束,通过第二个 $\small \text{SG}_z $装置后,仍然全部向上偏转,没有例外。
有了这种叠加态的思维,我们才能比较顺畅地理解下一个版本的联机实验。
2) 级联SG实验:版本2.0
这是级联SG实验中最重要的一个版本。
在这个版本中,我们将再次看见不确定性原理的影子。
首先,我们仍然从单机版的 $\small \text{SG}_z $ 装置中筛选出 $\small \left|z_+\right>$ (自旋磁矩为 +z 方向 )的银原子,并且撤去接收屏,让这束银原子通过一个通过磁场沿 $\small y $方向的SG实验装置,记为$ \small \text{SG}_y$
实验的抽象图如下:
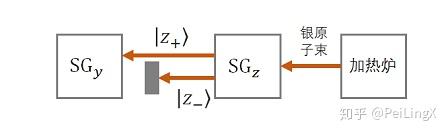
接下来,请各位猜一猜:处于 $\small \left|z_+\right>$ 状态的银原子,通过 $\small \text{SG}_y $装置后,会发生什么事情?
按照经典直觉,进入磁场的银原子具有确定的磁矩方向 $\small +z $,而 $\small \text{SG}_y$ 装置中,磁场方向以及变化方向都是 $\small y$ 方向,磁矩 $\small \boldsymbol\mu$ 和磁感应强度梯度方向的夹角 $\small \frac{\pi}{2}$ ,于是银原子受到的磁场力大小为:
$\small F=\mu_z\frac{\partial B_y}{\partial y}\cos{\frac{\pi}{2}}=0 \quad\scriptsize{(式5.4)}$
这意味着,银原子会在$ \small \text{SG}_y $装置的磁场中直来直去,不发生在 $\small y $方向上发生任何偏转。
但实际结果却是,银原子又分裂成了两束,一束朝 $\small +y$ 方向偏转,另一束朝 $\small -y $方向偏转!

也就是说,原本自旋磁矩处于 $\small +z$ 方向的银原子,通过 $\small \text{SG}_y $装置后,自旋磁矩方向发生了惊天大转弯,变成了 $\small +y$ 或 $\small -y$ 中的一个。
并且,如果我们将 $\small \left|y_+\right> $ 和 $ \small \left|y_-\right> $两束银原子的数量分别数一遍,会发现它们大致相等。
是的,这必须又要用叠加态来解释了。
我们知道,“ $\small z $方向磁矩”具有两个本征态 $\small \left|z_+\right>$ 和 $\small \left|z_-\right>$ ,而“测量 $\small y$ 方向磁矩”也有两个本征态 $\small \left|y_+\right>$ 和 $\small \left|y_-\right>$ ,也就是银原子束通过 $\small \text{SG}_y $后分裂成的两束分别对应的量子态。
于是,我们可以将版本2.0的SG实验结果转换成量子语言:
对 $\small \left|z_+\right>$ 态的银原子,如果去测量它的 $\small y$ 方向磁矩,那么银原子的状态会随机坍缩到 $\small \left|y_+\right> $和 $\small \left|y_-\right>$ 中的一个;
而 $\small \left|y_+\right>$ 和 $\small \left|y_-\right>$ 两束银原子的数量大致相等,就意味着,对 $\small \left|z_+\right>$ 态的银原子,测量 $\small y$ 方向磁矩时,坍缩到$ \small \left|y_+\right> $和 $\small \left|y_-\right>$ 的概率是相等的。
还记得我们在第3课的量子糖思想实验中,交替进行“看颜色”和“尝味道”两种行为时,发生的事情以及我们的解释吗?
(不记得的同学,建议先复习第3课内容 )
在这个级联SG实验中,我们可以将“测量 $\small z$ 方向自旋磁矩”类比为“观察量子糖的颜色”,将“测量 $\small y$ 方向自旋磁矩”类比为“品尝量子糖的味道”。
根据量子糖思想实验中的解释方式,我们可以推知: $\small z $方向自旋磁矩处于确定的本征态时,$ \small y $方向自旋磁矩就处于不确定的叠加态 (这里又一次看到了不确定性原理的影子 )。
换句话说就是:“$ \small z$ 方向自旋磁矩”对应的本征态,是“ $\small y $方向自旋磁矩”对应的本征态的线性叠加。
这才是这次级联SG实验结果的正确打开方式。
而根据“ $\small \left|z_+\right> $态的银原子坍缩到 $\small \left|y_+\right>$ 和$\small \left|y_-\right> $的概率相等”这条线索,我们还能推知,将 $\small \left|z_+\right>$ 表示成$ \small \left|y_+\right>,\left|y_-\right>$ 的线性叠加时,系数的模方也是相等的。
于是我们可以进一步猜出它们之间的一种可能的关系:
$\small \left|z_+\right>=\frac{1}{\sqrt{2}}\left|y_+\right>+\frac{1}{\sqrt{2}}\left|y_-\right> \quad\scriptsize{(式5.7)}$
同时也可以得到:
$\small \left|z_-\right>=-\frac{1}{\sqrt{2}}\left|y_+\right>+\frac{1}{\sqrt{2}}\left|y_-\right> \quad\scriptsize{(式5.8)}$
根据这个关系,我们还可以看出,两组本征态在态空间中的“夹角”是45度。
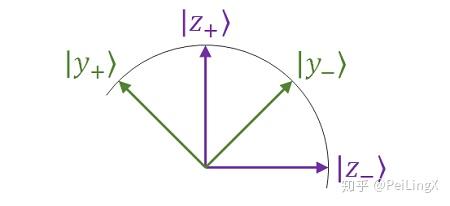
而我们知道,在“真实物理空间”中, $\small z$ 方向磁矩和 $\small y$ 方向磁矩的夹角是90度。
于是我们又一次看到了在第4课中提到的自旋磁矩“在真实物理空间中的夹角 $\small \theta $”与“在态空间中的夹角 $\small \varphi$ ”之间的倍数关系: $\small \theta=2\varphi$
至于这背后是否有更精妙的数学结构,要到比较遥远的以后再揭晓答案了。
现在我们先记住这个关系就行。如果担心自己记不住,不妨来做个随堂练习巩固一下:
【练习5.1】
假设一个级联SG实验中,第一个装置是 $\small \text{SG}_z$ ,第二个装置的磁场方向再不是 $\small y $,而是$ \small yz$ 平面内一个与$ \small z$ 成 $\small \theta$ 角的方向,将该装置记为 $\small \text{SG}_\theta$ (如图)。银原子通过 $\small \text{SG}_z$ 后分成两束,我们筛选出 $\small \left|z_+\right> $对应的那束银原子,让它们通过 $\small \text{SG}_\theta$ ,并再次分裂成两束,问:通过 $\small \text{SG}_\theta$ 后的两束银原子中,向上偏转和向下偏转的银原子数量占比分别大约是多少?
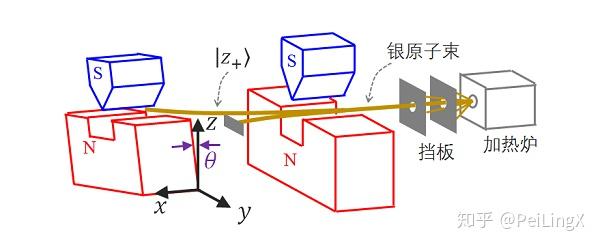
(答案在文末附录中 )
暂时不想算的同学,可以跟着作者进入下一个版本的级联SG实验,它没有第二个版本那么烧脑,但依然很有意思。
3) 级联SG实验:版本3.0
这是一个有关“前世记忆”的实验,它是这样操作的:
先让银原子通过一个 $\small \text{SG}_z$ 装置,从中筛选出 $\small \left|z_+\right> $那束银原子,让它们通过一个 $\small \text{SG}_y$ 装置,然后从中又筛选出 $\small \left|y_+\right>$ 的银原子,让它们再次通过一个 $\small \text{SG}_z $装置。
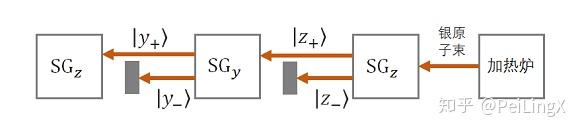
这样做是为了看看这些银原子是否还“记得”自己在上次通过 $\small \text{SG}_y$ 前,“曾经”是 $\small \left|z_+\right>$ 。
已经有了量子思维的我们,可以很快得出结论:
通过第二个 $\small \text{SG}_z $装置的银原子,将会再次均匀分裂成两束,因为它们进入第二个 $\small \text{SG}_z$ 装置前,已经处于 $\small \left|y_+\right>=\frac{\sqrt{2}}{2}\left|z_+\right>-\frac{\sqrt{2}}{2}\left|z_-\right> $ 的状态。
也就是说,通过 $\small \text{SG}_y $后落到 $\small y $方向自旋本征态的银原子,就像喝了一碗孟婆汤,忘却了它“前世是 $\small \left|z_+\right>$ ”的记忆,在再次通过 $\small \text{SG}_z$ 时,重新随机选择了自旋磁矩的本征态。
是的,量子世界就是这么绝情却又让人着迷。
4) 结语和预告
通过第4课和第5课的介绍,我们完整地看到了一例发生在真实物理世界中的量子叠加现象,并且再次感受到了不确定性原理的影子。
但“自旋”这个概念还是离我们的经典世界比较遥远,而我们在第1课开头提出的那些疑惑还几乎都没得到解答。
但没关系,通过这几节课的发酵,现在我们已经对态矢量以及它的物理意义有了一点感觉,并且能够通过线性代数在脑中形成关于它的几何图景。
从第6课开始的很长一段旅程里,我们就要用这些刚刚形成的认识,去解开一个个谜团了。
而在进入下一个主题之前,我们还要趁热打铁,利用本课刚刚新鲜出炉的“自旋”的量子性质,来理解量子力学在信息学中的一个重要应用:量子加密。
它的一个最原始也最简单的版本,是一种不可被伪造的货币:量子货币。
欲知详情,请移步番外编:
附录:
练习5.1答案:
向上偏转( $\small \left|\theta_+\right>$ )的银原子占比为 $\small \cos^2{\frac{\theta}{2}} $;向下偏转( $\small \left|\theta_-\right>$ )的银原子占比为$ \small \sin^2{\frac{\theta}{2}}$
(有两位同学同时最先给出正确答案:Andy, RD巨佬;回头会送上小礼物~ )
编辑于 2021-11-30 13:22
