fmingde
版次: 2024
了解本系列其他文章,请浏览目录:
《大学物理》内容提要目录
§5 真空中静电场
一、库仑定律、静电场、电场力
1. 电荷守恒定律
在一个孤立的带电系统中,无论发生什么变化,系统所具有的正负电荷电量的代数和保持不变。
2. 真空中的库伦定律 $\vec F =\cfrac 1 {4\pi \varepsilon_0}\cfrac {q_1q_2}{r^2}\vec e_r$
3. 静电场: 静止电荷产生的电场
(1)力学性质 - 电荷在电场中要受到电场力的作用
(2)能量性质 - 电场力对电荷有作功的本领
4. 电偶极矩 $\vec p=q\vec r_0$

二、电场强度、场强叠加原理
1. 电场强度 $\vec E$
(1)定义 $\vec E=\cfrac {\vec F} {q_0}$
$q_0$:试验电荷,是正的点电荷;电量足够小,不影响被试验的电场。
电场强度是空间位置的矢量函数:$\vec E(x,y,z)$ ,或 $\vec E(\vec r)$
(2)图示: 电场线
(3)点电荷的电场强度 $\vec E =\cfrac 1 {4\pi \varepsilon_0}\cfrac q{r^2}\vec e_r$
具有球对称性,相同$r$ 上大小相等,方向沿 $\vec r$
2. 电场强度的叠加原理
(1)电荷离散分布时: $\vec E=\sum \limits_i \vec E_i= \sum \limits_i \cfrac 1 {4\pi \varepsilon_0 }\cfrac {q_i} {r_i^2}\vec e_{ri}$
某点的场强,等于各点电荷在该点产生的场强的矢量和
(2)电荷连续分布时:$\vec E=\int d\vec E= \int \cfrac 1 {4\pi \varepsilon_0 }\cfrac {\vec e_r} {r^2}{\rm d}q$
某点的场强,等与各电荷元在该点产生的场强的矢量和
3. 常用结论(典型带电体的电场强度)
(1)有限长直导线附件的电场强度
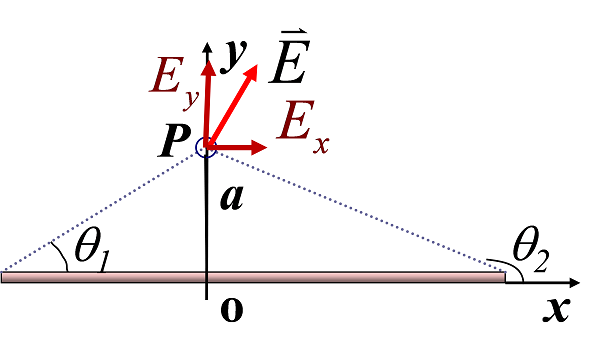
$E_x=\cfrac \lambda {4\pi\varepsilon_0 a}(\sin \theta_2 - \sin \theta_1)$
$E_y=\cfrac \lambda {4\pi\varepsilon_0 a}(\cos \theta_1 - \cos \theta_2)$
导出结论:
1)无限长带电直线的电场 (用高斯定理更好解释,见“三”)
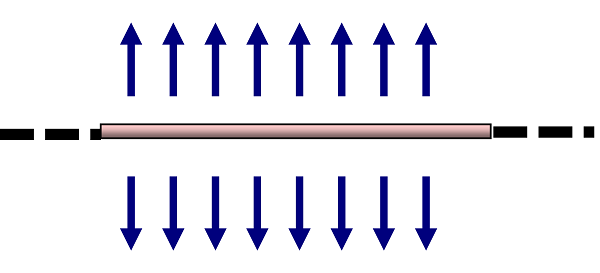
$E=E_y=\cfrac \lambda {2 \pi \varepsilon _0 a}$
2)半无限长直导线端面上的电场(45度向外)

$E_x=E_y=\cfrac \lambda {4 \pi \varepsilon _0 a}$
(2)均匀带点圆环轴线上的场强
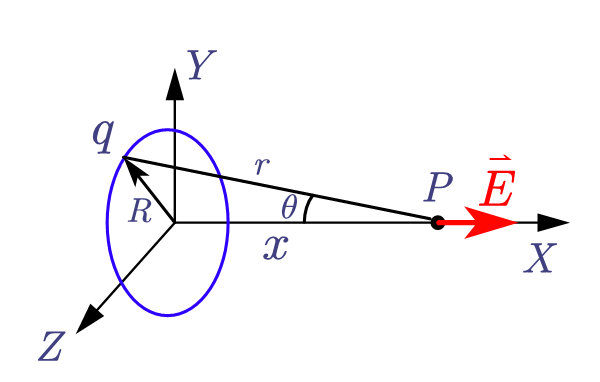
$\begin{align} E &=\cfrac q {4\pi \varepsilon_0 r^2}\cos \theta \\ &= \cfrac {qx} {4\pi \varepsilon_0 (x^2+R^2)^{\frac 3 2}}\end{align} $
计算要求:★★运用场强叠加原理,计算电场强度。1)积分叠加 2)由常用结论叠加
注意:矢量叠加,必要时按坐标系,先分量叠加。
典型习题:三、1,2
三、高斯定理及其应用
1. (真空中静电场的)高斯定理 ${\it \Phi}_e=\oint \limits_S \vec E \cdot {\rm d}\vec S=\cfrac 1 {\varepsilon_0} \sum \limits^n_{i=1}q_i $
在真空中,通过任一闭合曲面$S$的电场强度通量,等于该曲面所包围的所有电荷的代数的 $\cfrac 1 {\varepsilon_0}$倍
对高斯定理的理解:
1)高斯定理表达了场源(电荷)和场的空间分布之间的联系。
2)曲面$S$上各处的局部通量是所有电场共同形成(通量积分式中的 $\vec E$是所有电荷形成的电场的矢量和),闭合曲面上的总通量数值只取决于内部电荷数量(外部电荷,对闭合曲面的通量贡献为零)。
3)静电场是有源场(场线有起点,有终点)
2. 高斯定理的运用
1)求解具有对称性的静电场的场强;2)由场强分布判断电荷分布
3. 常用结论(典型带电体的电场强度)
(1)均匀带电球面的电场 – 选同心的球形高斯面后求得
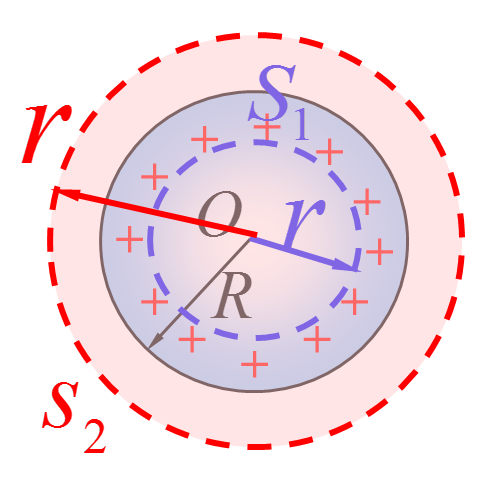
$E=\begin{cases} 0 & r<R \\ \cfrac q {4\pi\varepsilon_0 r^2} & r>R \end{cases}$
(2)无限长均匀带电直线的电场 – 选圆柱形高斯面后求得
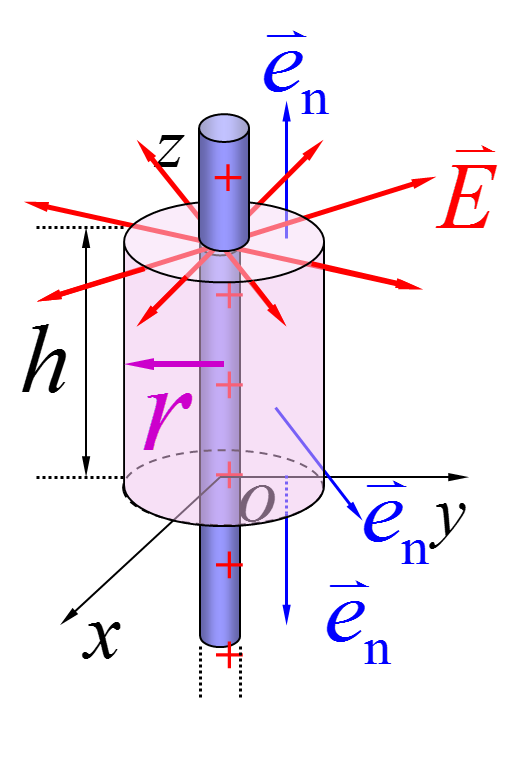
$E=\cfrac \lambda {2\pi\varepsilon_0 r}$
(3)无限大均匀带电平面的电场 – 选圆柱形高斯面后求得
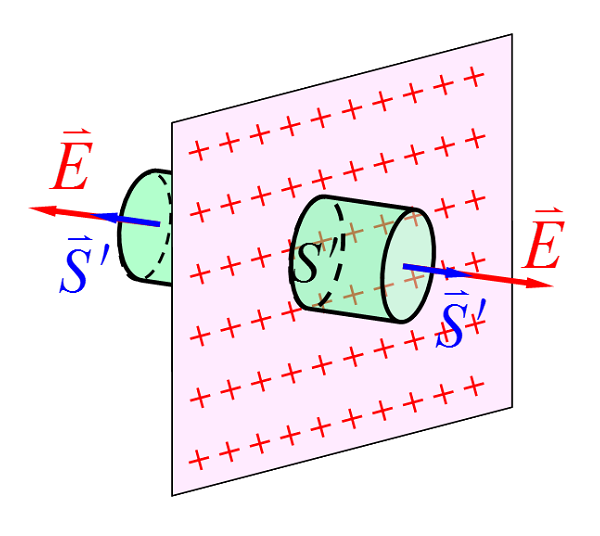
$E=\cfrac \sigma {2\varepsilon_0}$
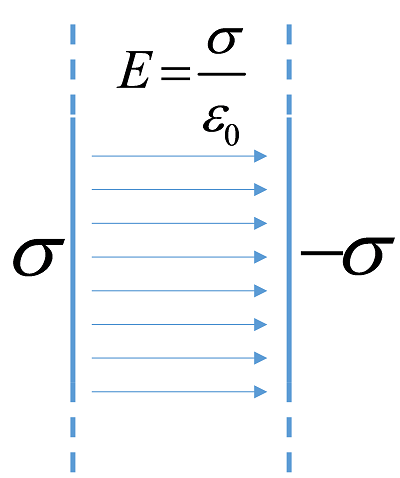
(4)$n$个无限大平行带电平面 – 各区域都是$n$项叠加
典型情景:等量异号带电的两个无限大平面,电场存在与两面之间,大小为$E=\cfrac \sigma {\varepsilon_0}$
计算要求:★★★用高斯定理计算场强分布
1)球对称电场,选同心球面为高斯面; 2)柱对称电场,选同轴圆柱面为高斯面;3)面对称电场,选圆柱面,圆柱底面与场线垂直。
若包含介质,应该用“含介质时的高斯定理”
典型习题:三、3
四、静电场的环路定理
$\oint_l\vec E\cdot {\rm d}\vec l=0$
说明静电场是保守场
是电势能、电势等概念的依据
五、电势、电势叠加原理
1. 电势能
试验电荷$q_0$在某点的电势能,等于从该点出发,移动$q_0$到势能零点时,电场立所作的功。(电势能转化为静电场力作功).
$E_{pA}=\int^{\text{势能零点}}_A q_0\vec E \cdot {\rm d}\vec l$
2. 电势
(1)定义 $V_A=\cfrac {E_{pA}} {q_0}$
$A$点的电势等于试验电荷在该点的电势能与试验电荷的电量的比值
$A$点的电势在数值上等于把单位正电荷从A点移到电势零点处时,静电力所做的功
$V_A=\int^{V=0}_A\vec E \cdot d\vec l$
(2)图示: 等势面
(3)电势差 $U_{AB}=V_A-V_B$
(4)点电荷的电势 $V=\cfrac q {4\pi\varepsilon_0r}$
是球对称分布的标量函数,只有大小。
3. 电势的叠加原理
(1)多个离散电荷时: $V_P=\sum \limits_i V_{Pi}=\sum \limits_i \cfrac {q_i} {4\pi\varepsilon_0 r_i}$
$P$点的电势等于各点电荷单独存在时,在$P$点的电势之代数和
(2)电荷连续分布时: $V_P=\int \cfrac {{\rm d}q} {4\pi\varepsilon_0r}$
$P$点的电势等于各电荷元在$P$点的电势之代数和
4. 电势的计算方法
(1)采用电势叠加原理
点电荷电势的叠加
电荷元电势的叠加(积分)
已知结论的叠加
计算要求:★★★用电势叠加原理计算电势分布
典型习题:三、5
(2)定义法 $V_P=\int^{V=0}_P\vec E \cdot {\rm d}\vec l$
求$P$点的电势,可选连接$P$点和势能零点的一条路径(曲线$l$),沿路径计算电场强度(分量)对路径的积分值。
一般取过$P$点的电场线为路径,积分即可。
计算要求:★★用场强分布积分计算电势
典型习题:三、6
六、场强分布和电势分布的关系
(1)已知场强分布,可知任意点电势值: $V_P=\int^{V=0}_P\vec E \cdot {\rm d}\vec l$
(2)已知电势分布,可知任意点电场强度: $\vec E=-\nabla V$
已知电势分布,可知电场强度沿方向$l$的分量 $E_l=-\cfrac {\partial V} {\partial l}$
§6 静电场中导体和电介质
一、静电场中的导体: 静电感应和静电平衡
导体中存在大量能自由移动的负电荷,在外电场中,将根据需要进行快速移动,达到平衡。主要掌握平衡后正负电荷的静分布,及这些电荷形成的电场。
1. 导体的静电平衡条件
(1)以电场强度表示
1)导体内部任何一点处的电场强度为零($E_{\text{内}}=0$ )
2)导体表面处的电场强度的方向,都与导体表面垂直( $E_{\text{表面}} \bot $导体表面)
(2)以电势表示
导体是个等势体,导体表面是个等势面。
2. 导体表面电场强度与电荷面密度的关系 $E=\cfrac \sigma {\varepsilon_0 }$
表面电场强度的大小与该表面电荷面密度成正比
3. 静电屏蔽
空腔导体可以屏蔽外电场
接地空腔导体将使外部空间不受空腔内的电场影响
4. 典型问题:平行金属板表面电荷的分布
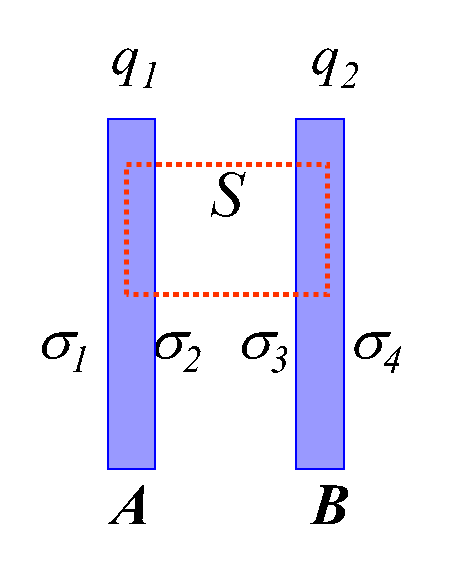
$\sigma_1=\sigma_4=\cfrac {q_1-q_2}{2S}$
$\sigma_2=-\sigma_3=\cfrac {q_1-q_2}{2S}$
外侧表面上电荷等量同号
内侧表面上电荷等量异号
5. 导体静电平衡问题中的其他注意事项
接地: 强迫电势为零,在电势变化到零的过程中,有电荷移动。 多个导体时,其中一个接地,各个导体的电势都发生变化。
计算要求:★★判断导体表面电荷的分布情况
结合: 1)高斯定理 2)电荷守恒定律
典型习题:一、1
计算要求:★★★导体球、柱等组合后,场强分布、电势分布的计算
1)应用高斯定理,求各层场强
2)选择合适的直线路径,积分计算电势分布
典型习题:三、6,7
二、静电场中的电介质:极化现象
1. 电介质的极化
1)无极分子产生位移极化,有极分子产生取向极化;2)极化强度矢量定义: $\vec P=\cfrac {\sum \vec p_i}{\Delta V}$;3)极化后产生额外的束缚电荷。
2. (各向同性)介质中电场强度
$E=\cfrac {E_0} {\varepsilon _r}$ $\varepsilon_r$:介质的相对介电常数
三、含介质时的高斯定理、环路定理
1. 电位移矢量 $\vec D=\varepsilon\vec E$
综合反映电场强度和极化现象的物理量
1)一般定义: $\vec D=\varepsilon_0\vec E+\vec P$
2)对各向同性介质,简化为 $\vec D=\varepsilon\vec E$ $\varepsilon$:介质的介电常数(电容率), $\varepsilon =\varepsilon_0\varepsilon_r$
2. 含介质时的高斯定理 $\oint_S\vec D \cdot {\rm d}\vec S=q_0$
在静电场中,通过任意闭合曲面的电位移通量等于该闭合曲面内所包围的自由电荷的代数和
计算要求:★★★用高斯定理计算场强分布
同上一章高斯定理,含介质时,选用
典型习题:
三、电容器的电容
1. 电容(量)的定义
(1)对孤立导体: $C=\cfrac Q V$
(2)对电容器 $C=\cfrac Q {V_A-V_B}=\cfrac Q U$
电容的大小仅与导体的形状、相对位置、其间的电介质有关. 与所带电荷量无关.
计算要求:★★电容器电容的计算
2. 电介质对电容器的影响
$C=\varepsilon _rC_0$
填充介质后,电容量增加。(上式仅适用于介质完整填充,其他情形需具体计算)
3. 平行板电容器的电容
$C=\varepsilon \cfrac S d$ $S$:极板面积, $d$:极板间距
4. 电容器联接
(1)并联: $C=\sum C_i$
各电容具有相同的端电压,能增大总电容
(2)串联: $\cfrac 1 C=\sum \cfrac 1 {C_i}$
各电容具有相同的储电量,能提高耐压能力
5. 电容器储存的电能
计算要求:★★★平行板电容器的综合问题
1)插入导体板;2)插入介质板;3)储能;4)插入极板过程中的功。
典型习题:三、3,4
四、电场的能量
1. 电场能量密度 $w_e=\cfrac 1 2ED=\cfrac 1 2 \varepsilon E^2$
2. 电场的能量 $W_e=\int_Vw_e{\rm d}V=\int_V \cfrac 1 2\varepsilon E^2{\rm d}V$
计算要求:★场能量的积分计算
典型习题:三、5
