fmingde
版次: 2024
了解本系列其他文章，请浏览目录：
《大学物理》内容提要目录

§9 振动

一、简谐运动

1. 简谐振动的特征

　　动力学特征：$F=-kx$
　　运动学特征：$\cfrac {{\rm d}^2x}{{\rm d}t^2}+\omega^2x=0$
　　　　运动方程: $x=A\cos(\omega t+\varphi)$
　　能量特征: $E=E_k+E_p=\cfrac 1 2kA^2$

计算要求：★判断一个物体的运动是否为简谐振动；若是，建立简谐运动方程

2. 速度和加速度

　　$v=\cfrac {{\rm d}x} {{\rm d}t}=-\omega A \sin(\omega t+\varphi)$ $v_m=\omega A$
　　$a=\cfrac {{\rm d} ^2 x}{{\rm d}t^2}=-\omega ^2A \sin(\omega t+\varphi)$ $a_m=\omega^2A$

3. 描述简谐振动的特征量

（1）周期、频率、圆频率，由振动系统本身的性质所决定
$\omega=2\pi\nu=\cfrac {2\pi} T$

　　　　弹簧振子：$\omega=\sqrt{\cfrac k m }$
　　　　单摆：　　$\omega=\sqrt{\cfrac g l }$
　　　　复摆：　　$\omega=\sqrt{\cfrac {mgl} J }$

（2）振幅$A$，初相位$\varphi$ , 由初始条件决定
　　$\left. \begin{array}{l}
x_0=A\cos\varphi \\ v_0=-A\omega\sin\varphi \end{array} \right\}
\Rightarrow \left\{ \begin{array}{l}
A=\sqrt{x_0^2+(\cfrac {v_0} \omega)^2} \\ \tan\varphi=-\cfrac {v_0}{\omega x_0} \end{array} \right.$

　　（不用记右方两式，列出左边两式后解出）

计算要求：★★联系谐振动的运动方程、初始值和振动曲线解决有关问题
　　　　　1）由运动初始条件或振动曲线，确定运动方程；2）由振动系统参数(质量等)确定振动周期，写出运动方程；3）由运动方程讨论速度、能量等特征
典型习题：三、2, 3

4. 表示方法

（1）数学解析法：运动方程 $x=A\cos(\omega t+\varphi)$

（2）旋转矢量图示法
　　任何一个简谐运动都可看作是一个旋转矢量在振动方向上的投影。可借助旋转矢量矢端的圆周运动来理解简谐振动中各物理量:
　　　　

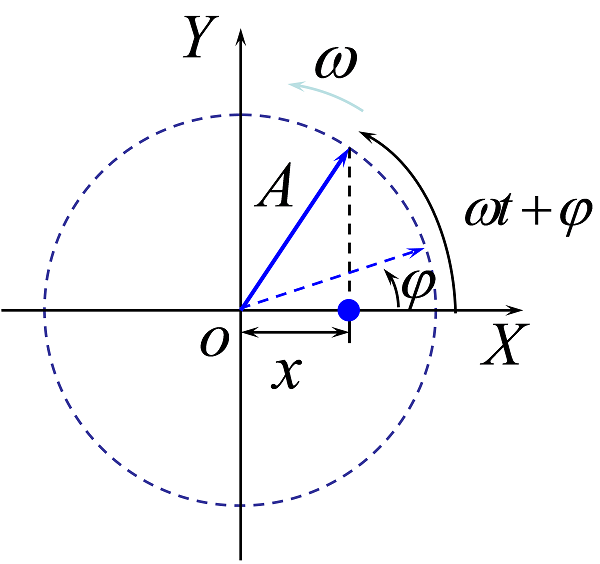
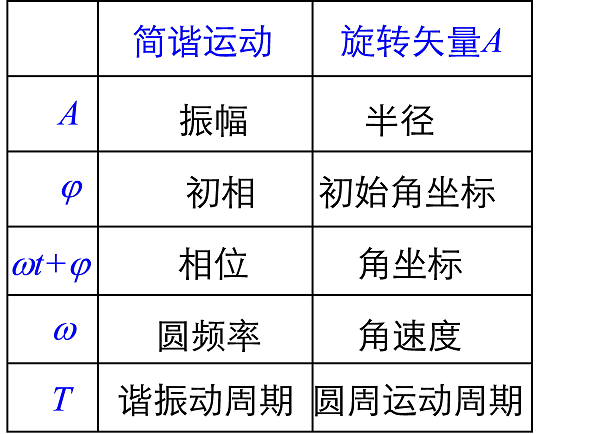
　　利用旋转矢量可快速判断振动的曲线图示
　　利用旋转矢量，可由初始条件确定初始相位的取值区间
　　利用旋转矢量，可快速判定两振动状态之间的时间差

计算要求：★★借助旋转矢量法，可简化相位关系的分析过程

（3）时间-位移曲线
　　

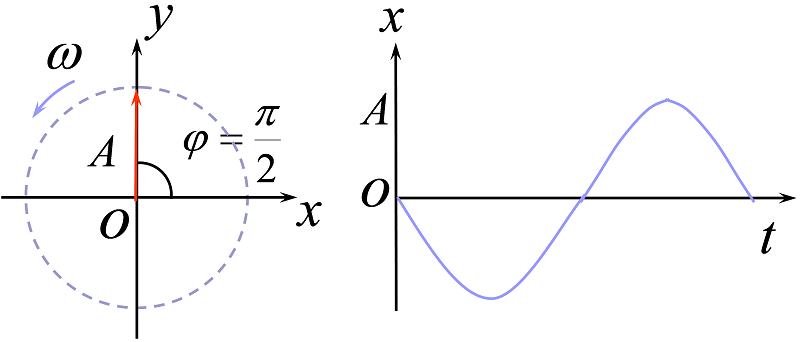
　　左图为初始时刻旋转矢量，当其按角速度$\omega$旋转时，按时刻将矢量端点在$x$轴上的投影值在$x-t$图中描出，即为时间-位移曲线。

5. 简谐运动的合成

（1）同方向同频率两个简谐振动的合成 — 仍是简谐振动
　　分振动： $x_1=A_1\cos(\omega t+\varphi_1) $ 　　$x_2=A_2\cos(\omega t+\varphi_2)$
　　合振动： $x=A\cos(\omega t+\varphi)$
　　合振幅： $A=\sqrt {A_1^2+A_2^2+2A_1A_2\cos(\varphi_2-\varphi_1)}$
　　初相位： $\varphi =\arctan \cfrac {A_1\sin \varphi_1+A_2\sin \varphi_2}{A_1\cos \varphi_1+A_2\cos\varphi_2}$
　　或用旋转矢量法解决:
　　

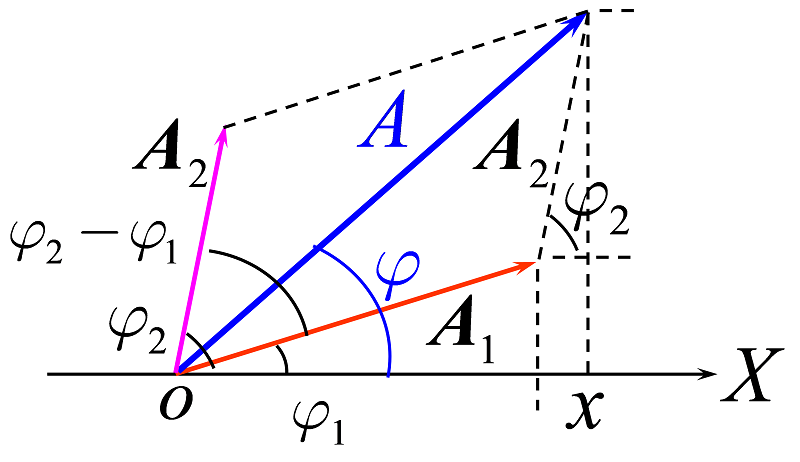
计算要求：★合振动的计算
典型习题：三、7 1)合振动的计算 2)振动加强、减弱条件

（2）同方向不同频率简谐振动的合成 — 不是简谐振动
　　当频率很大，但频差很小时，产生拍频现象。
　　拍频 $\nu=|\nu_2-\nu_1|$

（3）两个互相垂直的同频率简谐振动的合成 － 椭圆形运动
　　轨迹方程：
　　$\biggl (\cfrac x {A_1}\biggl )^2+\biggl (\cfrac y {A_2}\biggl )^2-\cfrac {2xy\cos(\varphi_2-\varphi_1)}{A_1A_2}=\sin^2(\varphi_2-\varphi_1)$

　　椭圆的性质（方位、长短轴、左右旋）在$A_1、A_2$确定之后, 主要决定于位相差$\Delta\varphi=\varphi_2-\varphi_1$ 。
　　$\Delta\varphi=0$或 $\Delta\varphi=\pi$ 时，椭圆轨迹退化为直线轨迹（椭圆短轴为$0$）

（4）两个互相垂直的不同频率简谐振动的合成
　　频率成整数比时，能形成稳定的利萨如图形。

二、阻尼振动、受迫振动和共振

（1）阻尼振动：振幅不断减小，能量不断损失。
　　相关概念：过阻尼、临界阻尼、弱阻尼。

（2）受迫振动：在驱动力作用下，系统发生的运动。
　　达到稳定状态后，振动频率为驱动力的频
　　共振：驱动力频率接近振动系统固有频率时，受迫振动振幅达到最大值。

§10 波动

一. 机械波

1. 产生的条件：波源与弹性介质

2. 描述波动的物理量

　　1）波长$\lambda$ ；2）周期$T$ (频率$\nu$ ) ；3）波速$u$
　　波长由介质决定；周期（频率）由波源决定。
　　三者关系： $u=\lambda\nu=\cfrac \lambda T$

二、平面简谐波

1. 平面简谐波的表达式（波函数、波动方程）

（1）若坐标原点振动方程为$y=A\cos(\omega t+\varphi)$ ，波向$x$轴正向传播，则波动方程为:
　　$\begin{align} y &=A\cos[\omega(t-\cfrac x u)+\varphi] \\ &=A\cos(\omega t-\cfrac {2\pi} \lambda x+\varphi)\\&=A\cos[2\pi(\cfrac t T-\cfrac x \lambda)+\varphi] \end{align}$

　　由来：1）$x$处重复的是原点O在$t-\cfrac x u$时状态
　　2）$x$处的振动相位较O落后(数值小) $2\pi\cfrac x \lambda$

此两条作为已知某点振动方程，写另一点振动方程，或波动方程的依据。

（2）已知某点振动方程，写出波动方程的方法：
　　1）时间回溯法：替换振动方程中$t$为$t-\cfrac x u$ 。
　　2）相位落后法：在振动方程中，相位减去 $2\pi\cfrac x \lambda$。
　　“距离”中出现坐标变量$x$。使振动方程$y(t)$提升为波动方程 $y(x,t)$。

建议用“相位落后法”。遵循“沿传播方向，相位落后”。
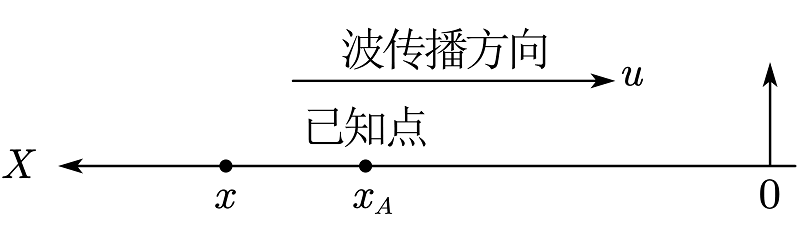
明确传播方向后，视坐标轴方向，任意假设一个$x$点(通常画在$x$正轴上)，若$x$点在已知点传播“前方”，则相位减 $2\pi \cfrac {\scriptstyle \text{距离}} \lambda$，若$x$点在已知点传播“后方”，则相位加 $2\pi \cfrac {\scriptstyle\text{距离}} \lambda$。“距离”始终按正值去表达。

例如:上图中传播方向向右，但坐标正方向取为向左，已知点A振动方程时: 在$x$轴正向上任意标取个$x$点，$x$点在传播方向“前方”,相位减去$2\pi \cfrac {x_A-x} \lambda $ 。

若$x$点被标记在了已知点左方，则x点在传播方向“后方”，相位加上$2\pi \cfrac {x-x_A} \lambda$ 。得到的波动表达式与前一情形相同（结果与画图时标注位置无关，尽量将$x$点标注在传播“前方”，以便运用”沿传播方向相位落后“）

计算要求：★★已知某点振动方程，写出波动方程。已知波动方程，写某点的振动方程。

典型习题：三、3 振动波动综合练习:三、2

2. 平面简谐波的波形图

　　一般仅能画出某一时刻$t$的“波形”曲线。
　　由当前波形曲线，想象经过小段时间$\Delta t<<T$后的波形，能判断各点的振动方向
　　考察坐标原点的当前位移和振动方向，能判断$t$时刻相位$\omega t+\varphi$ 。

3. 平面简谐波的能量

（1）能量传播特点

　　1）任一时刻介质质元的动能等于势能，且相位相同。
　　在平衡位置时质元具有最大动能和势能，在振幅处动能和势能为零。

　　2）体积元总能量随时间作周期性变化，机械能不守恒。
　　波动过程中，沿波的传播方向，质元不断地通过振动由“上游”的质元获得能量，又不断地把能量传播给“下游”的质元。

（2）平均能流
　　单位时间内垂直通过介质中某一面积的能量。
　　$\overline P=\cfrac 1 2\rho A^2\omega ^2\cdot uS$

　　其中$\cfrac 1 2\rho A^2\omega ^2$为平均能量密度(对时间平均后的单位体积内的能量）
　　$u$为波速、$S$ 为垂直截面面积。
　　平均能流类似“功率”，单位为$\rm W$(瓦)

（3）能流密度(波的强度)
　　单位时间、垂直通过单位面积的能量，衡量波强弱的物理量。
　　$I=\cfrac {\overline P}{S}=\overline w\cdot u=\cfrac 1 2\rho A^2\omega^2\cdot u$

　　波的强度正比于振幅的平方。

三、惠更斯原理和波的叠加原理

1. 惠更斯原理

2. 波的叠加原理

3. 波的干涉

（1）现象 － 几列波叠加形成的强度的稳定分布的现象。
（2）相干条件
　　振动方向相同、频率相同、相位相同或相位差恒定
（3）干涉相长和干涉相消的条件
　　1）取决于两分振动的相位差 $\Delta \varphi=-2\pi \cfrac {r_2-r_1} \lambda$
　　 　　$\varphi_2-\varphi_1$是两波源的相位差
　　 　　$r_2-r_1$是指定点与两波源的距离之差（波程差$\delta$ ）

　　$\Delta \varphi=\left\{ \begin{array}{ll} 2k\pi &k=0,\pm1,\pm2,\ldots&\text{干涉相长} \\ (2k+1)\pi &k=0,\pm1,\pm2,\ldots & \text{干涉相消}\end{array}
\right.$

　　2）当$\varphi_2=\varphi_1$时，判断条件可用波程差表示为：

　　$\delta =\left\{ \begin{array}{ll} k\lambda &k=0,\pm1,\pm2,\ldots&\text{干涉相长} \\ (2k+1)\cfrac \lambda 2 &k=0,\pm1,\pm2,\ldots & \text{干涉相消}\end{array}
\right.$

下一章“光的干涉”的理论基础

四、驻波

1. 驻波

　　振幅、频率相同的两列相干波，在同一直线上沿相反方向传播时叠加形成的一种特殊的干涉现象.

2. 驻波方程

　　沿$x$正向传播的$y_1=A\cos(\omega t-\cfrac {2\pi} \lambda x)$ 和沿$x$轴负向传播的$y_2=A\cos(\omega t+\cfrac {2\pi} \lambda x)$叠加后，形成驻波，其驻波方程为:
　　$y=y_1+y_2=2A\cos2\pi\cfrac x \lambda\cos\omega t$

备注: 1）驻波方程需依据实际的正向、反向波函数叠加确定，以上方程仅是特例。
　　2）叠加运算时用三角函数和差化积公式：
$\cos \alpha+\cos \beta=2\cos \cfrac {\alpha +\beta} 2 \cos\cfrac {\alpha - \beta} 2$

3. 驻波的特征

　　具有波节、波腹，相邻波节(波腹)距离$\cfrac \lambda 2$
　　按驻波方程中坐标$x$所在$\cos$函数讨论波节、波腹的位置。

五. 声波

　　声波的频率范围
　　声强 $I=\cfrac 1 2\rho A^2 \omega^2$
　　声强级 $L=\lg \cfrac I {I_0}$

六. 多普勒效应

（1）现象

　　当波源和观察者之间有相对运动时，接收频率将与发射频率不等。
　　相互接近时,接收到的频率高于波源频率。
　　只有波源和观察者相对静止时，接收频率和发射频率才相等。

（2）频率关系　 $\nu ' =\cfrac {u\pm\nu_o}{u\mp \nu_s}\nu$

　　$\nu$ ：发射频率－ 波源振动的频率
　　$\nu'$：接收频率 － 单位时间内观测者接收到的振动次数或完整波数.
　　$u$ ：波速， $\nu_o$：观察者速率，$\nu_s$ ：波源速率

　　$\nu_o$前符号: 观察者向波源运动取“＋”，远离取“－”
　　$\nu_s$前符号: 波源向观察者运动取“－”，远离取“＋”

备注：对方接近时，取上栏符号，向对方远离时，取下栏符号。判断“接近”/“远离”时，假定对方未动

或：与$u$同方向时，取“－”号，与$u$反方向时，取“＋”号，如下图）