fmingde
版次: 2024
了解本系列其他文章，请浏览目录：
《大学物理》内容提要目录

§7 恒定磁场

一、理论基础：毕奥-萨伐尔定律

1. 毕奥-萨伐尔定律 $\vec B= \cfrac {\mu_0} {4\pi }\int_l \cfrac {I{\rm d}\vec l\times \vec e_r}{r^2}$

　　$\mu_0=4\pi\times 10^{-7}\;\rm N\cdot A^{-2}$为真空中磁导率
　　电流元$I{\rm d}\vec l$在位置 $\vec r$产生${\rm d}\vec B$ : $d\vec B =\cfrac {\mu_0} {4\pi } \cfrac {I{\rm d}\vec l\times \vec e_r}{r^2}$，整段电流在位置$\vec r$ 产生$\vec B$ : $\vec B=\int_l {\rm d}\vec B$ 。

2. 常用结论

（1）载流直导线的磁感强度

1）有限长载流直导线的磁感应强度
　　
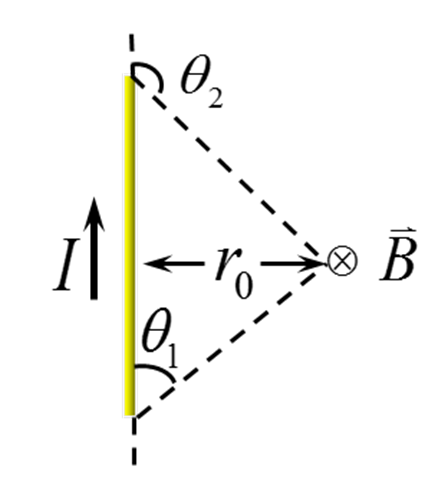
　　$B=\cfrac {\mu_0I} {4\pi r_0} (\cos\theta_1-\cos\theta_2)$

2）无限长载流直导线的磁感强度 $B=\cfrac {\mu_0 I} {2\pi r_0}$

另: 半无限长直导线端面上 $B=\cfrac {\mu_0 I} {4\pi r_0}$

（2）圆形载流导线圆心处磁感强度 $B=\cfrac {\mu_0 I} {2 R}$

（3）直螺线管内部 $B=\mu_0nI$

另：直螺线管端面 $B=\cfrac 1 2 \mu_0nI$

计算要求：★★★ 由以上常用结论，用叠加原理、微元法计算磁感强度
典型习题：三、2，3

3. 拓展：运动电荷的磁场

　　运动中的电荷，可等效为电流或电流元后，按恒定电流估计其磁场

（1）运动电荷在空间产生的磁场，形式上与毕奥-萨伐尔定律相似 $\vec B=\cfrac {\mu_0} {4\pi} \cfrac {q\vec v \times \vec e_r}{r^2}$

（2）圆周运动的电荷或转动的带电圆环，可等效为环形电流$I=\cfrac q T$ ，$T$是圆周运动周期

二、磁场的性质

0. （曲面$S$上的）磁通量　$\it \Phi_m=\int_S \vec B\cdot {\rm d} \vec S$　

计算要求：磁通量的定义、计算。磁通量的计算，常融合在下一章电磁感应相关计算中。
典型习题：三、6

1. 磁场高斯定理　 $\it \Phi_m= \oint_S \vec B\cdot {\rm d} \vec S=0$

　磁感应强度矢量在闭合曲面上的通量为零
　　磁场高斯定理说明：磁场是无源场

2. 安培环路定理 　　$\oint_l \vec B\cdot {\rm d} \vec l=\mu_0\sum \limits_{i=1}^n I_i$

　　磁感应强度矢量在闭合路径$l$上的环流，等于路径所包围电流代数和的$\mu_0$倍
　　磁场的安培环路定理表明：磁场是涡旋场

计算要求：★★★用安培环路定理计算具备对称性的磁场的磁感强度
典型习题：三、 4,5,6

三、磁场对电荷、电流的作用

1. 对运动电荷的作用：沦仑兹力 $\vec F_m=q\vec v\times \vec B$

　　推广：带电粒子在电场和磁场中的受力

　　$\vec F=q\vec E+q\vec v\times \vec B$

　　示例1：运动电荷在均匀磁场中作螺线运动，其回旋半径、回旋周期、螺距为:

　　$R=\cfrac {mv_{\bot}} {qB}$ ，$T=\cfrac {2\pi R}{v_{\bot}}=\cfrac {2\pi m}{qB}$ ，$h=\cfrac {2\pi m}{qB}v_{\scriptscriptstyle //}$

　　示例2：霍尔效应：磁场中，导体中载流子受到洛伦兹力，向导体侧面累积，形成电势差。
　　霍尔电势差: $U_H=R_H\cfrac {BI}d=\cfrac 1 {nq}\cfrac {BI} d$

　　霍尔效应可用于实验判定半导体类型。
　　N型半导体，载流子是电子（负电荷）
　　P型半导体，载流子是“空穴”（正电荷）
　　同一场景，采用$P$ 型半导体或$N$型半导体时，霍尔电势差符号相异。电势高低，需根据载流子受力、累积方位来确定。

2. 对电流的作用力：安培力　$\vec F=\int_lI{\rm d}\vec l\times \vec B$

　　安培定律：电流元在磁场中受力为：${\rm d}\vec F=I{\rm d}\vec l\times \vec B$，整段电流，受力为：$\vec F=\int_l{\rm d}\vec F$

　　均匀磁场中的结论：
　　1）任意空间载流导线在均匀磁场中所受的力，与其在垂直磁场平面上的“投影导线”所受的磁场力相同；2）任意(垂直于磁场的)平面载流导线在均匀磁场中所受的力，与其始点和终点相同的载流直导线所受的磁场力相同；3）安培力的功，可用$W=IB\Delta S$ 快速计算， $\Delta S$是导线“横扫”过的面积。

计算要求：★★ 载流导线在磁场中的受力计算
典型习题：三、7,8

3. 对载流线圈的作用：磁力矩 　$\vec M=\vec m\times\vec B$

　　
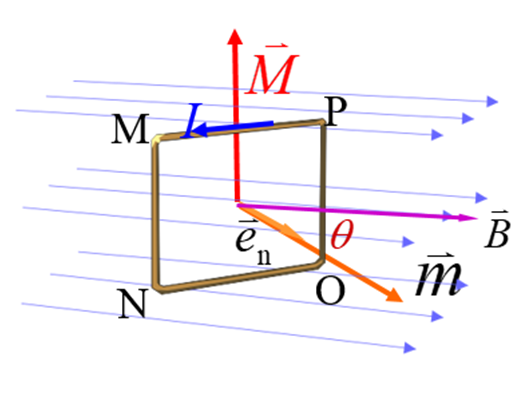
　　$\vec m$ ：线圈的磁矩，是（通电）线圈自身属性：$\vec m=NIS\vec e_n$；$N$：线圈的圈数（匝数)，$S$：线圈的面积，按电流$I$ 绕向，按右手螺旋定则，确定线圈法向$\vec e_n$。

　　磁力矩试图使线圈的磁通量最大化。
　　磁力矩做功：$W=\int_{\theta_1}^{\theta_2}-M{\rm d}\theta$

备注：刚体力学中： $W=\int_{\theta_1}^{\theta_2}M{\rm d}\theta$，$\theta$ 是转动角坐标。与磁力矩大小$M=ISB\sin\theta$中 $\theta$含义不同。采用后者来表达的话， $W=\int_{\theta_1}^{\theta_2}-M{\rm d}\theta$
例: 由力矩最大位置转到力矩为零位置，磁力矩的功为： $W=\displaystyle \int_{\frac \pi 2}^{0}-ISB\sin \theta \,{\rm d}\theta=ISB=I\Delta \it \Phi$，为正功

　　磁力矩做功，可表达为$W=I\Delta \it \Phi$ ， $\Delta \it \Phi$是磁通量增量

计算要求：★ 载流线圈在磁场中的力矩计算

典型习题：三、8, 9

四、磁介质

1. 磁介质的种类

　　1）顺磁质：$\mu_r>1$ ，增强原磁场；2）抗磁质：$\mu_r<1$ ，增强原磁场；3）铁磁质：$\mu_r>>1$ ，大大增强原磁场

2. 磁介质的磁化

　　顺磁质固有磁矩的取向磁化或抗磁质附加磁矩的产生都使磁介质表面（或内部）出现磁化电流。
　　磁化强度矢量：$\vec M=\cfrac {\sum \vec m}{\Delta V}$

　　磁化电流密度：$\vec j'=\vec M\times \vec n$

3. 磁介质中的安培环路定理

（1）磁场强度 $\vec H$
一般情况 $\vec H=\cfrac {\vec B} {\mu_0}-\vec M$
在线性各向同性介质中 $\vec H=\cfrac {\vec B}{\mu}$

　　即 $\vec B=\mu\vec H=\mu_0\mu_r\vec H$

（2）介质中安培环路定理： $\displaystyle \oint _l\vec H\cdot {\rm d}\vec l=\sum \limits_{\text{内}}I$

计算要求：★★ 含介质时，对称磁场的计算
典型习题：三、10

§8 电磁感应 电磁场

〇、物理量准备：电流、电流密度、电动势

1. 电流(强度)$I$ : 单位时间内通过导体横截面的电量　$I=\cfrac {{\rm d}q} {dt}$

2. 电流密度(矢量)　 $\vec j$

　　大小:单位时间内过(垂直于正电荷运动方向的)单位面积的电荷,
　　方向: 该点正电荷运动方向

3. 电流密度与电流的关系

　　电流强度是电流密度矢量的“通量” ：$I=\displaystyle \int_S \vec j\cdot {\rm d}\vec S$

4. 电源

　　逆电势方向“搬运”电荷的装置，将其他形式能量转换为电势能的装置。

　　电源内，靠“非静电力” $\vec F_k$ “搬运”电荷。

　　称$\vec E_k=\cfrac {\vec F_k}{q}$为“非静电力”场强。

5. 电动势　$\mathscr E= \int_-^+\vec E_k\cdot{\rm d}\vec l$

　　衡量电源转换能量大小的物理量，反映了电源中非静电力做功的本领
　　

　　数值等于将单位正电荷自负极移到正极时，非静电力所做的功

6.电动势的方向

　　由负极经内电路指向正极, $\vec E_k$ 的方向

一、理论基础：法拉第电磁感应定律

1. 法拉第电磁感应定律 　$\mathscr E_i=-\cfrac {{\rm d}\it \Phi_m}{{\rm d}t}$

2. 楞次定律

　　闭合回路中感应电流的方向，总是使得它所激发的磁场在回路中的磁通量,阻碍（引起感应电流的）磁通量的变化。

计算要求：★★★ 计算(闭合导线)感应电动势、感应电流
典型习题：三、1,2,3,6

二、动生电动势和感生电动势

1. 动生电动势

　　磁场分布不随时间变化，导线在磁场中“切割”磁力线时的电动势

　　非静电力: 沦仑兹力

　　计算式: $\mathscr E_i= \int_l (\vec v\times\vec B)\cdot{\rm d}\vec l$

2. 感生电动势

　　磁场随时间变化，产生感生电场。感生电场在路径上形成的电动势

　　非静电力: 感生电场的电场力

　　计算式: $\mathscr E_i=\displaystyle \int_l \vec E_k\cdot{\rm d}\vec l$ 　　$\vec E_k$为感生电场场强

计算要求：★★ 计算(分段导线上)感应电动势

典型习题：三、4,5

三、感生电场

　　变化的磁场产生涡旋的感生电场。
　　

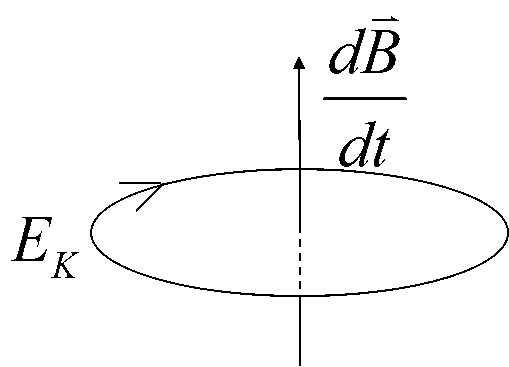
　　$\oint_l\vec E_k\cdot{\rm d}\vec l=-\int_S \cfrac {\partial \vec B}{\partial t}\cdot {\rm d}\vec S$
　　（上式直接来源于法拉第电磁感应定律）
　　可用于柱对称感生电场的计算。
　　

　　例如: 当圆柱空间内磁场均匀，变化率为$\frac {{\rm d}B}{{\rm d}t}$时，选同心圆环为积分路径，则有
　　$E_k\cdot2\pi r=\cfrac {{\rm d}B}{{\rm d}t}\cdot \pi r^2$

计算要求：★柱对称分布感生电场的计算

四、自感电动势和互感电动势

1. 自感电动势

　　$\mathscr E_L=-L\cfrac {{\rm d}I}{{\rm d}t}$

2. 自感系数的计算

　　假设电流为$I$，计算其产生的磁通量$\it \Phi$ ，则：$L=\cfrac {\it \Phi} {I}$

　　（$L$与线圈实际有无电流无关）

3. 互感电动势

　　$\mathscr E_{12}=-M\cfrac {{\rm d}I_2}{{\rm d}t}$

　　$\mathscr E_{12}$为线圈2中电流$I_2$变化在线圈1中产生的电动势

4. 互感系数的计算

　　假设线圈1中电流为$I$，计算其在线圈2中产生的${\it \Phi}_{21}$，则$M=\cfrac {{\it \Phi}_{21}} {I_1}$

　　（$M$与线圈1，2中，实际有无电流无关）

计算要求：★自感系数的计算
　　　　　★互感系数的计算
典型习题：三、8

五、磁场的能量

1. 自感线圈的能量　$W_m=\cfrac 1 2LI^2$

2. 磁场的能量密度　$w_m=\cfrac 1 2 \cfrac {B^2} \mu$

3. 磁场的能量　$W_m= \int_Vw_m{\rm d}V$

备注：磁场储能的计算方法: 1）若已计算$B$，可用空间积分求和，计算磁场。2）若已计算自感系数$L$ ，按$W_m=\frac 1 2LI^2$计算储能。

计算要求：★磁场储能计算

六、电场和磁场的联系

1. 变化的磁场产生电场: 感生电场

　　$\oint_l\vec E_k\cdot{\rm d}\vec l=-\int_S \cfrac {\partial \vec B}{\partial t}\cdot {\rm d}\vec S$

2. 变化的电场产生磁场: 位移电流

　　$I_d=\cfrac {{\rm d}\it \Psi}{{\rm d}t}$ 　　$\vec j_d=\cfrac {\partial \vec D}{\partial t}$

　　麦克斯韦电磁理论的两条基本假设之二：变化的电场，能等效为位移电流，产生磁场。

　　包含位移电流的安培环路定理：
　　$\oint_l \vec H \cdot{\rm d}\vec l=\int_S(\vec j_d+\cfrac {\partial \vec D}{\partial t})\cdot {\rm d}\vec S$

3. 电磁场的基本方程

　　$\oint_S \vec D \cdot{\rm d}\vec S=\int_V\rho{\rm d}V=q$ 　　　自由电荷产生发散的电场。

　　$\oint_l\vec E_k\cdot{\rm d}\vec l=-\int_S \cfrac {\partial \vec B}{\partial t}\cdot {\rm d}\vec S$　　　变化磁场产生涡旋的电场。

　　$\oint_S \vec B \cdot{\rm d}\vec S=0$　　　　　　　　　磁场不发散。

　　$\oint_l \vec H \cdot{\rm d}\vec l=\int_S(\vec j_d+\cfrac {\partial \vec D}{\partial t})\cdot {\rm d}\vec S$　传导电流和变化电场产生涡旋的磁场。