fmingde
版次: 2024-2
了解本系列其他文章，请浏览目录：
《大学物理》内容提要目录

§1 质点运动学

一、描述质点运动的物理量(线量)

1. 位置矢量 　$\vec r$

　　1）由参考点指向质点位置的矢量；2）位置矢量随时间的变化关系，称为运动方程$\vec r(t)$；3）运动方程完整的描述了质点运动，由运动方程可导出其他描述质点运动的物理量、表达式。

2. 位移矢量　$\Delta \vec r = \vec r _2 - \vec r _1$

　　反映位置变化(方位及距离)

3. (瞬时)速度矢量　 $\vec v = \cfrac{{\rm d}\vec r} {{\rm d}t}$

　　1）是平均速度($\overline{\vec v} = \cfrac{\Delta \vec r} {\Delta t}$)的极限；2）是位置矢量对时间的变化率；3）反映质点空间位置变化的快慢和方向。

4. (瞬时)加速度矢量　$\vec a = \cfrac{{\rm d} \vec v} {{\rm d}t}$

　　1）是平均加速度($\overline{\vec a} = \cfrac{\Delta \vec v} {\Delta t}$)的极限；2）是速度矢量对时间的变化率；3）反映速度对时间的变化快慢和方向。

5. 小结: 位置矢量、速度矢量、加速度矢量的联系

（1）后者是前者的“变化率”
　　$\vec r(t) \xrightarrow[]{\,\quad\frac {{\rm d} \vec r}{{\rm d}t}=\vec v \quad} \vec v(t) \xrightarrow[]{\,\quad \frac {{\rm d} \vec v}{{\rm d}t}=\vec a \quad} \vec a(t)$

（2）前者是后者的“累积”
　　$\vec r(t) \xleftarrow[\vec r=\vec r_0+\int^t_{t_0} \vec v{\rm d}t]{} \vec v(t) \xleftarrow[\vec v=\vec v_0+\int^t_{t_0} \vec a{\rm d}t]{} \vec a(t)$

（3）备注：由导数式$\vec v=\cfrac {{\rm d} \vec r}{{\rm d}t}$，转化为积分式的过程：
　　$\vec v=\cfrac {{\rm d} \vec r}{{\rm d}t} \xrightarrow[]{\text{移项}}\vec v{\rm d}t={\rm d}\vec r\xrightarrow[\text{上下限对应}]{\text{两边定积分}}\int^t_{t_0}\vec v{\rm d}t=\int^{\vec r}_{\vec r_0}{\rm d}\vec r$
　　$\vec v$对$t$积分，得到的是位置矢量增量（即位移）$\Delta\vec r=\vec r-\vec r_0$ ，类似地，　$\vec a$对$t$积分，得到的是$\vec v$的增量$\Delta \vec v=\vec v_2-\vec v_1$

计算要求：★★已知运动方程，1）求速度加速度、轨迹等 2）判断运动特点
典型习题：三、1

计算要求：★★★已知加速度或速度， 并辅以初始条件，求运动方程
典型习题：三、3

6. 备注：直角坐标系下各量、各关系的分解形式

　　$\vec r=x \vec i+y \vec j+z \vec k$ 　　 $\Delta \vec r=\Delta x \vec i+\Delta y \vec j+ \Delta z \vec k$

　　$\vec v=v_x \vec i+v_y \vec j+v_z \vec k$

　　$\vec a=a_x \vec i+a_y \vec j+a_z \vec k$

　　$\vec v= \cfrac {{\rm d} \vec r} {{\rm d}t} =\cfrac {{\rm d} x} {{\rm d}t} \vec i+\cfrac {{\rm d} y} {{\rm d}t} \vec j+\cfrac {{\rm d} z} {{\rm d}t} \vec k$

　　$\vec a= \cfrac {{\rm d} \vec v} {{\rm d}t} = \cfrac {{\rm d}^2 \vec r} {{\rm d}t^2}=\cfrac {{\rm d}^2 x} {{\rm d}t^2} \vec i+\cfrac {{\rm d}^2 y} {{\rm d}t^2} \vec j+\cfrac {{\rm d}^2 z} {{\rm d}t^2} \vec k$

7. 备注：微分式到积分式的变换过程

（1）由微分式进行积分
　　将导数式，整理为微分等式，两边加积分号。
　　为了使两边的积分可展开，需“分离变量”，将与被积变量相关的项移到被积变量同侧。
　　例：$v=kx$ $\xrightarrow[]{\text{$v$展开}} \quad \cfrac {{\rm d}x}{{\rm d}t}=kx$ $\xrightarrow[]{\text{分离变量}} \quad\cfrac 1 x {\rm d}x=k{\rm d}t$
　　$\xrightarrow[]{\text{两边加积分号}} \quad\int^{x_2}_{x_1} \cfrac 1 x {\rm d}x=\int^{t_2}_{t_1}k{\rm d}t$

（2） 变上限积分 将定积分上限指定为变量本身，得到变量间的函数关系
　　例：$v=kx$ $\xrightarrow[]{\text{改写成积分}} \quad\int^{x}_{x_0} \cfrac 1 x {\rm d}x=\int^{t}_{t_0}k{\rm d}t$
　　 $\xrightarrow[]{} \quad \ln x - \ln x_0 =k(t-t_0)$ $\xrightarrow[]{} \quad x=x_0e^{k(t-t_0)}$

（3）变换被积变量
　　某些问题中，需要将对时间的积分，变成对位置量（坐标、角度等）的积分。
　　1）变换方法：尝试在导数式的上下部分同时“乘以”中间变量的微分。
　　例: $\cfrac {{\rm d}v}{{\rm d}t}=\cfrac {{\rm d}v}{{\rm d}t} \cfrac {{\rm d}\theta}{{\rm d}\theta}=\omega\cfrac {{\rm d}v}{{\rm d}\theta}$，然后移项、积分。
　　2）典型应用：
　　圆周运动 －乘以角坐标的微分(如:${\rm d}\theta$)
　　直线运动(分运动) －乘以坐标的微分(如:${\rm d}x$)
　　曲线运动 －乘以路程的微分(如: ${\rm d}s$)

8. 注意：矢量符号、标量符号的意义

　　以速度矢量$\vec v$为例:

　　$v$：速度矢量的大小，$v= \vert {\vec v} \vert$ ，与速率相同

　　$\Delta \vec v$ ：速度矢量的增量$\Delta \vec v= \vec v_2-\vec v_1$

　　$\vert\Delta \vec v \vert$：速度矢量增量的大小$\vert \Delta\vec v \vert=\vert \vec v_2-\vec v_1\vert$

　　$\Delta v$ ：速率的增量，$\Delta v=v_2-v_1=\vert \vec v_2\vert-\vert \vec v_1 \vert$

9. 注意：路程等相关概念

　　路程：$\Delta S$ ，（$\Delta t$时间内）运动轨迹的长度

用了增量符号$\Delta$，可理解为：$\Delta S=S_2-S_1$，$S$是自计时起点起，运动轨迹的长度值。

　　平均速率： $\overline v=\cfrac {\Delta S}{\Delta t}$

　　瞬时速率：$v= \cfrac {{\rm d}S} {{\rm d}t}$ , 平均速率的极限
　　因${\rm d}S=\vert {\rm d} \vec r \vert$ ，瞬时速率即为瞬时速度矢量的大小。(故速率的符号为$v$，$v=\vert \vec v\vert$ )

二、加速度(按自然坐标系)的分解

1. 自然坐标系
　　

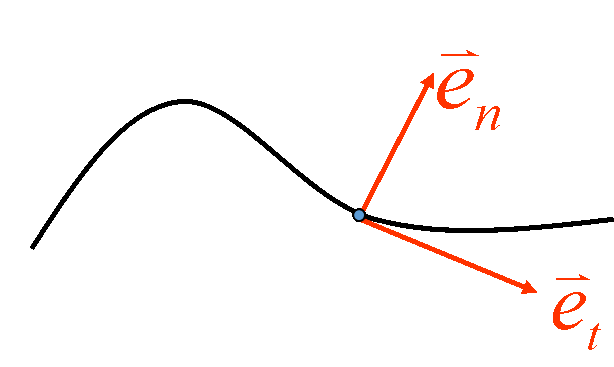
　　切向，沿质点前进方向为正，单位矢量$\vec e _t$
　　法向，轨迹凹侧为正，单位矢量$\vec e_n$

自然坐标系主要用于力、加速度等的分解。

2. 加速度的分解，切向加速度和法向加速度

　　加速度，可按自然坐标系，分解为切向加速度和法向加速度。
　　$\vec a=a_t\vec e_t+a_n\vec e_n$

　　$a_t=\cfrac {{\rm d}v} {{\rm d}t}$ 切向加速度 — 反映速度大小的变化
　　$a_n= \cfrac {v^2} \rho$法向加速度 — 反映速度方向的变化

三、(圆周)运动的角量描述

1. 角坐标、角位置　$\theta$

　　角坐标随时间的变化关系$\theta(t)$，称为角量运动方程。

2. 角速度　$\omega= \cfrac {{\rm d}\theta} {{\rm d}t}$

3. 角加速度　$\alpha=\cfrac {{\rm d}\omega}{{\rm d}t}$　

4. 小结: 角坐标、角速度、角加速度的联系

（1）后者是前者的“变化率”
　　$\theta(t) \xrightarrow[]{\,\quad\frac {{\rm d} \theta}{{\rm d}t}=\omega \quad} \omega(t) \xrightarrow[]{\,\quad \frac {{\rm d} \omega}{{\rm d}t}=\alpha \quad} \alpha(t)$

（2）前者是后者的“累积”
　　$\theta(t) \xleftarrow[\theta=\theta_0+\int^t_{t_0} \omega {\rm d}t]{} \omega(t) \xleftarrow[\omega =\omega_0+\int^t_{t_0} \alpha {\rm d}t]{} \alpha(t)$

5. 与线量的联系

　　对距圆心$r$处的点：

　　速率：$v=r\omega$

　　加速度分量: $\begin{cases} a_t=r\alpha \ a_n =r\omega^2\end{cases}$

计算要求：★已知角量运动方程，1）求角速度、加速度 2）求相应的线 速度、法向加速度、切向加速度
典型习题：三、4

四、(伽利略)速度变换式, 运动的相对性

1. (伽利略)速度变换式　$\vec v =\vec v'+\vec u$

　　$\vec v$ ：质点相对基本参考系$S$的速度，${\vec v}'$ ：质点相对运动参考系$S’$的速度记为(相对速度)，$\vec u$：运动参考系$S’$相对基本参考系$S$的速度。

　　推广形式：$\vec v_{AB}=\vec v_{AC} +\vec v_{CB}$，$A$相对于$B$的速度，等于$A$相对于$C$的速度与$C$相对于$B$的速度的矢量和。

计算要求：★运用速度变换，求相对速度。 常融合在其他力学问题中。
典型习题：三、6

§2 牛顿定律

一、牛顿三大运动定律

1. 牛顿第一定律

　　任何物体都保持静止或匀速直线运动的状态，直至其它物体对它作用的力迫使它改变这种状态。
　　牛顿第一定律指出物体具有惯性，并定义了惯性参考系：符合第一定律的参考系，称为惯性参考系。

2. 牛顿第二定律　$\vec F=m\vec a$

　　揭示了力是引起运动状态改变的原因
（1）原始形式 $\vec F=\cfrac {{\rm d} \vec p}{{\rm d}t}$
　　因（经典力学中）质量是常数， $\vec F=\cfrac {{\rm d} \vec p}{{\rm d}t}=m\cfrac {{\rm d}\vec v} {{\rm d}t}=m\vec a$

（2）在直角坐标系下:$\vec F=ma_x\vec i+ma_y \vec j+ma_z\vec k$
　　分量式为 $\begin{cases} F_x=ma_x \ F_y=ma_y \ F_z=ma_z \end{cases}$

（3）在自然坐标系下:$\vec F=m(\vec a_t+\vec a_n)=m\cfrac {{\rm d}v}{{\rm d}t}\vec e_t+m\cfrac {v^2}{\rho} \vec e_n$
　　分量式为$\begin{cases} F_t=ma_t=m \cfrac {{\rm d}v}{{\rm d}t} \ F_n=ma_n=m\cfrac{v^2}{\rho} \end{cases}$

3. 牛顿第三定律

　　两个物体之间的作用力和反作用力沿同一直线，大小相等，方向相反，分别作用在两个物体上。$\vec F=-\vec F'$

二、牛顿定律应用

1. 常见的三类力

　　1）万有引力(重力)；2）弹性力(压力、支持力、拉力、弹簧弹力) ；3）摩擦力(静摩擦力、滑动摩檫力)

2. 牛顿定律的应用

（1） 确定研究对象：质点或质点组合
（2）单个质点的受力分析
　　质点在力场中，存在场力，如重力、静电力
　　与其他物体相互接触，可能存在弹性力，如压力、支持力、拉力、弹簧弹力
　　与其他物体接触，并有相对运动，或有相对运动趋势，存在摩擦力

（3）运动状态分析
　　各质点的牛顿第二定律分量式
　　质点之间的牵连关系

计算要求： ★★一般运动中，牛顿第二定律的应用 多个牵连物体(如滑轮悬挂)， 需对各物体应用牛顿第二定律，联立方程组求解
典型习题：三、1,2

计算要求：★★圆周运动中牛顿第二定律的应用 需要法向加速度以及法向(向心)力
典型习题：三、3

§3 动量守恒定律和能量守恒定律

一、动量定理、动量守恒定律 － 力对时间的累计效应

1. 质点的动量定理 　$\int^{t_2}_{t_1}\vec F{\rm d}t=\vec p_2-\vec p_1$

　　1）力对时间的累积 → 动量的增量 ；2）$\vec I=\int^{t_2}_{t_1}\vec F{\rm d}t$ 称为“冲量”；3）$\vec p=m\vec v$, 质点的动量

2. 质点系的动量定理　 $\int^{t_2}_{t_1}\vec F^{ex}{\rm d}t=\vec p_2-\vec p_1$

　　1）合外力对时间的累积 → 系统动量的增量；2）描述的是两个及以上的质点组成的质点系统，需区分内力（$\vec F^{in}$）、外力（$\vec F^{ex}$）。3）内力对系统的动量改变无贡献（成对内力的合冲量为零）

3. （质点系的）动量守恒定律

　　1）若$\vec F^{ex}=0$，$\vec p=$恒矢量；2）在直角坐标系中，若某一坐标轴方向外力为零，则“该方向的动量守恒”。（总动量不一定守恒）
　　如: 若$F_x=0$, $p_x=$恒量。

计算要求：★★动量定理应用。 1）冲量的直接计算(力对时间积分)和间接计算(动量的增量) 2）确定末运动状态 3）计算平均冲力
典型习题：一、1，2

计算要求：★★★由动量守恒定律应用。 1）碰撞问题 2）某一方向上的动量守恒
典型习题： 一、3

二、动能定理 － 力对空间的累计效应

1. 功　 $W= \int^b_a \vec F \cdot {\rm d}\vec r$
　　

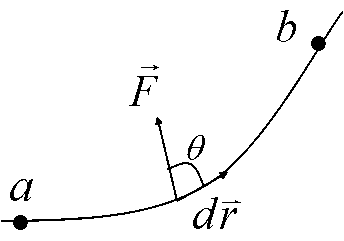
　　力对物体所做的元功等于力在物体位移方向的分量（切向力）与元位移大小的乘积，总功是过程中元功的数量和。

　　1）${\rm d}W=\vec F \cdot {\rm d}\vec r$　　$W= \int^b_a \vec F \cdot {\rm d}\vec r$；　2）分解式 $W=\int^{x_b}_{x_a}F_x{\rm d}x+\int^{y_b}_{y_a}F_y{\rm d}y+\int^{z_b}_{z_a}F_z{\rm d}z$；3）对恒力，简化为： $W=\vec F \cdot \Delta \vec r$

2. 动能　$E_k=\cfrac 1 2 mv^2$、质点的动能定理　$W=E_{k2}-E_{k1}$

　　简单表示为$W=\Delta E_k$, 功等于质点动能的增量

3. 质点系的动能定理　$W^{ex}+W^{in}=E_{k2}-E_{k1}$

　　所有力（内力、外力）的功等于系统动能的增量

　　成对内力所作的总功不一定为零。是否做功取决于两受力物体有无相对位移。

计算要求：★★动能定理的应用。 1）功的直接计算（力对时间积分）和间接计算（动能增量） 2）确定末运动状态
典型习题：一、4, 5

三、（物体系）的势能

1. 保守力

　　做功只由起点、终点位置决定的力

　　保守力做功与路径无关

2. 势能　$E_p$

　　对保守力，可定义对应的势能。保守力在两位置间做的功，等于该势能在两位置间的减少量（增量的负值）。 $W=-\Delta E_p$

　　势能是相对的，指定势能零点后，才能确定各位置的势能取值。

　　势能属于产生保守力相互作用的系统，引用势能时，隐含选择了以系统为研究对象。

3. 常见势能

（1）重力势能$E_p=mgh$
　　$h$为相对势能零点平面的高度。重力势能属于物体和地球组成的系统。

（2）弹簧的弹性势能$E_p= \cfrac 1 2kx^2$
　　$x$为弹簧的伸长量。弹簧的弹性势能属于弹簧和物体组成的系统。

计算要求：势能的计算，常融合在功能原理、机械能守恒定律等问题中

四、功能原理和机械能守恒

1. 机械能　$E=E_k+E_p$

　　系统动能和势能的总和

2. 功能原理　$W^{ex}+W_{nc}^{in}=E_2-E_1$

　　外力和非保守内力的功，等于系统机械能的增量

　　对保守力引入势能后，保守力作的功可用势能的变化代替。故质点系的动能定理，可变化为用机械能表达。 　　

2. 机械能守恒　若$W^{ex}+W_{nc}^{in}=0$, $E=$恒量

　　只有保守力（重力、弹力等）做功时，可适当选择系统，使保守力成为内力。此时，系统的机械能守恒。

计算要求：★★★机械能守恒定律的运用
典型习题：三、6

五、质心，质心运动定律

1. 质心　 $\vec r_c= \cfrac 1 M \int \vec r {\rm d}m$

　　其中$M=\int {\rm d}m$ ,为质点系总质量
　　1）质心是质点系质量分布的平均位置；2）分量式: $x_c= \cfrac 1 M \int x{\rm d}m$ $y_c= \cfrac 1 M \int y{\rm d}m$ $z_c= \cfrac 1 M \int z{\rm d}m$ ； 3）对密度均匀、形状对称的物体，质心在其几何中心．

2. 质心运动定律　$\vec F^{ex} = M\vec a_c$

　　作用在系统上的合外力等于系统的总质量与系统质心加速度的乘积。

计算要求：质心的计算
典型习题：三、7