PeiLingX
物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》第28课。
了解本系列及本专栏其他文章,请收藏目录:
0) 开篇语
上节课我们导出了狄拉克方程,并且由方程解的性质导出了概率流密度(虽然我们还没正式求解方程),由此看到,狄拉克方程解决了K-G方程的第一个问题:负概率问题。
这节课,我们要来正式求解最简单情形下的狄拉克方程,看看它还能给我们带来哪些已知的和未知的物理事实,特别是我们一直提到的自旋将以怎样的方式从狄拉克方程中出现。
注:本文中出现的算符有时候会加上hat、有时候又忘了加,而三个方向的脚下标有时候用的是$x,y,z$、有时候又用的是1,2,3,相信这不会影响阅读和理解,以后再慢慢整理和规范化吧……
1) 自由粒子解
我们在推导狄拉克方程的时候,暂时没考虑势能项,这就意味着,我们前面给出的狄拉克方程是描述自由粒子的(今后会讨论有势能情形下的方程形式),这方便我们快速求解,并且足够让我们从解中发现一些有意思的物理意义。
现在,我们先把解算出来。
推导过程作者是根据自己作为普通人的智商水平为标准来写的,因此可能会显得有点啰嗦甚至笨拙,如果同学们遇到一些看起来很显然而没有必要写出来的步骤,可以直接跳过。
由于方程是线性的,且对时间和空间的导数都是一阶,所以我们不妨假设解是一个包含了时间和空间变量的线性函数的复指数(下式中红色部分,这是一阶线性常系数微分方程解的通用形式)乘以一个四分量旋量(下式中蓝色部分)的形式:
$\small \boldsymbol \psi=\begin{bmatrix}\psi_1\\ \psi_2\\ \psi_3\\ \psi_4\end{bmatrix}=\color{blue}{\begin{bmatrix}\phi^{(L)}\\ \phi^{(R)}\\ \chi^{(L)}\\ \chi^{(R)}\end{bmatrix}}\color{red}{\exp{\left[\frac{\text i}{\hbar}\left(Et-p_xx-p_yy-p_zz\right)\right]}} \quad{\scriptsize(式28.1)}$
其中$ \small \phi^{(L)},\ \phi^{(R)},\ \chi^{(L)},\ \chi^{(R)} $的含义以后会解释(相信同学们能看出上标L, R分别代表Left和Right……)。
对$ \small \boldsymbol \psi $求$ \small t,x,y,z $的偏导数,就能分别得到$ \small E,p_x,p_y,p_z $的本征值,再约去两边的复指数,方程就变成了:
$\small \begin{align} E\begin{bmatrix}\psi_1\\\psi_2\\\psi_3\\\psi_4\end{bmatrix}=\begin{bmatrix}mc^2&0&p_3c&p_1c-\text ip_2c\\0&mc^2&p_1c+\text ip_2c&-p_3c\\p_3c&p_1c-\text ip_2c&-mc^2&0\\p_1c+\text ip_2c&-p_3c&0&-mc^2\end{bmatrix}\begin{bmatrix}\psi_1\\\psi_2\\\psi_3\\\psi_4\end{bmatrix} \end{align} \quad{\scriptsize(式28.2)}$
这就回到了一个明显的4×4矩阵的本征方程形式,它的本征值正好就是能量本征值,本征态乘以复指数函数就是能量本征态。
我们可以用线性代数中求特征值和特征向量的标准流程来求能量本征值和本征态,或者直接关门放Matlab。
但这里我们不打算这么做,而是要用一种看起来有点绕的方式来计算它们,因为这样可以将本征态表示为方便后面讨论物理意义的形式(而用Matlab直接求解给出来的解的形式不是我们想要的,后面会具体说明)。
首先,将狄拉克方程写成分块矩阵的形式:
$\small \begin{align} E\psi&=\left(\alpha_1\hat p_1c+\alpha_2\hat p_2c+\alpha_3\hat p_3c+\beta mc^2\right)\psi\\ &=\left(\begin{bmatrix}0&\sigma_1\\\sigma_1&0\end{bmatrix}\hat p_1c+\begin{bmatrix}0&\sigma_2\\\sigma_2&0\end{bmatrix}\hat p_2c+\begin{bmatrix}0&\sigma_3\\\sigma_3&0\end{bmatrix}\hat p_3c+\begin{bmatrix}I&0\\0&-I\end{bmatrix}\hat mc^2\right)\psi\\ &=\begin{bmatrix}mc^2&\left(\sigma_1p_1+\sigma_2p_2+\sigma_3p_3\right)c\\\left(\sigma_1p_1+\sigma_2p_2+\sigma_3p_3\right)c&-mc^2\end{bmatrix}\psi\\ \end{align} \quad{\scriptsize (式28.3)}$
令:$ \small \boldsymbol \sigma=(\sigma_1,\sigma_2,\sigma_3) $,则方程可以写为:
$\small \begin{align} E\psi&=\begin{bmatrix}mc^2I&\boldsymbol\sigma \cdot\boldsymbol pc\\\boldsymbol\sigma \cdot\boldsymbol pc&-mc^2I\end{bmatrix}\psi\\ \end{align} \quad{\scriptsize (式28.4)}$
再将方程左右合并:
$\small \begin{align} \begin{bmatrix}\left(E-mc^2\right)I&-\boldsymbol\sigma \cdot\boldsymbol pc\\-\boldsymbol\sigma \cdot\boldsymbol pc&\left(E+mc^2\right)I\end{bmatrix}\psi&=0\ \end{align} \quad{\scriptsize (式28.5)}$
同时将$ \small \psi $也分成上下两块,分别用$ \small \phi $和$ \small \chi $表示:
$\small \begin{align} \begin{bmatrix}\left(E-mc^2\right)I&-\boldsymbol\sigma \cdot\boldsymbol pc\\-\boldsymbol\sigma \cdot\boldsymbol pc&\left(E+mc^2\right)I\end{bmatrix}\begin{bmatrix}\phi\\chi\end{bmatrix}&=0\ \end{align} \quad{\scriptsize (式28.6)}$
注意:$ \small \chi $不是拉丁字母$ \small x $,而是希腊字母chi,读作“凯”
由此可得$ \small \psi $上下两部分的关系:
$\small \left\{\begin{align} \phi=\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E-mc^2}\chi\\ \chi=\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E+mc^2}\phi\\ \end{align} \right. \quad{\scriptsize (式28.7)}$
为了让两个等式自洽,我们不妨将第二个等式代入第一个等式,得到:
$\small \begin{align} \phi&=\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E-mc^2}\chi\\ &=\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E-mc^2}\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E+mc^2}\phi\\ &=\frac{(\boldsymbol\sigma\cdot\boldsymbol p)^2c^2}{E^2-m^2c^4}\phi\ \end{align} \quad{\scriptsize (式28.8)}$
方程要自洽,就意味着上式右边的矩阵要等于2×2的单位矩阵,即:
$\small \begin{align} (\boldsymbol\sigma\cdot\boldsymbol p)^2=\frac{E^2-m^2c^4}{c^2}I\ \end{align} \quad{\scriptsize (式28.9)}$
其中左边等于:
$\small \begin{align} (\boldsymbol\sigma\cdot\boldsymbol p)^2&=\begin{bmatrix}p_3&p_1-\text ip_y\\p_1+\text ip_y&-p_z\end{bmatrix}^2\\ &=\begin{bmatrix}p_3^2+p_1^2+p_2^2&0\\0&p_3^2+p_1^2+p_2^2\end{bmatrix}\\ &=\begin{bmatrix}p^2&0\\0&p^2\end{bmatrix} \end{align} \quad{\scriptsize (式28.10)}$
于是式28.9就可以归为一个方程:
$\small \begin{align} E^2-m^2c^4=p^2c^2\ \end{align} \quad{\scriptsize (式28.11)}$
这样就得到了两个能量本征值解:
$\small E=\pm\sqrt{m^2c^4+p^2c^2} \quad{\scriptsize(式28.12)}$
(没错,狄拉克方程也有负能解,我们后面会看到狄拉克如何解释它)
考虑到式28.2是一个4×4矩阵的特征方程,因此能量本征值有四个,那么一正一负两个解就是两组二重本征值(简并的),即:
$\small \left\{\begin{align} E_1,E_2&=\sqrt{m^2c^4+p^2c^2}\\ E_3,E_4&=-\sqrt{m^2c^4+p^2c^2} \end{align}\right. \quad{\scriptsize(式28.13)}$
这也就意味着,正能解和负能解都各有两组线性无关的本征态,现在我们来找出它们。
如果记:
$\small \begin{align} \frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E+mc^2}=K \end{align} \quad{\scriptsize (式28.14)}$
那么在$ \small E $取两个能量本征值之一的时候,式28.7就可以记为:
$\small \left\{\begin{align} \phi&=K^{-1}\chi\\ \chi&=K\phi\\ \end{align} \right. \quad{\scriptsize (式28.15)}$
两个式子是等价的,我们这里将它们分别写出来,是因为它们代表着不同的自由变量的选取,这有助于我们理解方程解的物理意义。
对于正能解,我们选取$ \small \phi $作为自由变量,那么利用$ \small \chi=K\phi $,就可以将相应的本征态表示为:
$\small \begin{align} u=\begin{bmatrix}\phi\\K\phi\end{bmatrix}=\begin{bmatrix}\phi\\\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E+mc^2}\phi\end{bmatrix} \end{align} \quad{\scriptsize (式28.16)}$
而$ \small \phi $是2×1列向量,并且对应二重能量本征值,因此我们可以任意选取两个基底构造基础解系。
而按照常规做法,不妨就选:
$\small \begin{align} \phi_1=A_1\begin{bmatrix}1\\0\end{bmatrix},\phi_2=A_2\begin{bmatrix}0\\1\end{bmatrix} \end{align} \quad{\scriptsize (式28.17)}$
其中$ \small A_1,A_2 $为归一化系数,为方便推导,后文省略。
则正能解对应的两个特征向量就是:
$\small \begin{align} u_1=\begin{bmatrix}\phi_1\\\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E+mc^2}\phi_1\end{bmatrix}=\begin{bmatrix}1\\0\\\frac{c}{E+mc^2}{\scriptsize\begin{bmatrix}p_3&p_1-\text ip_2\\p_1+\text ip_2&-p_3\end{bmatrix} \begin{bmatrix}1\\0\end{bmatrix}}\end{bmatrix}=\begin{bmatrix}1\\0\\\frac{p_3c}{E+mc^2}\\\frac{p_1c+\text ip_2c}{E+mc^2}\end{bmatrix}\\ \end{align} \quad{\scriptsize (式28.18\text{a})}$
$\small \begin{align} u_2=\begin{bmatrix}\phi_2\\\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E+mc^2}\phi_2\end{bmatrix}=\begin{bmatrix}0\\1\\\frac{c}{E+mc^2}{\scriptsize\begin{bmatrix}p_3&p_1-\text ip_2\\p_1+\text ip_2&-p_3\end{bmatrix} \begin{bmatrix}0\\1\end{bmatrix}}\end{bmatrix}=\begin{bmatrix}0\\1\\\frac{p_1c-\text ip_2c}{E+mc^2}\\\frac{-p_3c}{E+mc^2}\end{bmatrix}\\ \end{align} \quad{\scriptsize (式28.18\text{b})}$
而当能量取负能解时,我们选取$ \small \chi $作为自由变量,并且利用$ \small \phi=K^{-1}\chi $给出本征态:
$\small \begin{align} v_1=\begin{bmatrix}\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E-mc^2}\chi_1\\\chi_1\end{bmatrix}=\begin{bmatrix}\frac{p_3c}{E-mc^2}\\\frac{p_1c+\text ip_2c}{E-mc^2}\\1\\0\end{bmatrix}\\ \\ v_2=\begin{bmatrix}\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E-mc^2}\chi_2\\\chi_2\end{bmatrix}=\begin{bmatrix}\frac{p_1c-\text ip_2c}{E-mc^2}\\\frac{-p_3c}{E-mc^2}\\0\\1\end{bmatrix}\\ \end{align} \quad{\scriptsize (式28.19)}$
这样,我们就完成了能量本征值和本征态的求解,接下来可以讨论它们的物理意义了。
注1:如果直接用Matlab求解,Matlab会对所有本征态都默认选取$ \small \chi $为自由变量,不方便我们讨论解的物理意义。
注2:别忘了,完整的解还要在$ \small u_1,u_2,v_1,v_2 $后面乘上一个复指数函数。
2) 负能解与反粒子
首先来说说能量本征值的物理意义。
从能量本征值解的结果可以看到,狄拉克方程的解同样出现了负能解$ \small E_3,E_4 $,看来狄拉克方程也同样存在K-G方程的负能解问题。
既然问题无法回避,又不能解决提出问题的人(毕竟狄拉克不能自己解决自己),那就想办法把它合理化,顺水推舟提出个新理论(再顺手领个诺奖)。
问了更好理解狄拉克的解释,我们不妨想象,有一个提问者和狄拉克之间,在用一问一答的方式讨论负能态问题:
问:负能态真的存在吗?
狄:我相信我的方程没有错,所以我相信它存在。
问:那为什么我们从来观察不到电子往负能态跃迁呢?
狄:因为在真空状态下,负能级已经被电子填满了,根据泡利不相容原理,它无法再容下新的电子。
问:那负能级的电子会不会向上跃迁呢?
狄:会。
问:那这时候不就空出一个位子来了吗?
狄:是的,而且这个空穴会有和负能量电子完全互补的一套物理量:正的能量、正的质量和正的电荷。换句话说,真空受到能量激发后,会产生一个普通的电子(从负能态跃迁到正能态)和一个具有正能量、正质量、正电荷的空穴,我们不妨将这个空穴叫做正电子(positive electron)。反过来,如果电子跃迁回负能态空穴,那么这个空穴就会被重新填满,这个时候我们就会观察到电子$-$正电子对发生湮灭,同时放出两份电子的能量。
问:那为什么我们没观察到你所说的正电子呢?
狄:等几年吧,时间会给出答案的。
而狄拉克没有等太久,两年后的1930年,中国物理学家赵忠尧发现了γ射线在重原子核附近的反常能量损失,以及γ射线被散射时出现的与电子能量相当的新的反常γ光子(正负电子对湮灭),可惜他当时并不知道关于正电子的预言,没有进行进一步的验证。
而他的同学安德森受到他的实验结果启发,在1932年通过一个让宇宙射线穿过云室的实验,观察到了正电子的轨迹,从而证实了正电子的存在,并且与四年后喜提诺奖。
而正电子理论也因此成为狄拉克方程带来的第一个重大突破。
现在说完了本征值,我们将注意力放到更有意思的本征态上。
首先,根据负能态的意义,我们不难得知,狄拉克方程的四个本征态中,$ \small u_1,u_2 $代表正能态、也就是正粒子的解,而$ \small v_1,v_2 $代表着负能态、也就是反粒子的解,它们在有着很多截然相反的物理特性和空间特性,我们会在未来的课程里慢慢讨论。
现在我们只关心这些本征态中包含的一个信息:
在上节课追随狄拉克的脚步构建方程的过程中,我们曾经引入了泡利算符,这似乎意味着,狄拉克方程以及它的本征态中应该天然包含自旋信息。
接下来我们来看看是不是这样。
3) 自旋的引入
我们在第26课曾经提到,非相对论情形下,自旋和动量、位置等经典力学量互不相干,完全是一个独立的自由度,在理论上也是可有可无,只是因为实验观测到了能级分裂才“被迫”引入。
但是接下来我们将看到,在狄拉克方程中,自旋的引入在理论上也是物理上的必然。
这要从角动量的守恒律说起。
我们知道,在经典图像中,一个受球对称场作用、或者完全不受任何外场作用的物体的角动量应该是守恒的。
而在量子力学中,这条定律也被保留了下来,不过,由于粒子的状态往往并不处在角动量的本征态上,因此量子版本的角动量守恒,应该是角动量的期望值不随时间变化,即:
$\small\begin{align} \frac{\text d\left<\boldsymbol J\right>}{\text dt}&=0 \end{align}\quad\scriptsize{(式28.20)}$
其中$ \small \boldsymbol J $代表角动量。
现在,请同学们回忆起我们在第14课讨论动量期望值随时间变化的时候,提到过的一个式子:
$\small\begin{align} \frac{\text d\left<p\right>}{\text dt}&=\frac{1}{\text i\hbar}\left<\psi\right|\left(\hat{p}\hat{H}-\hat{H}\hat{p}\right)\left|\psi\right>\ &=\frac{1}{\text i\hbar}\left<\psi\right|\left[\hat p,\hat H\right]\left|\psi\right> \end{align}\quad\scriptsize{(式14.18)}$
这个式子告诉我们,动量期望值随时间的变化与动量算符和哈密顿算符的对易子$ \small \left[\hat p,\hat H\right] $有关,如果动量算符与哈密顿算符对易,则动量期望值将不随时间变化,即:
$\small \begin{align} \left[\hat p,\hat H\right]=0\ \Rightarrow\ \frac{\text d\left<p\right>}{\text dt}&=0 \end{align} \quad{\scriptsize(式28.21)}$
而今后讨论量子力学中的对称性时,我们将证明,这个关系可以推广到任意力学量上面:如果一个力学量算符$ \small \hat F $与哈密顿算符对易,那么这个力学量将是守恒的。
回到角动量,在一个量子力学系统里,角动量要守恒,就必须有:
$\small \begin{align} \left[\hat {\boldsymbol J},\hat H\right]=0 \end{align} \quad{\scriptsize(式28.22)}$
注意:角动量是矢量,因此这个对易关系其实包含了三个角动量分量分别与哈密顿算符对易的关系。
如果不考虑粒子的自旋,那么它的角动量将只包含轨道角动量$ \small \boldsymbol L=\boldsymbol r\times \boldsymbol p $(就像一个没有自转的经典粒子)
我们在第19课已经证明,非相对论情形下,球对称场中粒子轨道角动量的三个分量$ \small \hat L_x,\hat L_y,\hat L_z $的确是分别与哈密顿算符对易的,而自由粒子可以看成$ \small V(r)\equiv 0 $的特殊情形,因此轨道角动量也天然地与哈密顿量对易。
但是如果来到相对论情形、考虑狄拉克方程中的哈密顿算符,一切就不一样了。
我们先将轨道角动量展开写成位置和动量的算符的函数:
$\small \begin{align} \hat {\boldsymbol L}&=\left(\hat L_x,\hat L_y,\hat L_z\right)\\ &=\left(\hat y\hat p_z-\hat z\hat p_y,\hat z\hat p_x-\hat x\hat p_z,\hat x\hat p_y-\hat y\hat p_x\right)\ \end{align} \quad{\scriptsize(式28.23)}$
另一方面,从狄拉克方程中:
$\small \begin{align} \text i\hbar\frac{\partial \psi}{\partial t}&=\left(\alpha_1\hat p_xc+\alpha_2\hat p_yc+\alpha_3\hat p_zc+\beta mc^2\right)\psi\ \end{align} \quad{\scriptsize (式27.16)}$
可以导出粒子的哈密顿算符:
$\small \begin{align} \hat H&=\alpha_1\hat p_xc+\alpha_2\hat p_yc+\alpha_3\hat p_zc+\beta mc^2\ \end{align} \quad{\scriptsize (式28.24)}$
接下来,我们来计算角动量与哈密顿量的对易子。
以$ \small \hat L_z $为例:
$\small \begin{align} \left[\hat L_z,\hat H\right]&=\left[\hat x\hat p_y-\hat y\hat p_x,\alpha_1\hat p_xc+\alpha_2\hat p_yc+\alpha_3\hat p_zc+\beta mc^2\right]\ \end{align} \quad{\scriptsize (式28.25)}$
根据第19课给出的公式19.4,我们可以将上式拆成8组对易子之和:
$\small \begin{align} \left[\hat L_z,\hat H\right]&=\ \ \left[\hat x\hat p_y,\alpha_1\hat p_xc\right]+\left[\hat x\hat p_y,\alpha_2\hat p_yc\right]+\left[\hat x\hat p_y,\alpha_3\hat p_zc\right]+\left[\hat x\hat p_y,\beta mc^2\right]\\ &\quad-\left[\hat y\hat p_x,\alpha_1\hat p_xc\right]-\left[\hat y\hat p_x,\alpha_2\hat p_yc\right]-\left[\hat y\hat p_x,\alpha_3\hat p_zc\right]-\left[\hat y\hat p_x,\beta mc^2\right] \end{align} \quad{\scriptsize (式28.26)}$
其中第2、3、5、7项等于0(将$ \small \alpha_i $视为常数,再通过第19课给出的式19.5和19.34推导得出)、而第4项和第8项中,可以将$ \small \beta mc^2 $视作常数(它们和坐标、动量都无关),因此上式只剩下第1项和第6项:
$\small \begin{align} \left[\hat L_z,\hat H\right]&=\left[\hat x\hat p_y,\alpha_1\hat p_xc\right]-\left[\hat y\hat p_x,\alpha_2\hat p_yc\right]\\ &=\alpha_1c\hat x\left[\hat p_y,\hat p_x\right]+\left[\hat x,\hat p_x\right]\alpha_1c\hat p_y-\alpha_2c\hat y\left[\hat p_x,\hat p_y\right]-\left[\hat y,\hat p_y\right]\alpha_2c\hat p_x\\ &=0+\text i\hbar\alpha_1c\hat p_y-0-\text i\hbar\alpha_2c\hat p_x\\ &=\text i\hbar c\left(\alpha_1\hat p_2-\alpha_2\hat p_1\right)\ \end{align} \quad{\scriptsize (式28.27)}$
最后一步无论如何都不可能等于0,因此$ \small \hat L_z,\hat H $不对易。
同理可得轨道角动量的其他分量与哈密顿算符的对易子,最终整理如下:
$\small \left\{\begin{align} \left[\hat L_x,\hat H\right]&=\text i\hbar c\left(\alpha_2\hat p_3-\alpha_3\hat p_2\right)\\ \left[\hat L_y,\hat H\right]&=\text i\hbar c\left(\alpha_3\hat p_1-\alpha_1\hat p_3\right)\\ \left[\hat L_z,\hat H\right]&=\text i\hbar c\left(\alpha_1\hat p_2-\alpha_2\hat p_1\right)\\ \end{align} \right. \quad{\scriptsize (式28.28)}$
总结成矢量式就是:
$\small \begin{align} \left[\hat {\boldsymbol L},\hat H\right]&=\text i\hbar c\left(\boldsymbol\alpha\times\boldsymbol p\right)\ \end{align} \quad{\scriptsize (式28.29)}$
这就意味着,轨道角动量不是一个守恒量,那怎么补救这个守恒律呢?
我们可以尝试着引入粒子的“自转”,然后看看总角动量是否守恒,而这个“自转”自然就是粒子的自旋了(虽然并没有真的在转)。
不过现在有个问题:自旋算符是三个2×2矩阵,但狄拉克方程的解是4×1的,没法直接作用。
为了匹配,我们将自旋算符简单扩充一下,变成这样的4×4分块对角矩阵:
$\small \left\{\begin{align} \hat S_{x}^{(\text{D})}&=\begin{bmatrix}\hat S_{x}&O\\O&\hat S_{x}\end{bmatrix} =\frac{\hbar}{2}\begin{bmatrix}0&1&0&0\\1&0&0&0\\0&0&0&1\\0&0&1&0\end{bmatrix} \\ S_{y}^{(\text{D})}&=\begin{bmatrix}\hat S_{y}&O\\O&\hat S_{y}\end{bmatrix} =\frac{\hbar}{2}\begin{bmatrix}0&-\text i&0&0\\\text i&0&0&0\\0&0&0&-\text i\\0&0&\text i&0\end{bmatrix} \\ S_{z}^{(\text{D})}&=\begin{bmatrix}\hat S_{z}&O\\O&\hat S_{z}\end{bmatrix} =\frac{\hbar}{2}\begin{bmatrix}1&0&0&0\\0&-1&0&0\\0&0&1&0\\0&0&0&-1\end{bmatrix} \\ \end{align}\right. \quad{\scriptsize (式28.30)}$
然后我们来看看它们在物理意义上是否符合自旋的特征。
仍然以$ \small S_{z}^{(\text{D})} $为例:
$\small \begin{align} \left[\hat S_{z}^{(\text{D})},\hat H\right]&=\begin{bmatrix}S_z&O\\O&S_z\end{bmatrix}\begin{bmatrix}mc^2I&\boldsymbol\sigma\cdot\boldsymbol pc\\\boldsymbol\sigma\cdot\boldsymbol pc&-mc^2I\end{bmatrix}-\begin{bmatrix}mc^2I&\boldsymbol\sigma\cdot\boldsymbol pc\\\boldsymbol\sigma\cdot\boldsymbol pc&-mc^2I\end{bmatrix}\begin{bmatrix}S_z&O\\O&S_z\end{bmatrix}\\ &=\begin{bmatrix}mc^2S_z&S_z\boldsymbol\sigma\cdot\boldsymbol pc\\S_z\boldsymbol\sigma\cdot\boldsymbol pc&-mc^2S_z\end{bmatrix}-\begin{bmatrix}mc^2S_z&\boldsymbol\sigma S_z\cdot\boldsymbol pc\\\boldsymbol\sigma S_z\cdot\boldsymbol pc&-mc^2S_z\end{bmatrix}\\ &=\begin{bmatrix}O&\left(S_z\boldsymbol\sigma -\boldsymbol\sigma S_z\right)\cdot\boldsymbol pc\\\left(S_z\boldsymbol\sigma -\boldsymbol\sigma S_z\right)\cdot\boldsymbol pc&O\end{bmatrix}\\ \end{align} \quad{\scriptsize (式28.31)}$
而$ \small \boldsymbol \sigma=\frac{2}{\hbar}\boldsymbol S $,由三个泡利矩阵分量构成,于是:
$\small \begin{align} S_z\boldsymbol\sigma -\boldsymbol\sigma S_z&=\left(S_z\sigma_x-\sigma_xS_z,S_z\sigma_y-\sigma_yS_z,S_z\sigma_z-\sigma_zS_z\right)\\ &=\frac{2}{\hbar}\left([S_z,S_x],[S_z,S_y],[S_z,S_z]\right)\ \end{align} \quad{\scriptsize (式28.32)}$
根据第26课给出的三个自旋分量的对易关系(式26.14),可得:
$\small \begin{align} S_z\boldsymbol\sigma -\boldsymbol\sigma S_z&=\frac{2}{\hbar}\left(\text i\hbar S_y,-\text i\hbar S_x,0\right)\\ &=\text i\hbar\left(\sigma_y,-\sigma_x,0\right)\ \end{align} \quad{\scriptsize (式28.33)}$
将其代回式28.31,可得:
$\small \begin{align} \left[\hat S_{z}^{(\text{D})},\hat H\right]&=\text i\hbar c\begin{bmatrix}O&-\left(\sigma_xp_y-\sigma_yp\right)\\-\left(\sigma_xp_y-\sigma_yp\right)&O\end{bmatrix}\\ &=-\text i\hbar c\left(\begin{bmatrix}O&\sigma_x\\\sigma_x&O\end{bmatrix}p_y-\begin{bmatrix}O&\sigma_y\\\sigma_y&O\end{bmatrix}p_x\right)\\ &=-\text i\hbar c\left(\alpha_1p_2-\alpha_2p_1\right)\\ \end{align} \quad{\scriptsize (式28.34)}$
同理可得其他分量,最后汇总为:
$\small \left\{\begin{align} \left[\hat S_{x}^{(\text{D})},\hat H\right]&=-\text i\hbar c\left(\alpha_2\hat p_3-\alpha_3\hat p_2\right)\\ \left[\hat S_{y}^{(\text{D})},\hat H\right]&=-\text i\hbar c\left(\alpha_3\hat p_1-\alpha_1\hat p_3\right)\\ \left[\hat S_{z}^{(\text{D})},\hat H\right]&=-\text i\hbar c\left(\alpha_1\hat p_2-\alpha_2\hat p_1\right)\\ \end{align} \right. \quad{\scriptsize (式28.35)}$
以及总的矢量式:
$\small \begin{align} \left[\hat {\boldsymbol S}^{(\text{D})},\hat H\right]&=-\text i\hbar c\left(\boldsymbol\alpha\times\boldsymbol p\right)\ \end{align} \quad{\scriptsize (式28.36)}$
将式28.29和式28.36相加,我们将得到一个非常喜人的结果:
$\small \begin{align} \left[\hat {\boldsymbol L},\hat H\right]+\left[\hat {\boldsymbol S},\hat H\right]&=\text i\hbar c\left(\boldsymbol\alpha\times\boldsymbol p\right)-\text i\hbar c\left(\boldsymbol\alpha\times\boldsymbol p\right)=\boldsymbol 0\ \end{align} \quad{\scriptsize(式28.37)}$
从这里开始,我们省略右上标$(D)$,默认$ \small \hat {\boldsymbol S} $为狄拉克语境下的自旋算符。
也就是:
$\small \begin{align} \left[\hat {\boldsymbol L}+\hat {\boldsymbol S},\hat H\right]=\boldsymbol 0\ \end{align} \quad{\scriptsize(式28.38)}$
这简直太妙了!
这意味着,轨道和自旋合成的总角动量算符和哈密顿量对易,也就意味着总角动量是守恒的,也就是说,我们从狄拉克方程出发、结合角动量守恒这个朴素的原理、非常自然地引出了自旋,而不是像非相对论情形那样强加上去。
此外,这样定义的自旋和非相对论情形还有一个令人惊奇的不同之处,我们马上来看看。
4) 自旋方向与螺旋度
我们在第26课提到,非相对论情形下,自旋和波函数是独立的,这意味着,一个粒子可以同时具有某个方向$ \small \boldsymbol n_p $上确定的动量和另一个方向$ \small \boldsymbol n_s $上确定的自旋,动量方向和自旋方向互不干扰。
但是在狄拉克方程解的波函数中,事情发生了一些变化。
由于空间各个方向的均一性,我们不妨选取自旋方向为$z$方向,然后看看,处于任意方向动量本征态的例子,能否都同时具有确定的$z$方向的自旋。
以正能解$ \small u_1 $为例,将自旋算符$ \small \hat S_z $作用在式$28.18$中给出的$ \small u_1 $上,并假设 $\small u_1$ 是$ \small \hat S_z $的本征态,于是有:
$\small \begin{align} \hat S_{z}u_1&=\frac{\hbar}{2}\begin{bmatrix}1&0&0&0\\0&-1&0&0\\0&0&1&0\\0&0&0&-1\end{bmatrix} \begin{bmatrix}1\\0\\\frac{p_3c}{E+mc^2}\\\frac{p_1c+\text ip_2c}{E+mc^2}\end{bmatrix}=\frac{\hbar}{2}\begin{bmatrix}1\\0\\\frac{p_3c}{E+mc^2}\\-\frac{p_1c+\text ip_2c}{E+mc^2}\end{bmatrix} \end{align} \quad{\scriptsize (式28.39)}$
比较$ \small u_1 $和上式最右边,可以看到,除非$ \small p_1+\text ip_2=0 $、也就是$ \small p_1=p_2=0 $,否则$ \small \hat S_{z}u_1\neq \frac{\hbar}{2}u_1$
同理可证,$ \small u_2 $以及$ \small u_1,u_2 $的任意线性组合(也是正能解)、以及$ \small v_1,v_2 $的任意线性组合,都不是$ \small \hat S_z $的本征态,除非$ \small p_1=p_2=0 $(同学们可以自己动手证明一遍)。
而$ \small p_1=p_2=0 $意味着动量只有$z$分量,也就是说,动量方向和自旋方向必须一致。
反过来,当粒子的状态位于动量$ \small \left(p_1,p_2,p_3\right) $的本征态时,其对应的自旋态也只能是$ \small \boldsymbol n_p=\frac{1}{p}\left(p_1,p_2,p_3\right) $方向的自旋,即:
$\small \begin{align} \hat h_{\boldsymbol p}&=\hat {\boldsymbol S}\cdot \frac{\boldsymbol p}{|p|}\\&=\frac{1}{|p|}\left(\hat S_1p_1+\hat S_2p_2+\hat S_3p_3\right)\\ &=\frac{\hbar}{2|p|}\begin{bmatrix}p_3&p_1-\text ip_2&0&0\\p_1+\text ip_2&-p_3&0&0\\0&0&p_3&p_1-\text ip_2\\0&0&p_1+\text ip_2&-p_3\end{bmatrix} \end{align} \quad{\scriptsize (式28.40)}$
可以证明,$ \small u_1,u_2 $以及$ \small v_1,v_2 $的下列线性组合都是$ \small \small \hat h_{\boldsymbol p} $的本征态:
$\small \left\{\begin{align} u_+&=\cos\frac{\theta}{2}u_1+\text e^{\text i\varphi}\sin\frac{\theta}{2}u_2\\ u_-&=-\sin\frac{\theta}{2}u_1+\text e^{\text i\varphi}\cos\frac{\theta}{2}u_2\\ v_+&=\cos\frac{\theta}{2}v_1+\text e^{\text i\varphi}\sin\frac{\theta}{2}v_2\\ v_-&=-\sin\frac{\theta}{2}u_1+\text e^{\text i\varphi}\cos\frac{\theta}{2}u_2\\ \end{align}\right. \quad{\scriptsize(式28.41)}$
其中$ \small \theta,\varphi $满足:
$\small \cos\theta=\frac{p_1}{\sqrt{p_1^2+p_2^2}},\ \sin\theta=\frac{p_2}{\sqrt{p_1^2+p_2^2}},\ \cos\varphi=\frac{p_3}{|p|} \quad{\scriptsize(式28.42)}$
以上证明请同学们动手试一试。
提示:利用下列关系式:
$\small \begin{align} a_1u_1+a_2u_2&=a_1\begin{bmatrix}\phi_1\\\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E+mc^2}\phi_1\end{bmatrix}+a_2\begin{bmatrix}\phi_2\\\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E+mc^2}\phi_2\end{bmatrix}\\ &=\begin{bmatrix}a_1\phi_1+a_2\phi_2\\\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E+mc^2}\left(a_1\phi_1+a_2\phi_2\right)\end{bmatrix}\\ &=\begin{bmatrix}\phi\\\frac{\boldsymbol\sigma\cdot\boldsymbol pc}{E+mc^2}\phi\end{bmatrix}\\ \end{align} \quad{\scriptsize (式28.43)}$
其中$ \small \phi=\begin{bmatrix}a_1\\a_2\end{bmatrix}$
然后利用分块矩阵运算,就能更快得出结果。
另外,推导时请注意区分狄拉克方程解中的分量$ \small \phi $和自旋方向中的相位角$ \small \varphi$
而这里新定义的力学量:
$\small \hat h_{\boldsymbol p}=\hat {\boldsymbol S}\cdot \frac{\boldsymbol p}{|p|} \quad{\scriptsize(式28.44)}$
叫做螺旋度(helicity,请注意与普朗克常数$ \small h $区分)。它和自旋一样,有$ \small \pm\frac{\hbar}{2} $两个本征值。如果将自旋直观想象成“自转”,那么螺旋度可以看成粒子在前进方向上的“旋进”,两个本征值对应的物理图景可以直观表示成下图的样子:
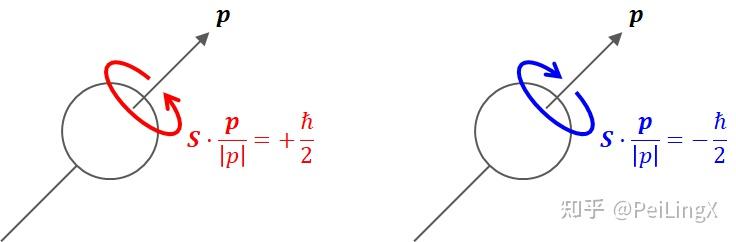
再次提醒:粒子并不是真的在“转”
这样一来,自旋就不再是那个随便摆出什么姿态都不会影响到其他力学量状态的“透明人”,而是和动量等经典力学量紧密结合在一起,成为整个波函数中不可或缺的一部分。
这里请同学们思考一个问题:
假设参考系$A$中的观测者张三,观察到一个粒子具有$z$方向的动量以及$z$方向的自旋本征态,而参考系$B$相对于参考系$A$沿$x$方向运动,那么对于参考系$B$中的观测者李四而言,粒子的自旋态还是$z$方向的自旋本征态吗?
而自旋的这一特殊方向性,也可以尝试从物理意义的角度去理解(以下为个人心得,不一定正确,如有偏差还请路过的各位大佬指出):
考虑一个处于能量本征态(也是动量本征态)的自由粒子。
当自旋方向与动量方向不一致时,如果选定了某个原点,那么动量和粒子坐标将形成轨道角动量,但是坐标和动量不能同时确定,因此轨道角动量$ \small \boldsymbol L $也就没有确定值(这也就对应了轨道角动量和哈密顿算符不对易的事实),而总角动量$ \small \boldsymbol J $和哈密顿算符对易、具有确定值,那么自旋$ \small \boldsymbol S=\boldsymbol J-\boldsymbol L $也就没有确定值了;
但是当自旋方向与动量方向一致时,动量在自旋所在平面上投影为0(如果将自旋想象成自转的话),于是该方向上的轨道角动量分量也就确定是0,此时该方向上自旋角动量就是总角动量,天然与哈密顿算符对易,也就有了确定的自旋本征态。
当然,当粒子的“速度”远小于光速时($ \small |p|\ll mc $时),四个本征态近似变成:
$\small u_1,u_2\simeq\begin{bmatrix}\phi\\ \boldsymbol 0\end{bmatrix},v_1,v_2\simeq\begin{bmatrix}\boldsymbol 0\\ \chi\end{bmatrix} \quad{\scriptsize(式28.45)}$
由于自由变量$ \small \phi,\chi $可以任意选取,且$ \small \boldsymbol \sigma\boldsymbol 0=\boldsymbol 0 $,因此这些状态又可以取成任意方向自旋的本征态,不再受动量方向的影响,此时就又回到了非相对论的近似情形。
【练习】考虑一个处于动量本征态的电子,动量本征值为:
$\small \left(p_1,p_2,p_3\right)=\left(0,0,\frac{c}{1000}\right)$
电子的状态为:
$\small \psi=\frac{1}{\sqrt{2}}u_1+\frac{1}{\sqrt{2}}u_2$
如果对电子测量$x$方向的自旋,得到本征值$ \small +\frac{\hbar}{2} $的概率是多少?
5) 小结与预告
这节课,我们完成了自由粒子狄拉克方程的求解过程,并且跟随大师的意识流看到了反粒子概念的诞生,接下来,我们从方程出发、结合角动量守恒这样朴素的原理,用更自然地方式导出了自旋,并且看到了它和动量之间密不可分的联系,从而体验到了相对论情形下自旋存在的必然性(而不再是非相对论情形下理论上可有可无的东西)。
到此为止,我们对狄拉克方程的讨论就告一段落了,接下来,我们要开启一段新的话题:体验蕴藏在量子力学中的各种精巧的对称性。
不过这里需要提前向一直追更的同学们道个歉:新的内容更新可能又要等到半年以后。
一是因为我对这部分内容还不能轻松驾驭,还需要更多的学习和整理;
二是因为接下来的半年里,我将开启(挖)一个关于量子计算的新系列(新坑)。这个话题源自于去年年底出现的一些机缘巧合,这接近一年的时间里,我花了很多时间和精力来自学,这也是为什么这个系列第28课拖更这么长时间。
虽然我挖的坑有点多,但我保证这个新坑一定会在半年内填完,然后回到咱们的量子力学系列来。这段时间也欢迎同学们关注我的新系列。
量子计算学习心得(0):序言与目录
补遗:
我们在上节课曾经提到过一个问题:
狄拉克方程定义的概率流密度
$\small \begin{align} \boldsymbol j=c\left(\psi^\dagger\alpha_1\psi,\ \psi^\dagger\alpha_2\psi,\ \psi^\dagger\alpha_3\psi\right) \end{align}$
能否化为更直观的“速度乘以概率密度”的形式:
$\small \begin{align} \boldsymbol j&=\psi^\dagger\psi\left(\frac{p_x}{m},\frac{p_y}{m},\frac{p_z}{m}\right)\\ &=\rho\left(\frac{p_x}{m},\frac{p_y}{m},\frac{p_z}{m}\right) \end{align} \quad{\scriptsize (式27.37)}$
当时我们给出了肯定的回答。
但是在没有给出狄拉克方程解的具体形式之前,我们还无法将两种形式联系起来,而现在有了方程解的形式、具体说是式28.7给出的形式,就理解推导过程了。
具体推导过程在这篇文章里:
有兴趣的同学可以读一读。
编辑于 2023-10-30 11:33・IP 属地四川
