PeiLingX
物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》第27课。
了解本系列及本专栏其他文章，请收藏目录：
0) 开篇语
经过几节课的准备，我们终于要开始慢慢认识“物理学史上最伟大开根号”之狄拉克方程了。
不过这不是一节课能完成的事情，这节课里我们会先梳理方程的构造过程，然后看看它是否解决了克莱因$-$高登方程那个让人困惑的负概率问题，并且顺便再体验一把相对论框架下的对称性。到了下节课，我们会尝试找出方程最简单的解，顺便从中窥探一个新的空间，并且在下一章里对这个新的空间进行更深的认识。
⚠ 枯燥预警：这个方程的构造过程看起来更像是一个数学把戏，会显得比较枯燥，并且微分方程和矩阵方程交杂到一起的形式理解起来也会有些困难(特别是在一些等式的推导过程中)。不过以后我们回顾这里面蕴含的空间结构时，会理清楚它们的玄妙之处，只是这节课里我们还得先忍受一下这种枯燥和不适应感。
1) 方程构造：第一次尝试
我们在第25课中提到，狄拉克构造新的方程的动机，是要解决K-G方程的负概率问题，而解决这个问题的关键是使方程对时间的导数回到一阶，也就是这样的形式：
$\small \begin{align} \text i\hbar\frac{\partial \psi}{\partial t}=E\psi=\left(\alpha\hat pc+\beta mc^2\right)\psi \end{align} \quad{\scriptsize (式27.1)}$
注意：由于动量是三维的，而左右两边都应该是标量(因为左边的能量是标量)，因此右边第一项其实是一个“向量”$ \small \boldsymbol\alpha $和三维动量算符$ \small \hat {\boldsymbol p} $的内积：
$\small \boldsymbol\alpha\cdot\hat {\boldsymbol p}=\alpha_1\hat p_1+\alpha_2\hat p_2+\alpha_3\hat p_3 \quad{\scriptsize (式27.2)}$
而为了满足相对论能量关系，我们希望等号右边取平方后变成：
$\small \begin{align} \left(c\boldsymbol \alpha\cdot \hat{\boldsymbol p}+\beta mc^2\right)^2=\hat p^2c^2+m^2c^4 \end{align} \quad{\scriptsize (式27.3)}$
将上式的左边展开，就是：
$\small \begin{align} \left(c\boldsymbol \alpha\cdot \hat{\boldsymbol p}+\beta mc\right)^2&=\left(\alpha_1\hat p_1c+\alpha_2\hat p_2c+\alpha_3\hat p_3c+\beta mc^2\right)^2\\ &=\alpha_1^2\hat p_1^2c^2+\alpha_2^2\hat p_2^2c^2+\alpha_3^2\hat p_3^2c^2+\beta^2m^2c^4\\ &\quad{\scriptsize +\left(\alpha_1\alpha_2+\alpha_2\alpha_1\right)\hat p_1\hat p_2c^2+\left(\alpha_2\alpha_3+\alpha_3\alpha_2\right)\hat p_2\hat p_3c^2+\left(\alpha_3\alpha_1+\alpha_1\alpha_3\right)\hat p_3\hat p_1c^2}\\ &\quad{\scriptsize +\left(\alpha_1\beta+\beta\alpha_1\right)\hat p_1mc^3+\left(\alpha_2\beta+\beta\alpha_2\right)\hat p_2mc^3+\left(\alpha_3\beta+\beta\alpha_3\right)\hat p_3mc^3} \end{align} \quad{\scriptsize (式27.4)}$
对比式27.3的右边，我们可以导出$ \small \boldsymbol \alpha,\beta $需要满足的一组条件：
$\small \begin{cases} 条件\text a:&\alpha_i^2=I&i=1,2,3&(\alpha_i^2\hat p_i^2=\hat p_i^2)\\ 条件\text b:&\beta^2=I&&(\beta^2m^2c^2=m^2c^2)\\ 条件\text c:&\alpha_i\alpha_j+\alpha_j\alpha_i=O&i\neq j&(交叉项\hat p_i\hat p_j系数为零)\\ 条件\text d:&\alpha_i\beta+\beta\alpha_i=O&i=1,2,3&(交叉项\hat p_imc系数为零) \end{cases} \quad{\scriptsize (式27.5)}$
显然，如果$ \small \alpha_i $是标量，那么我们将没办法找到同时满足上面四个条件的实数或复数。
所以唯一的解决方案就是：假设$ \small \beta,\alpha_i $是矩阵，然后找出它们。
对于条件$a$和$c$，如果我们回忆起上节课的式26.16，会发现，三个泡利矩阵天然满足这一点，即：
$\small \sigma_1^2=\sigma_2^2=\sigma_3^2=I \quad{\scriptsize (式27.6)}$
而且也满足：
$\small \sigma_i\sigma_j+\sigma_j\sigma_i=0$
所以接下来的事情看起来也很简单：基于三个泡利矩阵，利用条件$d$，找出$ \small \beta $的矩阵形式就完事儿了。
但实际上，如果我们选择了$ \small \alpha_i=\sigma_i $，那么最后求出的$ \small \beta $将会是零矩阵。
我们来简单推导一下。
首先，我们假设：
$\small \beta=\begin{bmatrix}u_{11}+\text iv_{11}&u_{12}+\text iv_{12}\\ u_{21}+\text iv_{21}&u_{22}+\text iv_{22} \end{bmatrix} \quad{\scriptsize (式27.7)}$
而稍加分析我们会发现，其实任意复2×2矩阵都可以分解为单位矩阵和三个泡利矩阵的线性组合：
$\small \begin{align} \beta&=b_0\begin{bmatrix}1&0\\0&1\end{bmatrix}+b_1\begin{bmatrix}0&1\\1&0\end{bmatrix}+b_2\begin{bmatrix}0&-\text i\\ \text i&0\end{bmatrix}+b_3\begin{bmatrix}1&0\\0&-1\end{bmatrix}\\ &=b_0I+b_1\sigma_1+b_2\sigma_2+b_3\sigma_3 \end{align} \quad{\scriptsize (式27.8)}$
其中：
$\small \begin{cases} b_0=\frac{u_{11}+u_{22}}{2}+\text i\frac{v_{11}+v_{22}}{2}\\ b_1=\frac{u_{12}+u_{21}}{2}+\text i\frac{v_{12}+v_{21}}{2}\\ b_2=\frac{v_{21}-v_{12}}{2}+\text i\frac{u_{12}-u_{21}}{2}\\ b_3=\frac{u_{11}-u_{22}}{2}+\text i\frac{v_{11}-v_{22}}{2}\\ \end{cases} \quad{\scriptsize (式27.9)}$
也就是说，任意一个2×2的复数矩阵都可以表示成$ \small \left\{I,\sigma_1,\sigma_2,\sigma_3\right\} $这组基底的线性组合，这样表示的好处是可以利用泡利矩阵的性质直接算$ \small \beta$
比如，将矩阵$ \small \beta $代入条件$d$，我们将得到：
$\small \begin{align} O&=\alpha_1\beta+\beta\alpha_1\\&=\sigma_1\left(b_0I+b_1\sigma_1+b_2\sigma_2+b_3\sigma_3\right)+\left(b_0I+b_1\sigma_1+b_2\sigma_2+b_3\sigma_3\right)\sigma_1\\ &=2b_0\sigma_1+2b_1I+b_2\left(\sigma_1\sigma_2+\sigma_2\sigma_1\right)+b_3\left(\sigma_1\sigma_3+\sigma_3\sigma_1\right)\\ &=2b_0\sigma_1+2b_1I\\ &=\begin{bmatrix}2b_1&2b_0\\2b_0&2b_1\end{bmatrix} \end{align} \quad{\scriptsize (式27.10)}$
并且解出：
$\small b_0=b_1=0 \quad{\scriptsize (式27.11)}$
再利用同样的操作，我们还能解出：
$\small b_2=b_3=0 \quad{\scriptsize (式27.12)}$
也就是说，$ \small \beta $是一个2×2的零矩阵。
这样一来，条件$b$、也就是$ \small \beta^2=I $，就不满足了，这也意味着方程中$ \small mc $那一项也随之消失了，这显然不符合物理事实。
不过好在狄拉克很快找到了解决办法：把泡利矩阵扩充一下就行了，扩充后的泡利矩阵有了更多的未知数，至少有了更多的选择。
2) 正确的方程
我们直接说结果：
扩充后的矩阵$ \small \alpha_1,\alpha_2,\alpha_3 $仍然各自由三个泡利矩阵组成，只不过它们是泡利矩阵分块组合而成的三个4×4矩阵，长这个样子：
$\small \alpha_i=\begin{bmatrix}O&\sigma_i\\ \sigma_i&O \end{bmatrix}\ (i=1,2,3) \quad{\scriptsize (式27.13)}$
展开写，就是：
$\small \begin{align} \alpha_1&={\scriptsize \begin{bmatrix}O&\sigma_1\\ \sigma_1&O \end{bmatrix}=\begin{bmatrix}0&0&0&1\\0&0&1&0\\0&1&0&0\\1&0&0&0 \end{bmatrix}}\\ \alpha_2&={\scriptsize \begin{bmatrix}O&\sigma_2\\ \sigma_2&O \end{bmatrix}=\begin{bmatrix}0&0&0&-\text i\\0&0&\text i&0\\0&-\text i&0&0\\ \text i&0&0&0 \end{bmatrix}} \\ \alpha_3&={\scriptsize \begin{bmatrix}O&\sigma_3\\ \sigma_3&O \end{bmatrix}=\begin{bmatrix}0&0&1&0\\0&0&0&-1\\1&0&0&0\\0&-1&0&0 \end{bmatrix}} \end{align} \quad{\scriptsize (式27.14)}$
很容易证明，它们仍然满足条件a和c。
而矩阵$ \small \beta $可以这样构造：
$\small \beta={\scriptsize \begin{bmatrix}I&O\\O&-I \end{bmatrix}=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&-1 \end{bmatrix}} \quad{\scriptsize (式27.15)}$
它的平方等于单位矩阵，这样就满足了条件b。
而它与三个$ \small \alpha_i $相乘时，由于对角上的$ \small I $和$ \small -I $符号相反，可以正好让左乘$ \small \alpha_i $和右乘$ \small \alpha_i $的结果相反(同学们可以动手算一下)，因此满足了条件d
这样，我们就重新构造出了狄拉克方程。
而如果将$ \small \beta,\alpha_1,\alpha_2,\alpha_3 $四个矩阵代入方程中：
$\small \begin{align} \text i\hbar\frac{\partial \psi}{\partial t}&=\left(\alpha_1\hat p_xc+\alpha_2\hat p_yc+\alpha_3\hat p_zc+\beta mc^2\right)\psi\ \end{align} \quad{\scriptsize (式27.16)}$
再将三个动量算符看作三个数，乘到矩阵$ \small \alpha_i $里面去，然后再将右边几个矩阵求和，我们就能得到完整的狄拉克方程的最终矩阵形式：
$\small \begin{align} \text i\hbar\frac{\partial }{\partial t}\begin{bmatrix}\psi_1\\\psi_2\\\psi_3\\\psi_4\end{bmatrix}&=\begin{bmatrix}mc^2&0&\hat p_zc&\hat p_xc-\text i\hat p_yc\\0&mc^2&\hat p_xc+\text i\hat p_yc&-\hat p_zc\\\hat p_zc&\hat p_xc-\text i\hat p_yc&-mc^2&0\\\hat p_xc+\text i\hat p_yc&-\hat p_zc&0&-mc^2\end{bmatrix}\begin{bmatrix}\psi_1\\\psi_2\\\psi_3\\\psi_4\end{bmatrix} \end{align} \quad{\scriptsize (式27.17)}$
· 由于方程中各算符以4×4矩阵形式呈现，因此相应的本征态也应该是一个4×1的矩阵，只不过它的四个分量不是常数，而仍然是时间和空间的波函数；
· 另外，可以证明，如果把等号右边那个矩阵平方一下，就可以变成一个4×4单位矩阵$ \small I_{4\times 4} $数乘$ \small p^2c^2+m^2c^4 $的结果，也就回到了相对论能量的平方关系，同学们可以自己动笔算一下。
到此，我们就跟随狄拉克的步伐，通过一组4×4矩阵的组合，开出了那个不带根号的伟大的“平方根”。
如果我们意识到方程解的分量个数，再联想到我们是在四维的相对论时空中讨论问题，那么同学们是不是会“很自然地”猜想：这个解也是个“四维向量”？
但这其实是一种误解：虽然方程解刚好也有4个分量，但它们并不是四维时空中的向量，因为以后我们会看到，它们在各类时空的几何变换中具有完全不同于四维向量的另一套变换规则，这也意味着它们存在于不同于四维时空的另一类空间中。
我们先记住它们的名字：这些具有四维列矩阵形式的解，被称为4分量“旋量”(Spinor)，它们所存在的空间也称作“旋量空间”，这个空间就是狄拉克方程呈现给我们的新世界，我们在未来还要慢慢认识它们。
那么话说回来，狄拉克方程中，四维时空中的“4”体现在哪里呢？我们可以先简单地认为，这个“4”体现在4个矩阵 $\small \left(\beta,\ \alpha_1,\ \alpha_2,\ \alpha_3\right) $的组合上(也就是说，体现在矩阵的个数、而不是维数上)，不久后我们会看到，对它们稍作变形，我们就能得到一个相对论味道更浓厚的方程形式。
当然，四维时空中的“4”和四分量旋量中的“4”虽然物理意义不同，但两者之间也不是毫无关联，这一点我们以后也会讨论到。
现在我们回来考虑下一个话题：
第25课中我们提到，构造这样一个一阶微分方程的最初动机，是为了解决负概率的问题，那么现在这个问题解决了吗？
为了寻找答案，我们不妨先来构造狄拉克方程的概率和概率流密度。
3) 概率流守恒
在经过第25课的热身之后，构造概率流密度的过程对我们来说也算是轻车熟路了。
首先，我们将原方程右边写成动量算符的坐标表象形式：
$\small \begin{align} \text i\hbar\frac{\partial }{\partial t}\psi&=-\text i\hbar c\left(\alpha_1\frac{\partial}{\partial x}+\alpha_2\frac{\partial}{\partial y}+\alpha_3\frac{\partial}{\partial z}\right)\psi+\beta mc^2\psi\end{align} \quad{\scriptsize (式27.18)}$
在这里，由于三个$ \small \alpha_i $是常数矩阵，因此它们可以交换顺序，这样，上式右边括号中的部分就可以写成：
$\small \begin{align} \left(\alpha_1\frac{\partial}{\partial x}+\alpha_2\frac{\partial}{\partial y}+\alpha_3\frac{\partial}{\partial z}\right)\psi&= \frac{\partial}{\partial x}\left(\alpha_1\psi\right)+\frac{\partial}{\partial y}\left(\alpha_2\psi\right)+\frac{\partial}{\partial z}\left(\alpha_3\psi\right) \end{align} \quad{\scriptsize (式27.19)}$
如果我们将$ \small \alpha_1\psi,\alpha_2\psi,\alpha_3\psi $看作某个三维向量的三个分量(虽然它们不是三个数而是三个4×1矩阵)，并且定义：
$\small \begin{align} \boldsymbol\alpha\psi&=\left(\alpha_1,\alpha_2,\alpha_3\right)\psi\\&=\left(\alpha_1\psi,\alpha_2\psi,\alpha_3\psi\right) \end{align} \quad{\scriptsize (式27.20)}$
那么我们还可以将方程右边第一项简写为梯度算子$ \small \boldsymbol\nabla $和向量$ \small \boldsymbol \alpha\psi $的内积：
$\small \begin{align} \text i\hbar\frac{\partial }{\partial t}\psi&=-\text i\hbar c\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)+\beta mc^2\psi \end{align} \quad{\scriptsize (式27.21)}$
接下来是第二步：对原方程两边取复共轭，找到它的共轭方程。
不过，这里需要注意的是，对于含有矩阵的微分方程而言，我们在取复共轭的同时，还要对矩阵取转置(就像我们在第2课讨论态矢量内积的时候所做的那样)，这样的操作叫做厄米共轭(Hermitian Conjugation)[1]，一个矩阵$ \small A $的厄米共轭记作 $\small A^\dagger$ (右上角那个符号读作$dagger$，因为它长得像一把剑)，我们以2×2矩阵为例，将厄米共轭的运算规则具体写出来就是：
$\small \left(\begin{bmatrix}a&\color{red}{b}\\\color{blue}{c}&d\end{bmatrix}\right)^\dagger=\begin{bmatrix}a^*&\color{blue}{c^*}\\\color{red}{b^*}&d^*\end{bmatrix} \quad{\scriptsize (式27.22)}$
(当然，这只是厄米共轭在矩阵形式的算符上的狭义定义，更严格的数学定义我们这里不讨论)
于是原方程的复共轭在形式上可以写为：
$\small \begin{align} -\text i\hbar\frac{\partial }{\partial t}\psi^\dagger&=\text i\hbar c\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger+mc^2\left(\beta\psi\right)^\dagger \end{align} \quad{\scriptsize (式27.23)}$
在这个式子中，$ \small \psi^\dagger $写出来就是：
$\small \psi^\dagger=\left(\begin{bmatrix}\psi_1\\\psi_2\\\psi_3\\\psi_4\end{bmatrix}\right)^\dagger=\begin{bmatrix}\psi_1^*&\psi_2^*&\psi_3^*&\psi_4^*\end{bmatrix} \quad{\scriptsize (式27.24)}$
这是一个1×4的行矩阵
其他几个矩阵$ \small \beta,\alpha_1,\alpha_2,\alpha_3 $的厄米共轭也是相同的操作，如果同学们动手算一下会发现，它们共轭转置后还是等于它们本身，即：
$\small \begin{cases} \beta^\dagger=\beta\ \alpha_i^\dagger=\alpha_i&(i=1,2,3) \end{cases} \quad{\scriptsize (式27.25)}$
还记得我们在第$x$课提到的厄米算符吗？对于物理上可观测的力学量而言，它们的算符都应该是厄米的，具有实的本征值(毕竟复数没办法观测到)。
而当一个算符以矩阵形式呈现时，我们就能很具体地从运算上识别出一个厄米算符来：它的厄米共轭正好等于它自身。并且我们可以证明，这样的矩阵具有实的特征值。
狄拉克方程中的$ \small \beta $和三个$ \small \alpha_i ($以及三个泡利矩阵$ \small \sigma_i )$就是这样的例子。
此外，由于共轭转置也是一种转置运算，根据转置运算的规则，我们还可以得出：
$\small (AB)^\dagger=B^\dagger A^\dagger \quad{\scriptsize (式27.26)}$
综合上面的信息，我们可以将式27.23右边第二项进一步化为：
$\small \begin{align} -\text i\hbar\frac{\partial }{\partial t}\psi^\dagger&=\text i\hbar c\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger+mc^2\left(\beta\psi\right)^\dagger\\ &=\text i\hbar c\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger+mc^2\psi^\dagger\beta^\dagger \\ &=\text i\hbar c\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger+mc^2\psi^\dagger\beta \end{align} \quad{\scriptsize (式27.27)}$
现在，我们将式27.21左乘$ \small \psi^\dagger $、式27.27右乘$ \small \psi $，可得：
$\small \begin{cases} \text i\hbar\psi^\dagger\frac{\partial }{\partial t}\psi=-\text i\hbar c\psi^\dagger\left[\boldsymbol\nabla\cdot\left(\boldsymbol \alpha\psi\right)\right]+mc^2\psi^\dagger\beta \psi&{\scriptsize (\text c)}\\ -\text i\hbar\left(\frac{\partial }{\partial t}\psi^\dagger\right)\psi=\text i\hbar c\left[\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger\right]\psi+mc^2\psi^\dagger\beta\psi&{\scriptsize (\text d)}\ \end{cases} \quad{\scriptsize (式27.28)}$
两式相减，并且两边消去$ \small \text i\hbar $，又可得：
$\small \begin{align} \psi^\dagger\frac{\partial \psi}{\partial t}+\frac{\partial \psi^\dagger}{\partial t}\psi=-\left(c\psi^\dagger\left(\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)\right)+c\left(\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger\right)\psi\right)\ \end{align} \quad{\scriptsize (式27.29)}$
这个方程的左边好处理，我们可以直接将它们合并成：
$\small \begin{align} \psi^\dagger\frac{\partial \psi}{\partial t}+\frac{\partial \psi^\dagger}{\partial t}\psi=\frac{\partial }{\partial t}\left(\psi^\dagger\psi\right)=\frac{\partial \rho}{\partial t} \end{align} \quad{\scriptsize (式27.30)}$
这样，概率密度随时间变化的项就出来了。
关键是右边，我们能不能将它化简成一个物理意义更明确的形式？
这里我们先写出结论(证明放到本文最后)：
$\small \begin{align} c\psi^\dagger\left[\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)\right]+c\left[\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger\right]\psi&=c\left[\partial_x\left(\psi^\dagger\alpha_1\psi\right)+\partial_y\left(\psi^\dagger\alpha_2\psi\right)+\partial_z\left(\psi^\dagger\alpha_3\psi\right)\right] \end{align} \quad{\scriptsize (式27.31)}$
而如果我们定义这样一个向量：
$\small \psi^\dagger\boldsymbol\alpha\psi=\left(\psi^\dagger\alpha_1\psi,\ \psi^\dagger\alpha_2\psi,\ \psi^\dagger\alpha_3\psi\right) \quad{\scriptsize (式27.32)}$
$( \small \psi^\dagger $是1×4矩阵、$ \small \alpha_i $是4×4矩阵、$ \small \psi $是4×1矩阵，于是$ \small \psi^\dagger\alpha_i\psi $就是一个标量，三个凑一块正好是三维向量)
那么，式$27.31$的右边可以看成梯度算子$ \small \boldsymbol \nabla=\left(\partial_x,\partial_y,\partial_z\right) $和$ \small \psi^\dagger\boldsymbol\alpha\psi $的点乘，即：
$\small \begin{align} c\left[\partial_x\left(\psi^\dagger\alpha_1\psi\right)+\partial_y\left(\psi^\dagger\alpha_2\psi\right)+\partial_z\left(\psi^\dagger\alpha_3\psi\right)\right]=c\boldsymbol\nabla\cdot\left(\psi^\dagger\boldsymbol\alpha\psi\right)\ \end{align} \quad{\scriptsize (式27.33)}$
于是守恒流方程就变成了：
$\small \begin{align} \frac{\partial \rho}{\partial t}=-c\boldsymbol\nabla\cdot\left(\psi^\dagger\boldsymbol\alpha\psi\right)\ \end{align} \quad{\scriptsize (式27.34)}$
再对比守恒流的经典物理形式：
$\small \begin{align} \frac{\partial \rho}{\partial t}=-\boldsymbol\nabla\cdot\boldsymbol j \end{align} \quad{\scriptsize (式27.35)}$
我们不难得知，相应的概率流密度为：
$\small \begin{align} \boldsymbol j&=c\left(\psi^\dagger\boldsymbol\alpha\psi\right)\ &=c\left(\psi^\dagger\alpha_1\psi,\ \psi^\dagger\alpha_2\psi,\ \psi^\dagger\alpha_3\psi\right) \end{align} \quad{\scriptsize (式27.36)}$
当然，等式右边括号里这堆符号对我们来说还是很抽象，它有没有物理上更直观的形式？
比如，回想我们在第25课导出的薛定谔方程对应的概率流密度：
$\small \begin{align} \frac{\text i\hbar}{2m}\left(\psi\boldsymbol \nabla \psi^*-\psi^*\boldsymbol \nabla \psi\right)&=\frac{\text i\hbar}{2m}\left[-\frac{2\text i}{\hbar}\boldsymbol p\left(\psi\psi^*\right)\right]=\frac{\boldsymbol p}{m}\rho=\boldsymbol v\rho \end{align} \quad{\scriptsize(式25.30)}$
就是一个速度乘以密度的形式，“流密度”的物理意义跃然纸上，那么我们在式27.36中给出的流密度也能化成这样的形式吗？
答案是“能”，等到我们下节课给出狄拉克方程的一个简单解之后，我们也能推导出一个几乎一模一样的形式来：
$\small \begin{align} \boldsymbol j&=\psi^\dagger\psi\left(\frac{p_x}{m},\frac{p_y}{m},\frac{p_z}{m}\right)\\ &=\rho\left(\frac{p_x}{m},\frac{p_y}{m},\frac{p_z}{m}\right) \end{align} \quad{\scriptsize (式27.37)}$
这样，从物理意义上来说，我们就构造出了概率流守恒定律。
不过我们对于概率流的考察还没完全结束。接下来，我们还要来讨论守恒律的另一个性质：对称性。
在相对论框架下，对称性是一个必须讨论也值得随时把玩的特性。
4) 守恒律的对称性
由于我们是在相对论框架下讨论物理定律，根据相对论的“对称动机”，这个守恒律不仅需要守恒，还需要满足相对论特有的对称性，也就是我们在第24课提到的协变对称性，或者换句话说，这个守恒律应该和参考系无关，在任意参考系下都成立。
而我们在第24课提到过，在不同参考系中，时间和长度、能量和动量等物理量都会发生变化，但是它们组合成的四维向量的模平方是保持不变的，这是一种参考系变化下的对称性。
从另一个角度来讲，这些四维向量的模平方，其实就是四维向量与自身的内积，只不过这种内积的空间部分是负号而已：
$\small \begin{align} P^2&=\left(\frac{E}{c}\right)^2-p_x^2-p_y^2-p_z^2 \\ &=\begin{bmatrix}\frac{E}{c}&-p_x&-p_y&-p_z\end{bmatrix}\begin{bmatrix}\frac{E}{c}\\p_x\\p_y\\p_z\end{bmatrix}\\ \end{align} \quad{\scriptsize (式27.38)}$
而这种内积其实可以推广到任意两个四维向量之间：
$\small \begin{align} \boldsymbol A\cdot \boldsymbol B&=A_tB_t-A_xB_x-A_yB_y-A_zB_z\\ &=\begin{bmatrix}A_t&-A_x&-A_y&-A_z\end{bmatrix}\begin{bmatrix}B_t\\B_x\\B_y\\B_z\end{bmatrix} \end{align} \quad{\scriptsize (式27.39)}$
它们的内积仍然是一个不变量。
现在我们回头来看概率流守恒定律。
我们先把概率流守恒定律的时间部分和空间部分写到一起：
$\small \begin{align} \frac{\partial \rho}{\partial t}+\boldsymbol\nabla\cdot\boldsymbol j=0 \end{align} \quad{\scriptsize (式27.40)}$
接下来，我们把三维梯度扩张一下，变成四维梯度：
$\small \boldsymbol \nabla_4=\left(\frac{\partial }{c\partial t},\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}\right) \quad{\scriptsize (式27.41)}$
(梯度算子的下标4是为了表示这是四维梯度，以区分三维梯度；而时间分量的分母乘以光速$ \small c $是为了量纲统一)
然后把三维流密度也扩张一下，变成四维流密度：
$\small \boldsymbol J=\left(\rho c,j_x,j_y,j_z\right) \quad{\scriptsize (式27.42)}$
那么概率流守恒定律就可以写成内积形式：
$\small \begin{align} 0=\begin{bmatrix}\frac{\partial }{c\partial t}&\frac{\partial }{\partial x}&\frac{\partial }{\partial y}&\frac{\partial }{\partial z}\end{bmatrix}\begin{bmatrix}\rho c\\j_x\\j_y\\j_z\end{bmatrix}=\boldsymbol\nabla_4\cdot\boldsymbol J \end{align} \quad{\scriptsize (式27.43)}$
根据前面的讨论，我们知道，这个内积是一个不变量，在任意参考系下都是0，这也就意味着这个守恒律在任意参考系下都是成立的，这就是一种协变对称性。
不过这里我们要暂停一下，因为有细心的同学已经发现有些地方不对了：
如果我们仔细对比一下式27.39和27.43，会看到，式27.39中，四维向量$ \small \boldsymbol A $的三个空间分量前面有个负号，但是式27.43中的四维梯度三个空间分量却是正的，这是为什么？
简单地说，正负号其实并不是关键，关键的是它们在参考系变换下满足的变换规律。
而这个变换规律，就牵涉到相对论中一对非常重要的概念：协变向量与逆变向量。我们这里先提前预习一下，同学们无法完全理解也没关系，下一章讨论对称性时我们会详细介绍，现在只要模糊知道个大概就行了。
无论是在欧氏空间中的坐标变换，还是不同参考系之间的参考系变换中，如果仔细思考，那么我们都不难发现，普通向量的变换规律其实是和基底的变换规律互逆的。
为了方便理解，我们还是以二维旋转为例来体会一下：
对于一个给定了基底的二维向量空间，如果我们将基底旋转$ \small \theta $角：
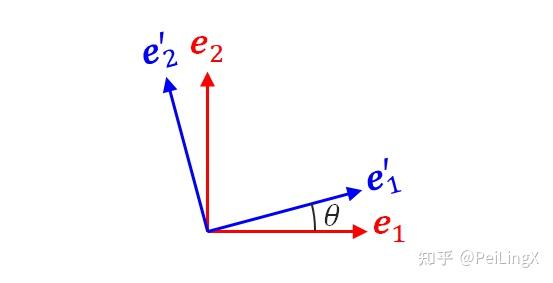
那么新的基底相对于原基底的旋转变换写成矩阵乘法就是：
$\small \begin{bmatrix}\boldsymbol e_1'&\boldsymbol e_2'\end{bmatrix}=\begin{bmatrix}\cos\theta&-\sin\theta\\sin\theta&\cos\theta\end{bmatrix}\begin{bmatrix}\boldsymbol e_1&\boldsymbol e_2\end{bmatrix} \quad{\scriptsize (式27.44)}$
而假设平面上有一个向量$ \small \boldsymbol a $，在原来坐标系下的分量为$ \small \left(a_1,a_2\right)^T $，当基底旋转$ \small \theta $角时，$ \small \boldsymbol a $保持原地不动，其实就相当于相对基底旋转了$ \small -\theta $角
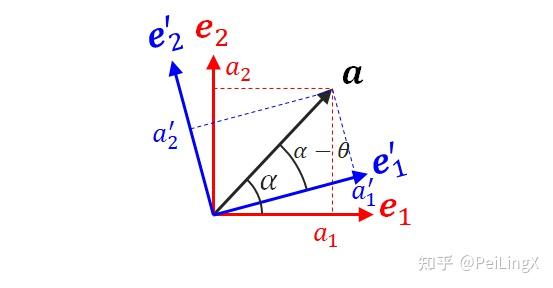
于是它在新的基底下的坐标分量就是：
$\small \begin{bmatrix}a_1'\\a_2'\end{bmatrix}=\begin{bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}\begin{bmatrix}a_1\\a_2\end{bmatrix}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}^{-1}\begin{bmatrix}a_1\\a_2\end{bmatrix} \quad{\scriptsize (式27.45)}$
这个变换正好就是基底变换的逆变换，这种性质我们称为逆变性，相应的向量也称为逆变向量。
那么协变向量是什么呢？我们还是要从内积的不变性说起。
在有的对称变换下，当两个向量做内积的时候，内积的值往往是不随坐标系或参考系变换而改变的(比如四维时空的参考系变换中的内积不变量)。
如果我们将两个向量在原坐标系下的矩阵形式分别抽象地写作$ \small \boldsymbol A,\boldsymbol B $，变换后的矩阵形式写作$ \small \boldsymbol A',\boldsymbol B' $，将基底变换的矩阵写作$ \small \boldsymbol R $，那么内积不变，就意味着：
$\small \boldsymbol A\boldsymbol B=\boldsymbol A' \boldsymbol B' \quad{\scriptsize (式27.46)}$
假设向量$ \small \boldsymbol B $是逆变向量，即$ \small \boldsymbol B'=\boldsymbol R^{-1}\boldsymbol B $，那么上式就可以化为：
$\small \boldsymbol A\boldsymbol B=\boldsymbol A' \boldsymbol R^{-1}\boldsymbol B \quad{\scriptsize (式27.47)}$
等式左右两边要相等，就要求$ \small \boldsymbol A'=\boldsymbol A \boldsymbol R $，也就是向量$ \small \boldsymbol A $满足的是坐标变换的正变换，这样的向量被称为“协变向量”。
实际上，在相对论体系中，每一个向量其实都有协变和逆变两种形式，它们互为对偶。
在三维空间的直角坐标系中，这两者具有相同的形式，所以我们从来没有区分过它，但是相对论中，两者就有区别了。
比如四维动量$ \small \left(\frac{E}{c},p_x,p_y,p_z\right) $是逆变的，它对应的协变动量就是$ \small \left(\frac{E}{c},-p_x,-p_y,-p_z\right) $，两者的内积就是不变量。
在概率流守恒方程中，四维流密度是逆变的，所以我们不过多讨论，我们的重点是要看看四维梯度。
四维梯度是对四维位矢$ \small (ct,x,y,z) $求导所得的向量，而四维位矢本身其实和其他“普通的”四维向量一样是逆变的，但它们对应的四维梯度算子却恰好满足和基底相同的变换规律(我们以后会证明这一点，而且，某种意义下梯度算符其实就可以看成基底本身)，于是$ \small \left(\frac{\partial }{c\partial t},\ \frac{\partial }{\partial x},\ \frac{\partial }{\partial y},\ \frac{\partial }{\partial z}\right) $自身就是一个协变向量(而不需要在空间部分加上负号)。
于是，守恒律就变成了一个典型的协变向量和一个典型的逆变向量之间的内积：
$\small \begin{align} \underbrace{\begin{bmatrix}\frac{\partial }{c\partial t}&\frac{\partial }{\partial x}&\frac{\partial }{\partial y}&\frac{\partial }{\partial z}\end{bmatrix}}_{协变}\underbrace{\begin{bmatrix}\rho c\\j_x\\j_y\\j_z\end{bmatrix}}_{逆变}=\underbrace{0}_{不变} \end{align} \quad{\scriptsize (式27.48)}$
这样一来，概率流守恒定律的确就是两个四维向量的内积了。
当然，我们这里关于协变和逆变的讨论还很粗浅，同学们很难现在就完全理解，不过这没关系，我们以后还会慢慢地通过一些计算规则去熟悉它们，现在我们不妨只笼统地认为：
向量有一协一逆两种形式，而它们的内积在某些变换中，一协一逆两个变换刚好相互抵消，于是得到一个与变换无关的不变量。
到此，我们可以完全相信，我们的确从狄拉克方程出发构造了正确的概率流守恒定律，并且也看到了，重新变回对时间的一阶方程后，我们再次得到了一个正的概率密度(态矢量与自身的内积必然为正数$ )$。
5) 小结与预告
这节课，我们从“对能量开根号得到一阶微分方程”的动机出发，跟随狄拉克的脚步，构造出了一个由4×4矩阵和四分量旋量构成的能量本征方程，也就是狄拉克方程：
$\small \begin{align} \text i\hbar\frac{\partial \psi}{\partial t}&=\left(\alpha_1\hat p_xc+\alpha_2\hat p_yc+\alpha_3\hat p_zc+\beta mc^2\right)\psi\\ &=\begin{bmatrix}mc^2&0&\hat p_zc&\hat p_xc-\text i\hat p_yc\\0&mc^2&\hat p_xc+\text i\hat p_yc&-\hat p_zc\\\hat p_zc&\hat p_xc-\text i\hat p_yc&-mc^2&0\\\hat p_xc+\text i\hat p_yc&-\hat p_zc&0&-mc^2\end{bmatrix}\begin{bmatrix}\psi_1\\\psi_2\\\psi_3\\\psi_4\end{bmatrix} \end{align} \quad{\scriptsize (式27.49)}$
这个方程对我们的意义不仅仅是分量数目的扩张，更重要的是它为我们展现了一个全新的旋量空间，未来我们会慢慢认识到这个空间的玄妙之处。
此外，我们还通过在方程中构造概率密度和概率流密度的传统艺能，证明了这个方程的确解决了负概率的问题，并且还顺便看到了概率流守恒定律在相对论框架下的另一个美妙特质：协变对称性。
不过，我们的重点还是要继续求解狄拉克方程，并且看看它是不是能符合已知的物理事实，同时给我们带来一些新的东西。
下节课我们就来做这件事情。
而这节课结束之前，我们还要来补完前面关于概率流密度的一段证明。
补遗：概率流等式的证明
我们现在来证明前面给出的关于概率流密度的关系式：
$\small \begin{align} \psi^\dagger\left[\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)\right]+\left[\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger\right]\psi&=\partial_x\left(\psi^\dagger\alpha_1\psi\right)+\partial_y\left(\psi^\dagger\alpha_2\psi\right)+\partial_z\left(\psi^\dagger\alpha_3\psi\right) \end{align} \quad{\scriptsize (式27.50)}$
我们先来讨论等式左边的第一项。
首先，为了方便理解，我们将括号中的$ \small \boldsymbol \alpha\psi $展开：
$\small \boldsymbol\alpha\psi=\left(\alpha_1\psi,\ \alpha_2\psi,\ \alpha_3\psi\right) \quad{\scriptsize (式27.51)}$
注意：右边括号里的三个分量分别是三个4×4矩阵乘以4×1的旋量得到的4×1旋量
再作用上梯度算子，就是：
$\small \begin{align} \boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)&=\frac{\partial }{\partial x}\left(\alpha_1\psi\right)+\frac{\partial}{\partial y}\left(\alpha_2\psi\right)+\frac{\partial}{\partial z}\left(\alpha_3\psi\right)\\ &=\alpha_1\frac{\partial \psi}{\partial x}+\alpha_2\frac{\partial \psi}{\partial y}+\alpha_3\frac{\partial \psi}{\partial z}\ \end{align} \quad{\scriptsize (式27.52)}$
注意：这里得到的结果是一个4×1矩阵，写出来就是：
$\small \begin{align} \boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)&= \begin{bmatrix}\partial_z\psi_3+\partial_x\psi_4-\text i\partial_y\psi_4\ \partial_x\psi_3+\text i\partial_y\psi_3-\partial_z\psi_4\\partial_z\psi_1+\partial_x\psi_2-\text i\partial_y\psi_2\\partial_x\psi_1+\text i\partial_y\psi_1-\partial_z\psi_2\end{bmatrix} \end{align} \quad{\scriptsize (式27.53)}$
再左乘$ \small \psi^\dagger $就是：
$\small \begin{align} \psi^\dagger\left[\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)\right]&=\psi^\dagger\frac{\partial }{\partial x}\left(\alpha_1\psi\right)+\psi^\dagger\frac{\partial}{\partial y}\left(\alpha_2\psi\right)+\psi^\dagger\frac{\partial}{\partial z}\left(\alpha_3\psi\right)\ \end{align} \quad{\scriptsize (式27.54)}$
注意：由于$ \small \psi^\dagger $是1×4矩阵，因此乘到$ \small \boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right) ($一个4×1矩阵)的左边后，就得到一个标量。
现在我们来看式27.50左边第二项、也就是厄米共轭项。
重复前面的推导过程，我们将得到：
$\small \begin{align} \boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger&=\frac{\partial }{\partial x}\left(\alpha_1\psi\right)^\dagger+\frac{\partial}{\partial y}\left(\alpha_2\psi\right)^\dagger+\frac{\partial}{\partial z}\left(\alpha_3\psi\right)^\dagger\\ &=\frac{\partial \psi^\dagger}{\partial x}\alpha_1^\dagger+\frac{\partial \psi^\dagger}{\partial y}\alpha_2^\dagger+\frac{\partial \psi^\dagger}{\partial z}\alpha_3^\dagger\ \end{align} \quad{\scriptsize (式27.55)}$
而三个$ \small \alpha_i $的厄米共轭就是它们本身(厄米算符)，于是：
$\small \begin{align} \boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger &=\frac{\partial \psi^\dagger}{\partial x}\alpha_1+\frac{\partial \psi^\dagger}{\partial y}\alpha_2+\frac{\partial \psi^\dagger}{\partial z}\alpha_3\ \end{align} \quad{\scriptsize (式27.56)}$
注意：上式的计算结果是一个1×4矩阵，同学们可以试着写出它的具体分量来。
右乘$ \small \psi $，就是：
$\small \begin{align} \left[\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger\right]\psi &=\frac{\partial \psi^\dagger}{\partial x}\alpha_1\psi+\frac{\partial \psi^\dagger}{\partial y}\alpha_2\psi+\frac{\partial \psi^\dagger}{\partial z}\alpha_3\psi\ \end{align} \quad{\scriptsize (式27.57)}$
注意：这里也是一个1×4矩阵右乘4×1矩阵，得到一个标量。
两式合并，就得到：
$\small \begin{align} \psi^\dagger\left[\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)\right]+\left[\boldsymbol\nabla\cdot\left(\boldsymbol\alpha\psi\right)^\dagger\right]\psi&=\psi^\dagger\frac{\partial }{\partial x}\left(\alpha_1\psi\right)+\psi^\dagger\frac{\partial}{\partial y}\left(\alpha_2\psi\right)+\psi^\dagger\frac{\partial}{\partial z}\left(\alpha_3\psi\right)\\ &\quad+\frac{\partial \psi^\dagger}{\partial x}\alpha_1\psi+\frac{\partial \psi^\dagger}{\partial y}\alpha_2\psi+\frac{\partial \psi^\dagger}{\partial z}\alpha_3\psi\\ &=\frac{\partial}{\partial x}\left(\psi^\dagger\alpha_1\psi\right)+\frac{\partial}{\partial y}\left(\psi^\dagger\alpha_2\psi\right)+\frac{\partial}{\partial z}\left(\psi^\dagger\alpha_3\psi\right) \end{align} \quad{\scriptsize (式27.58)}$
Q.E.D.
参考
- 对于正常的量子力学教材而言，厄米共轭通常会出现在前三章甚至第一章，作者自己都没想到这个系列居然到这里才第一次介绍它
编辑于 2023-10-23 18:26・IP 属地四川