PeiLingX
物理学等2个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》第24课。
了解本系列及本专栏其他文章,请收藏目录:
0) 开篇语
从这节课开始,我们将进入一段新旅程,看看量子力学和狭义相对论结合之后产生的美丽新世界。
由于定态薛定谔方程是能量的本征方程,所以两者的结合点自然是能量关系。
也就是利用相对论能量关系:
$\small E^2=p^2c^2+m^2c^4 \quad{\scriptsize (式23.10)}$
代替牛顿力学的动能关系:
$\small T=\frac{p^2}{2m} \quad{\scriptsize (式8.11)}$
来建立新的能量本征方程。
(为了方便理解和推导,我们暂时不考虑势能项)
不过,在探索新方程之前,我们最好知道一下相对论能量关系是怎么来的,以及它背后有什么样的几何意义。
1) 两个关键词
如果抛开各种具体的物理关系不谈,我们其实可以将狭义相对论简单粗暴地概括成两个关键词:
对称性 + 时空的几何结构
同学们还记不记得中学物理课本提到的狭义相对论的两条基本假设:
第一条:
所有惯性系中,物理定律具有相同形式。
第二条:
所有惯性系中,真空中的光速都相同。
如果我们还记得第22课中对于对称性的定义:物理对象在变换下不变的性质,那么我们马上会意识到,第一条假设说的正好就是一种对称性;
而第二条看起来虽然更像是在描述一个物理现象,但我们其实可以通过它来窥探一个与时空有关的几何原理,后面几节课里与我们形影不离的相对论能量关系,其实都可以看成这个几何原理的延申。
我们这节课里,就主要来体会第二个关键词:时空的几何结构。
对称性在狭义相对论中其实更重要也更美妙,作者也非常努力地尝试过将它也放进这节课里一起展现,但一口气写了五千多字发现还刹不住车的时候,终于还是内心充满挣扎地放弃了,毕竟这部分不太会影响到我们后面的理解。对狭义相对论中物理定律的对称性有兴趣的同学可以读一读费曼的书[1],或者想快速入门的话也可以看看作者另一个系列的前14课。
我们先从回顾相对论时空观的来历开始。
2) 相对论时空观的来历
我们知道,麦克斯韦方程组经过一些简单的解耦运算后,可以得到电磁波的波动方程(也许有同学没见过这个方程具体的形式,但是从麦克斯韦方程种发现电磁波这件事情总是有所耳闻的):
$\small \begin{cases} \frac{\partial^2\boldsymbol E}{\partial x^2}-\frac{1}{\mu_0\epsilon_0}\frac{\partial^2\boldsymbol E}{\partial t^2}=0\ \frac{\partial^2\boldsymbol B}{\partial x^2}-\frac{1}{\mu_0\epsilon_0}\frac{\partial^2\boldsymbol B}{\partial t^2}=0 \end{cases} \quad{\scriptsize (式24.1)}$
(其中,$ \small \mu_0 $为真空中的磁导率,$ \small \epsilon_0 $为真空中的介电常数)
在这个方程中,$ \scriptsize \frac{1}{\mu_0\epsilon_0}=\frac{1}{c^2} $,代表的就是电磁波的波速、也就是光速的平方分之一。
于是两个问题紧接着就来了:
第一问:根据十九世纪物理学的政治正确,波动总是有个传播介质的,那么电磁波的传播介质是个啥?
物理学家们回答:不管它是什么样子,我们先将它叫做“以太”吧。
然后第二问就是:地球在自转和公转,我们在地球上运动方向始终在发生改变,那么我们总有一些运动方向是在相对“以太”运动的,不同方向上的相对运动是否会让我们观测到光速发生变化?
物理学家们又答:当然会,我们做个实验测量一下就知道了。
但他们很快就被(物理意义上的)光速打脸:在接下来的几年里,不同的实验物理学家设计了多个不同的实验方案,最后都测不出任何方向上的光速有任何变化[2]。
但物理学家们仍然不敢相信世界上有可以不依靠介质传播的波,因此他们还是不敢轻易请走“以太”这尊神。
只是几个实验结果摆在那里,总得给个解释吧。
对此,洛仑兹(没错,就是我们上节课提到的那位荷兰物理学家)提出了一种假设:
相对于“以太”运动的物体(这自然就包括了测量仪器)、在运动方向上会发生所谓的洛仑兹收缩,收缩的比例为:
$\small \beta=\sqrt{1-\frac{v^2}{c^2}} \quad{\scriptsize (式24.2)}$
(这可以看成“尺缩效应”的最早版本,虽然它的解释是错误的)
关于如何用洛仑兹收缩解释实验测量不到光速变化,我们这里不展开,有兴趣的同学可以随手找一本狭义相对论教材来看看[3]。
总之,在1905奇迹年之前,物理学界对于“以太”以及“光速不变”的实验结果的态度,就相当于是在说:
“我家里有个妖怪(以太),但是我们永远看不见它(实验测量不到相对于“以太”运动时的光速变化),因为它对我们实施了障眼法(测量仪器相对于“以太”运动时发生了洛仑兹收缩)。”
但常识告诉我们,如果有一个东西,我们没办法通过任何手段直接或者哪怕间接地测量到它,那么我们就应该大胆地认为它不存在。
而且,强行认为“以太”存在,那么“以太”所在的参考系就具有了某种特殊地位,这样会使得使物理定律在不同参考系中产生区别,破坏了我们前面提到的物理定律的对称性。
所以后来的事情我们也都知道了:
爱因斯坦敏锐地捕捉到了问题的关键,也就是对称性问题。他发现,如果去掉“以太”这个永远测量不到的虚无概念,也就去掉了具有特殊地位的“以太”参考系。那么电磁学定律的对称性又会回来,而且还会得到一个更加漂亮的时空体系,也就是相对论时空。
只不过,这个全新的时空观会带来一个非常反直觉的事实:光速在不同参考系中不变,而这个不变性会导致时间和空间尺度在不同参考系中都会发生变化,比如我们中学物理中熟悉的钟慢效应和尺缩效应。
但好在这种反直觉对我们来说其实只是暂时的,如果我们找到了隐藏在这些变化背后的某个不变的时空几何结构,一切就会显得非常自然。
我们接下来就以钟慢效应为例,回顾一下如何从光速不变导出不同参考系中时间尺度的变化,又如何从中挖掘出背后那个神秘的时空几何结构。
3) 钟慢效应
推导钟慢效应的物理情形是这样的:
假设张三站在河岸上静止不动,李四乘船从他面前匀速经过。
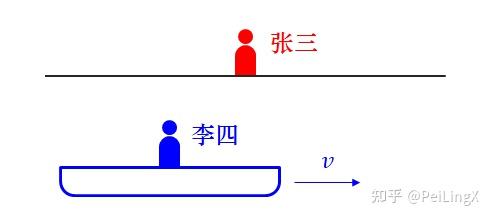
两人交会时,擦出了一团火花、发出耀眼光芒,其中一道光束直奔李四头顶上的一面镜子而去,这面镜子和船体相连,会随着李四一起运动,光打在镜子上,又反射回来,回到李四面前。
现在我们来计算,这道光束从交汇处出发、到回到李四面前这一段旅程所花费的时间。
我们将张三和李四的参考系分别记作$ \small S $系和$ \small S' $系。
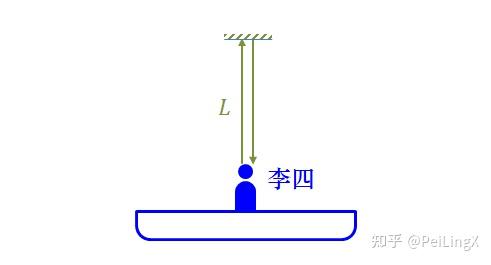
对于李四而言,光束的轨迹就是一来一回两条重合的线段,假设镜子的高度为$ \small L $,那么相应的时间就是:
$\small \Delta t'=\frac{2L}{c} \quad{\scriptsize (式24.3)}$
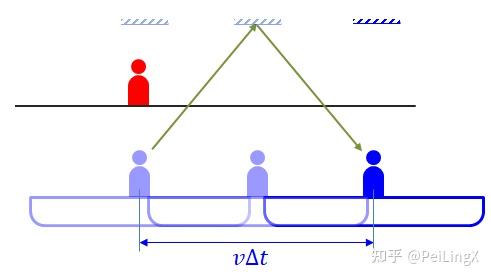
而对于张三而言,假设这道光的传播时间为$ \small \Delta t $,那么由于光束是斜着上去又斜着下来的,两段路程加起来就是$ \small \sqrt{4L^2+v^2\Delta t^2} $,因此运动时间满足一个关于$ \small \Delta t $的简单的二次方程:
$\small \Delta t=\frac{\sqrt{4L^2+v^2\Delta t^2}}{c} \quad{\scriptsize (式24.4)}$
求解后就得到:
$\small \Delta t=\frac{2L}{\sqrt{c^2-v^2}}=\frac{1}{\sqrt{1-v^2/c^2}}\Delta t' \quad{\scriptsize (式24.5)}$
如果我们假设李四随身带了一个钟,用来测量光的传播时间$ \small \Delta t' $,那么我们看到,由于:
$\small \Delta t'=\sqrt{1-v^2/c^2}\Delta t<\Delta t \quad{\scriptsize (式24.6)}$
这看起来就像是李四的钟因为随着船运动而走得更慢了一些,这就是所谓的钟慢效应。
但是敏感的同学会马上发现上面这句话有个问题:
运动是相对的,没有哪个参考系可以被看成绝对静止的参考系,所以相对于李四而言,张三也在运动,为什么不是张三的钟走得更慢一些呢?
为了回答这个问题,我们其实可以假设另一个物理情形:
张三头顶上也有一面镜子,这个镜子固定在岸上,有另外一道光束打到镜子上又返回张三面前,那么这个时候如果我们按照上面的推导思路重新来一遍,就会发现这次两个参考系中光束的传播时间正好反过来,变成了:
$\small \Delta t'=\frac{1}{\sqrt{1-v^2/c^2}}\Delta t \quad{\scriptsize (式24.7)}$
所以,谁的钟走得更慢,根本就不取决于谁在运动(因为这本身就无法区分),而是取决于一些其他的因素。
我们来仔细看一看前面提到的两种情形:在第一种情形中,“光从李四面前出发”和“光回到李四面前”这两件事情,在李四参考系中发生在同一个地点,但在张三参考系中却不是;而第二种情形则正好相反。
这就提示我们:也许同一段过程在某个参考系中的时间间隔和空间间隔有关系?
这其实一点都不奇怪,中学物理课本就曾经告诉过我们:
相对论时空观认为,时间和空间不再相互独立,而是相互联系的一个整体。
现在,我们要来具体看看,它们是通过什么样的几何结构联系到一起的。
4) 时空间隔不变量
我们先忘记四维时空,来考虑一个位于平面上的线段,并且建立一个平面坐标系,然后将线段在两个坐标轴上的投影长度分别记为$ \small \Delta x $和$ \small \Delta y $,那么根据勾股定理,我们知道线段的长度为:
$\small \Delta l^2=\Delta x^2+\Delta y^2 \quad{\scriptsize (式24.8)}$
现在,我们将坐标系旋转某个角度,形成新的坐标系,那么线段在新的坐标轴上的投影会发生变化,但这些改变只是坐标系的变化引起的,线段本身的长度没变,如果我们将新的投影长度记为$ \small \Delta x',\Delta y' $,那么我们仍然有:
$\small \Delta l^2=\Delta {x'}^2+\Delta {y'}^2 \quad{\scriptsize (式24.9)}$
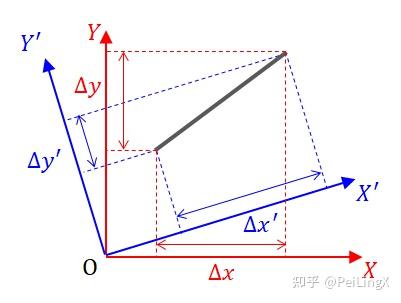
在这里,我们可以很直观地看到,不同坐标系中,$ \small x,y $投影的长度会发生一些此消彼长的变化,但是它们之间可以通过勾股定理联系在一起,并且这种联系对应了一个不随坐标系变化的东西:线段的长度。
我们将这种不随坐标系变化而改变的量称为不变量(Invariant)。
实际上,在四维时空中,我们也可以将不同参考系类比为不同的坐标系,同时将同一段过程在不同参考系中的时间间隔和空间间隔的变化、类比为某个不变量在不同参考系中的“投影”变化。
这样的不变量叫做时空间隔不变量,我们将它记为$ \small \Delta s $,它和它的“投影”(也就是同一段过程在不同参考系中的时间和空间间隔)之间的几何关系长这样[4]:
$\small \Delta s^2=c^2\Delta t^2-\Delta x^2-\Delta y^2-\Delta z^2=c^2\Delta {t'}^2-\Delta {x'}^2-\Delta {y'}^2-\Delta {z'}^2 \quad{\scriptsize (式24.10)}$
也就是说,不同参考系中观察到的时间和空间间隔不同,都是因为这个不变的“长度”$ \small \Delta s $的“投影”在变化。
而我们也可以看到,这个不变量等式和勾股定理还是有一些形似的,两者之间唯一的、也是最本质的区别,就是四维时空的“勾股定理”中、空间项和时间项的正负号正好相反。
有时候我们也会采用另外一种定义:时间项前面是负号、空间项前面是负号,即:
$\small \Delta s^2=-c^2\Delta t^2+\Delta x^2+\Delta y^2+\Delta z^2=-c^2\Delta {t'}^2+\Delta {x'}^2+\Delta {y'}^2+\Delta {z'}^2 \quad{\scriptsize (式24.11)}$
但不管哪种定义,时间项和空间项总是反号的,这也是时间维度不同于空间维度的特殊之处。
现在,有了这个时空间隔不变量关系,我们可以不再借助光速不变原理,而是直接从时空几何的角度出发,用更清晰的几何图像来推导和理解一些物理事实,比如前面提到的钟慢效应。
我们假设,张三站在地面上,李四这次坐着飞行器从张三参考系的空间中的$A$点沿直线匀速飞到了$B$点。
这个过程中,李四在张三参考系中的移动距离为:
$\small \begin{align} \Delta l^2&=\Delta x^2+\Delta y^2+\Delta z^2\\ &=\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2+\left(z_B-z_A\right)^2 \end{align} \quad{\scriptsize (式24.12)}$
而对于李四自己而言,他并没有产生位移,因此他在自身参考系中的移动距离为零:
$\small \Delta {l'}^2=0 \quad{\scriptsize (式24.13)}$
假设这个过程在两个参考系中经历的时间分别为$ \small \Delta t $和$ \small \Delta t' $,那么我们可以利用不变量关系得出:
$\small c^2\Delta {t'}^2=c^2\Delta t^2-\Delta x^2-\Delta y^2-\Delta z^2=c^2\Delta t^2-\Delta l^2 \quad{\scriptsize (式24.14)}$
如果考虑到张三参考系中$ \small \Delta l=v\Delta t ( \small v $为李四相对于张三运动的速率),我们就可以轻松地得出钟慢效应公式。
但导出公式并不是我们现在的重点,我们重点是看看李四经历的时间在这个物理情形下的特殊之处。
我们不难知道,不管是站在地面上的张三、还是正在开车的王二麻子,只要他没有和李四同步运动,那么李四的运动必然在他们的参考系中产生一段距离$ \small \Delta l$
而根据式24.14我们可以看到,时间间隔和空间距离作为不变量的投影,是同时变大或变小的(这和二维平面上线段的两个投影之间此消彼长的关系正好相反),李四参考系中李四移动的距离为零,所以这段运动在其他参考系中持续的时间$ \small \Delta t $就必然大于李四自身经历的时间$ \small \Delta t'$
如果我们假设李四怀里始终抱着一个钟,那么其他任何参考系中的观察者都会看到,李四的时钟走过的时间比他们测到的时间都要短,这就造成了“运动的钟变慢”的结果。
换句话说,当我们考察一个物体的运动所经历的时间时,它自身所在参考系所测得的时间就是所有参考系中“投影”最短的那个。我们将这个最短时间称为固有时(Proper Time),记为$ \small \Delta \tau ( \small \tau $就是希腊字母tau)
它的特殊性将有助于我们接下来推导相对论能量关系。
5) 相对论能量关系
我们知道,在历史上,相对论能量关系是爱因斯坦改造改造牛顿力学时顺手得到的。他的动机也是解决旧的力学定律在新的相对论时空中不对称(不同参考系中不再具有相同形式)的问题,然后在改造过程中导出了新的能量关系。
但我们这里空白太小,没办法把整个相对论力学体系写下来,因此我们决定换一种方式,从前面给出的不变量以及它的“投影”变化的角度出发,用一种更具有几何味道的方法来构造出能量关系。
我们的思路是这样:
考虑一个做惯性运动的物体,那么它会在其他参考系中产生位移,而位移会联系到速度,速度又联系到动量,最后对动量求平方,就是能量了。
只不过,我们现在要构造的位移、速度、动量都是四维化的,它们都有一个共同特点,就是我们刚刚提到的不变量特质,准确地说就是,如果我们将它们都看作四维矢量,那么它们的模平方是不会随着参考系改变的,会改变的只是它们在不同参考系中的“投影”。
我们还是用李四相对于张三运动的例子,假设李四相对于张三运动的位移为:
$\small \Delta \boldsymbol l=(\Delta x,\Delta y,\Delta z) \quad{\scriptsize (式24.15)}$
这个位移只有空间项,现在我们给它加上时间项,构造一个四维位移:
$\small \Delta \boldsymbol s=(c\Delta t,\Delta x,\Delta y,\Delta z) \quad{\scriptsize (式24.16)}$
我们可以看到,这个四维位移的模平方,就是时空间隔不变量:
$\small \Delta s^2=c^2\Delta t^2-\Delta x^2-\Delta y^2-\Delta z^2 \quad{\scriptsize (式24.17)}$
(注意:在相对论语境下,模平方的空间部分是负号,而不再是勾股定理的正号)
现在,如果我们用四维位移除以这段运动所经历的时间,就能构造一个四维速度。
但这里问题来了:同样一段运动在不同参考系中经历的时间不同,我们该选取哪个参考系中的时间呢?
同学们,凭直觉选一个。
没错,我们就选所有参考系里最特殊的那个:固有时$ \small \Delta \tau $,也就是李四本身经历的时间。
(虽然我们暂时也看不出这么选的理由,但先用着吧,后面我们会看到这么选的合理性)
这样,用四维位移除以固有时,我们就构造出了李四的四维速度:
$\small \begin{align} \boldsymbol U=\frac{\Delta \boldsymbol s}{\Delta \tau}=\frac{1}{\Delta \tau}\left(c\Delta t,\Delta x,\Delta y,\Delta z\right) \end{align} \quad{\scriptsize (式24.18)}$
这个四维速度看起来是不是有点“不真实”?它的确不太真实,因为它看起来像是数学上定义出来的,而不是物理上测量出来的,但我们至少可以先出于好奇、找出它和“真实的速度”之间的关系。
考虑到$ \small \Delta t,\Delta x,\Delta y,\Delta z $都是其他任意参考系中测得的时间和位移,我们可以利用它们,算出任意参考系中测得的李四运动的“真实”速度:
$\small \begin{align} \boldsymbol v=\left(v_x,v_y,v_z\right)=\left(\frac{\Delta x}{\Delta t},\frac{\Delta y}{\Delta t},\frac{\Delta z}{\Delta t}\right)\ \end{align} \quad{\scriptsize (式24.19)}$
这个“真实测得的速度”和四维速度之间的关系就是:
$\small \begin{align} \boldsymbol U&=\frac{1}{\Delta \tau}\left(c\Delta t,\Delta x,\Delta y,\Delta z\right)\\ &=\frac{\Delta t}{\Delta \tau}\left(c,\frac{\Delta x}{\Delta t},\frac{\Delta y}{\Delta t},\frac{\Delta z}{\Delta t}\right)\\ &=\frac{\Delta t}{\Delta \tau}\left(c,v_x,v_y,v_z\right) \end{align} \quad{\scriptsize (式24.20)}$
而根据钟慢效应公式,我们又能进一步得到:
$\small \begin{align} \boldsymbol U&=\frac{1}{\sqrt{1-v^2/c^2}}\left(c,v_x,v_y,v_z\right)\ \end{align} \quad{\scriptsize (式24.21)}$
可以看到,四维速度在某个参考系中的空间分量和这个参考系中“观察到的相对速度”之间只差了一个系数$ \scriptsize \frac{1}{\sqrt{1-v^2/c^2}} $,后面我们将这个系数称为洛仑兹因子,并且简单记为$ \small \gamma $,于是:
$\small \begin{align} \boldsymbol U&=\gamma\left(c,v_x,v_y,v_z\right)\ \end{align} \quad{\scriptsize (式24.22)}$
这个关系我们先放着备用。
现在我们继续“不真实的”旅行,来构造四维动量。
速度和动量之间相差一个质量因子,于是我们很自然地就想到了物体的静质量$ \small m ($因为它与参考系无关),用它乘以四维速度,就构造出了四维动量:
$\small \begin{align} \boldsymbol P=m\boldsymbol U=m\frac{\Delta \boldsymbol s}{\Delta \tau}\end{align} \quad{\scriptsize (式24.23)}$
由于四维位移$ \small \Delta \boldsymbol s $的模平方是一个不变量,而四维动量中的$ \small m,\Delta \tau $都是与参考系无关的特定系数,于是我们可以想到,四维动量的模平方也是一个不变量,即:
$\small \begin{align} P^2=\frac{m^2}{\Delta \tau^2}\Delta s^2 \end{align} \quad{\scriptsize (式24.24)}$
但到此为止,我们也只是知道了四维动量有这么一个不变量的几何特质而已,这个四维动量对我们来说仍然像是一个生硬的数学定义,而缺乏具体的物理含义,或者说“不真实”。
所以接下来我们就要来回答两个重要问题:
这个不变量$ \small P^2 $等于什么?它的物理意义又是什么?
为了回答第一个问题,我们不妨先利用式24.22中的关系,将四维动量写成这样的形式:
$\small \begin{align} \boldsymbol P=m\boldsymbol U=\gamma m\left(c,v_x,v_y,v_z\right) \end{align} \quad{\scriptsize (式24.25)}$
然后对它取模平方:
$\small \begin{align} P^2=\frac{m^2}{1-v^2/c^2}\left(c^2-v^2\right)=m^2c^2 \end{align} \quad{\scriptsize (式24.26)}$
这样,我们就得到了四维动量不变量的具体值。
接下来,我们来看看它的物理意义。
不知道同学们在式24.25中有没有注意到一个似曾相识的东西:
$\small m'=\gamma m=\frac{m}{\sqrt{1-v^2/c^2}} \quad{\scriptsize (式24.27)}$
没错,这就是我们熟悉的所谓的动质量!
如果将它乘入四维动量的各个分量中,我们会得到:
$\small \begin{align} \boldsymbol P=\left(\gamma mc,\gamma mv_x,\gamma mv_y,\gamma mv_z\right) \end{align} \quad{\scriptsize (式24.28)}$
它的空间分量$ \small \left(\gamma mv_x,\gamma mv_y,\gamma mv_z\right) $,就是我们在某个参考系下“真实测得的”动量$ \small \boldsymbol p $,它相对于牛顿力学中的动量正好多了一个洛仑兹因子$ \small \gamma $,这也是我们所熟悉的物理事实。
如果说前面对于四维位移和四维速度的构造还只是某种意义上的数学游戏的话,那现在的四维动量就终于具有明确的物理意义了,而这也说明了我们前面看似没头没脑的构造其实是合理的。
需要注意的是,四维动量里的 $\small \gamma$ 其实是在推导四维速度的时候出现的,因此它应该被看成对四维速度的修正而不是对质量的修正。但由于我们实际测量到的速度还是 $\small \left(v_x,v_y,v_z\right)$ ,因此 $\small \gamma$ 看起来就像是质量在变化,这才有了“动质量”的概念。
所以严格来说“动质量”的提法并不是太合适,不过这些只是概念上的问题,并不影响物理本质。
接下来,我们将$ \small P^2 $也分解成时间部分和空间部分:
$\small m^2c^2=P^2={m'}^2c^2-p^2 \quad{\scriptsize (式24.29)}$
然后再在两边乘上光速平方,得到:
$\small m^2c^4={m'}^2c^4-p^2c^2 \quad{\scriptsize (式24.30)}$
是不是有点我们熟悉的味道了?
根据质能关系,我们知道,这个式子的左边就是物体的静能量,右边第一项是物体的总能量,第二项某种意义上可以看作动能项(差了一个质量因子)
而它的物理意义、或者说“几何”意义也就出来了:
- 静能量$\small m^2c^4 $可以看作四维动量模平方不变量;
- 总能量$\small {m'}^2c^4 $可以看作静能量在时间维度上的“投影”;
- 动能项$\small p^2c^2 $可以看作静能量在空间维度上的“投影”。
而如果将空间“投影”部分移到等式另一边,我们就得到:
$\small \begin{align} m'^2c^4&=p^2c^2+m^2c^4\end{align} \quad{\scriptsize (式24.31)}$
再令$ \small m'^2c^4=E^2 $,我们就得到了那个熟悉的能量关系:
$\small E^2=p^2c^2+m^2c^4 \quad{\scriptsize (式23.10)}$
到此为止,这个式子在我们眼里终于不再是一堆来历不明的物理关系,而变成了一组虽然抽象但图像清晰的“几何投影”关系。
6) 总结与预告
这节课里,我们从几何的视角,一步步导出了相对论能量关系,并且看到了它对应的几何图景。
我们先从熟悉的光速不变原理出发,回顾了钟慢效应的导出过程,并且在其中发现,一段运动过程在不同参考系中经历的时间和走过的距离相互关联。
接下来,我们用平面上的勾股定理做类比,导出了时间和距离之间的定量联系,它们对应着一个时空间隔不变量关系:
$\small \Delta s^2=c^2\Delta t^2-\Delta x^2-\Delta y^2-\Delta z^2=c^2\Delta {t'}^2-\Delta {x'}^2-\Delta {y'}^2-\Delta {z'}^2 \quad{\scriptsize (式24.10)}$
这个关系告诉我们,一段运动过程在各个空间中所经历的时间和空间间隔的不同,其实可以看成一个时空间隔不变量的“投影”的变化,就像一个线段在平面上不同坐标系中的投影变化一样。
有了这样的几何图景,我们继续往下延伸,将时空距离不变量看成一个运动物体的四维时空位移的模平方,然后引申出四维位移,并且通过它构造了四维速度和四维动量:
$\small \boldsymbol U=\frac{\Delta \boldsymbol s}{\Delta \tau}=\frac{1}{\Delta \tau}\left(c\Delta t,\Delta x,\Delta y,\Delta z\right) \quad{\scriptsize (式24.32)}$
$\small \boldsymbol P=\frac{m}{\Delta \tau}\Delta \boldsymbol s=\frac{m}{\Delta \tau}\left(c\Delta t,\Delta x,\Delta y,\Delta z\right) \quad{\scriptsize (式24.33)}$
然后我们看到,四维动量的模平方也是一个不变量,我们经过一段简单的推导,发现这个不变量为:
$\small P^2=m^2c^2 \quad{\scriptsize (式24.27)}$
而在推导过程中,我们还发现,这个不变量可以拆解为时间维度上的“投影”和空间维度上的“投影”:
$\small m^2c^2={m'}^2c^2-p^2 \quad{\scriptsize (式24.29)}$
如果在两边同时乘以光速平方$ \small c^2 $:
$\small m^2c^4={m'}^2c^4-p^2c^2=E^2-p^2c^2 \quad{\scriptsize (式24.34)}$
再结合质能关系,我们就发现,这个不变量对应的是运动物体的静能量,而它在不同参考系中的“时间投影”,对应的是物体在该参考系中的总能量,“空间投影”对应的是该参考系中的动能项。
而如果将$ \small p^2c^2 $移到等式的另一边,我们就得到了相对论能量关系:
$\small E^2=m^2c^4+p^2c^2 \quad{\scriptsize (式23.10)}$
而现在我们可以透过不明所以的物理关系的表象,看到其中各种能量之间的“几何投影关系”的本质。
顺便说一句,刚才提到的这些不变量性质,其实也可以看成是相对论时空中对称性的一个体现,毕竟它是某些物理量在参考系变换下保持不变,这完全符合我们对于对称性的理解。
而这个不变量的对称性,和我们前面提到但未介绍的各个物理定律的对称性,其实都是所谓“相对论协变对称性”的一种(在相对论中,它们都可以写成某种形式简洁的张量方程)。这种“协变对称性”是相对论中的基本审美情趣,并且也将影响到我们对能量本征方程的处理。
带着这种审美,我们就要来尝试着构造符合相对论协变对称性的能量本征方程了。
参考
- 《费曼讲物理:相对论》
- 有兴趣了解的同学可以翻阅《狭义相对论(第二版)》,刘辽 著,P. 6 ~ P. 12
- 比如《狭义相对论(第二版)》,刘辽 著,P. 12
