PeiLingX
物理学等 2 个话题下的优秀答主

---

本文是深度科普系列《从线性代数到量子力学》第21课。

本系列及本专栏其他文章，建议收藏目录：

专栏文章总目录

---

0) 前情提要

上节课里，我们首先梳理了整个氢原子薛定谔方程的求解思路：分化瓦解、逐个击破。

我们根据$\small \hat H,\hat L^2,\hat L_z$具有共同本征态的特点、以及各个偏导数与算符的球坐标表象之间的关系，可以将方程化为分别与$\small \varphi,\theta,r$有关的三个层层嵌套的常微分方程，求解它们，我们就可以分别得到方程解中关于$\small \varphi,\theta,r$的部分。

而在这个过程中我们看到，整个方程的解正好就是三个部分的乘积：

$\small \psi(r,\theta,\varphi)=R(r)\varTheta(\theta)\varPhi(\varphi) \quad{\scriptsize (式20.14)}$

而我们在上节课已经找出了角向的两个解$\small \varTheta(\theta)$和$\small \varPhi(\varphi)$，以及相应的角动量本征值，这节课，我们就来解决剩下的径向解，完成整个方程解的最后一块拼图，然后我们会简单体验一下方程解的一些物理意义。

---

1) 氢原子方程的径向解

上节课我们提到，薛定谔方程可以分解为径向和角向两部分：

$\small \begin{align} E\left|\psi\right>&=\left(\frac{1}{2m_e}\hat p_r^2+\hat V\right)\left|\psi\right>+\frac{1}{2m_er^2}\hat L^2\left|\psi\right> \end{align} \quad{\scriptsize (式20.1)}$

如果我们将$\small \hat L^2$的本征值$\small \lambda$ (式20.10右边)作为已知条件代入总的薛定谔方程中，就能消去所有与$\small \theta,\varphi$有关的项(因为它们都包含在角动量平方算符内)。

再将动量算符还原到球坐标表象下，那么我们就能将整个方程化为：

$\small -\frac{\hbar^2}{2m_e}\left[\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial }{\partial r}\right)+\frac{\lambda}{r^2}\right]\psi+V(r)\psi=E\psi \quad{\scriptsize (式20.13)}$

而上节课我们已经求得，角动量平方的本征值为：

$\small \lambda=l(l+1)\hbar^2 \quad{\scriptsize (式20.27)}$

将它代入总的薛定谔方程中，就得到：

$\small -\frac{\hbar^2}{2m_e}\left[\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial }{\partial r}\right)+\frac{l(l+1)}{r^2}\right]\psi+V(r)\psi=E\psi \quad{\scriptsize (式21.1)}$

这个方程的解和势函数的具体形式有关，我们将氢原子的库仑势代入，就得到：

$\small -\frac{\hbar^2}{2m_e}\left[\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial }{\partial r}\right)+\frac{l(l+1)}{r^2}\right]\psi-\frac{1}{4\pi\epsilon_0}\frac{e^2}{r}\psi=E\psi \quad{\scriptsize (式21.2)}$

再考虑到分离变量函数$\small \psi=R(r)\varTheta(\theta)\varPhi(\varphi)$中，$\small \varTheta(\theta),\varPhi(\varphi)$都和$\small r$无关，可以作为系数左右约掉，于是方程就正式变成了$\small R(r)$的常微分方程：

$\small -\frac{\hbar^2}{2m_e}\left[\frac{1}{r^2}\frac{\text d }{\text d r}\left(r^2\frac{\text d }{\text d r}\right)+\frac{l(l+1)}{r^2}\right]R(r)-\frac{1}{4\pi\epsilon_0}\frac{e^2}{r}R(r)=ER(r) \quad{\scriptsize (式21.3)}$

这个方程看起来也不太友好，但仍然是可以求解的，只是求解过程更加繁琐一些，我们依然省略求解过程直接给出答案[1]：

$\small R(r)$的解具有这样的形式：

$\small R_{nl}(r)=N_{nl}\cdot r^l\cdot \exp\left({-\frac{1}{n}\frac{r}{\rho_B}}\right)\cdot \text F\left(-n+l+1,2l+2,\frac{2}{n}\frac{r}{\rho_B}\right) \quad{\scriptsize (式21.4)}$

这个式子里出现了很多陌生的符号和函数，我们一个个来解释：

• 序号$\small n$称作“主量子数”，它是整个能量本征值的序号(也就是玻尔能级的序号)，我们等一下再讨论它；
• $\small N_{nl}$是归一化系数(以使整个本征函数在全空间的概率积分等于1)，展开写就是：

$\small N_{nl}=\left(\frac{2}{n\rho_B}\right)^l\cdot\sqrt{\frac{1}{\rho_B^3}\frac{(n+l)!}{(n-l-1)!}}\cdot\frac{2}{n^2(2l+1)!} \quad{\scriptsize (式21.5)}$

• $\small \rho_B=\scriptsize \frac{4\pi\epsilon_0\hbar^2}{m_e e^2}$，称为玻尔半径，是一个具有长度量纲的常数，大小约为$\small 0.53\ \text{A}$，我们在玻尔能级公式里其实看到过这个因子，它经常作为一个整体出现，并且尺度也和氢原子基态电子“轨道半径”相当，因此我们将它单独作为一个常数；
• 出现在公式最后那一项的函数$\small \text F$叫做合流超几何函数(Confluent Hypergeometric Function)，它是这样一个幂级数：

$\small \text F(a,b,x)=\sum_{k=0}^{\infty}{C_k\frac{x^k}{k!}} \quad{\scriptsize (式21.6)}$

其中系数$\small C_k$由下面的递推式给出：

$\small \left\{\begin{align} &C_{k+1}=\frac{a+k}{b+k}C_k\\ &C_0=1 \end{align}\right. \quad{\scriptsize (式21.7)}$

展开写就是：

$\small \text F(a,b,x)=1+\frac{a}{b}x+\frac{a(a+1)}{b(b+1)}\frac{x^2}{2!}+\frac{a(a+1)(a+2)}{b(b+1)(b+2)}\frac{x^3}{3!}+\cdots \quad{\scriptsize (式21.8)}$

而如果将径向本征函数解和角向解合并到一起，我们就得到了整个能量本征函数：

$\small \psi_{nlm}(r,\theta,\varphi)=R_{nl}(r)Y_{lm}(\theta,\varphi) \quad{\scriptsize (式21.9)}$

下面我们来看看各个本征函数对应的能量本征值。

---

2) 能量本征值与能级简并

在我们上面求解的关于$\small r$的微分方程中，其实已经包含了构成总能量的所有项(只不过径向组仍然以算符形式存在，而角向组已经化成了本征值)，因此求解这个方程得到的本征值也就是电子的能量本征值了。

毫无意外地，这个能量本征值就是玻尔能级公式(这也是为什么当年薛定谔方程一出场就惊艳了整个物理世界)：

$\small E_n=-\frac{1}{n^2}\frac{m_e e^4}{8h^2\varepsilon_0^2} \quad {\scriptsize(式16.20)}$

但是等一等，如果仔细思考一下，我们会发现一个问题：

能量本征函数$\small \psi_{nlm}$对应着三个量子数$\small n,l,m$，而这里得到的能量本征值只与$\small n$有关，与$\small l,m$无关，这就意味着，同样的能级$\small E_n$可能对应着不同的$\small l,m$，也就是说，能级$\small E_n$是简并的。

我们先来算一算它的简并度，然后简单聊一聊这背后的物理意义。

由于$\small m$的信息是隐藏在$\small l$当中的(对应着$\small L^2$的简并)，因此计算能级简并度时，我们其实只需要知道：

一个$\small n$最多可以对应多少个$\small l$？

这个问题的答案，还是要回到本征函数的径向解中去寻找，具体地说，我们要从径向解的收敛性说起。

在这里，我们将省略详细的计算[2]，只定性地介绍这个思路。

我们首先注意到，径向解中出现的合流超几何函数和指数函数$\small e^x$的泰勒展开有点像(就多了个系数)，并且，很容易看出，随着$\small x\rightarrow \infty$，这个函数是发散的。

而在径向解$\small R_{nl}$中，虽然$\small \text F\scriptsize\left(-n+l+1,2l+2,\frac{2}{n}\frac{r}{\rho_B}\right)$前面乘了一个衰减的指数因子$\small \exp\scriptsize\left({-\frac{1}{n}\frac{r}{\rho_B}}\right)$，但即使是这样，如果$\small \text F$是一个最高次数没有限制的无穷级数，最终的乘积在$\small r\rightarrow\infty$时仍然是发散的[3]。

而我们在第10课的讨论中曾经提到过，束缚态的能量本征函数在无穷远处是收敛的(也就是粒子出现在无穷远处的概率为0)。

从数学上来说，这就要求我们通过某些限制条件，将$\small \text F$截断成一个有限的多项式，这样，当它乘以一个衰减的指数因子时，整个径向函数才能在无穷远处收敛。

具体怎么做呢？

我们看到，合流超几何函数中，第$\small k$项的系数为：

$\small C_{k}=\frac{a(a+1)\cdots\left(a+k-1\right)}{b(b+1)\cdots\left(b+k-1\right)} \quad{\scriptsize (式21.10)}$

如果$\small a$是$0$或某个负整数，比如我们记$\small a=-n_r ( \small n_r=0,1,2\cdots )$，那么当$\small k-1=n_r$的时候，$\small C_k$以及更高次项系数的分子中，都会出现$\small a+k-1=-n_r+n_r=0$的因子，这将使$\small C_k$以及更高次项的系数全部变成$0$。

这样，合流超几何函数就变成了一个只有$\small n_r$项的有限多项式，如果再乘上衰减因子$\scriptsize \exp\scriptsize\left({-\frac{1}{n}\frac{r}{\rho_B}}\right)$，就会随着$\small x\rightarrow \infty$收敛到$0$，这也就使得径向函数具有了束缚态的意义。

回到$\small \text F\scriptsize\left(-n+l+1,2l+2,\frac{2}{n}\frac{r}{\rho_B}\right)$中，就对应着：

$\small -n+l+1=-n_r\ \Rightarrow\ n_r=n-l-1 \quad{\scriptsize (式21.11)}$

这里定义的$\small n_r$称为“径向量子数”，我们可以用它重新将合流超几何函数写为：

$\small \text F\scriptsize\left(-n+l+1,2l+2,\frac{2}{n}\frac{r}{\rho_B}\right) \ \rightarrow\ \text F\scriptsize\left(-n_r,2l+2,\frac{2}{n}\frac{r}{\rho_B}\right) \quad{\scriptsize (式21.12)}$

现在我们来看角量子数的取值范围。

根据上面的等式关系，我们可以知道：

$\small l=n-n_r-1 \quad{\scriptsize (式21.13)}$

由于$\small n_r\geq 0$，因此角量子数的取值范围就是：

$\small l=0,1,2,\cdots,n-1$

于是，同一个能级$\small E_n$就包含着$\small n-1$重的角量子数。而再考虑到一个角量子数$\small l$中还包含了$\small 2l+1$个磁量子数，因此整个能级$\small E_n$的简并度就是：

$\small D_n=\sum_{l=0}^{n-1}\left(2l+1\right)=n^2 \quad{\scriptsize (式21.14)}$

读到这里，也许有同学会好奇，这个简并背后的物理意义是什么？

首先，我们需要知道的是，其实并不是所有的球对称势场中都存在能级简并。比如我们现在讨论的简并，其实就只会出现在形如$\small V(r)=\scriptsize-\frac{k}{r}$的势函数中。

粗略地看起来，总能量的简并只是意味着某些径向能量值与角向能量值的组合恰好相等，这似乎只是$\small V(r)=\scriptsize-\frac{k}{r}$这样的势函数导致的巧合而已。

但其实这个简并背后蕴含着更深层次的物理图景。

所谓更深层次的物理图景，与一个名叫拉普拉斯-龙格-楞次矢量(Laplace-Runge-Lenz Vector, LRL Vector)的守恒量有关，具体等我们未来正式讨论对称性的时候再来介绍[4]。

在本节课的最后，我们要来解决第16课曾经提到过的玻尔模型的缺陷：无法解释为什么氢原子核外电子不会从基态继续跌落到原子核中。

---

3) 永不跌落的电子

所谓“核外电子不会跌落到原子核中”，在量子力学中，其实就意味着一件事情：电子出现在原子核附近的概率为0，所以接下来的事情也很简单：只要我们能通过电子的波函数来算出这个概率就完事儿了。

我们以基态波函数为例来算一算。

基态意味着电子的主量子数为最小值1，而角量子数和磁量子数都是0，即：

$\small n=1,\ l=m=0$

将$\small l,m$代入上节课的式20.24和式20.25，我们可以得到这个本征态对应的角向解为：

$\small Y_{00}(\theta,\varphi)=\sqrt{\frac{1}{4\pi}} \quad{\scriptsize (式21.15)}$

而将$\small n,l$代入式21.4，可得径向解为：

$\small R_{10}(r)=\frac{2}{\sqrt{\rho_B^3}}\exp{\left(-\frac{r}{\rho_B}\right)} \quad{\scriptsize (式21.16)}$

于是波函数为：

$\small \psi_{100}=\frac{1}{\sqrt{\pi\rho_B^3}}\exp\left(-\frac{r}{\rho_B}\right) \quad{\scriptsize (式21.17)}$

于是相应的概率密度就是：

$\small \left|\psi_{100}\right|^2=\frac{1}{\pi\rho_B^3}\exp\left(-\frac{2r}{\rho_B}\right) \quad{\scriptsize (式21.18)}$

算到这一步，同学们是不是发现事情有点不对劲：

当$\small r=0$时，这个概率密度居然不是$0$，而是$\small \frac{1}{\pi\rho_B^3}$，这是不是意味着电子出现在原子核处的概率不是0 (而且这个位置还是概率密度的最大值)？

别急，我们来认真理一理“电子出现在某处的概率”这个表述的真实含义：

由于氢原子模型是球对称的，因此当我们讨论电子出现在“某处”时，其实应该理解为电子出现在半径为某个$\small r$附近的概率。

而“半径某个$\small r$附近”可以理解为一个球壳，它与原子核的距离为$\small r$、厚度为$\small \text dr$

而电子出现在这个球壳中的概率就是：

$\small \text dP=\left|\psi_{100}\right|^2\cdot 4\pi r^2\text dr=4\left(\frac{r}{\rho_B}\right)^2\exp\left(-2\frac{r}{\rho_B}\right)\text d\left(\frac{r}{\rho_B}\right) \quad{\scriptsize (式21.19)}$

我们可以求出它对半径$\small r$的概率密度分布函数：

$\small f(r)=\frac{\text dP}{\text dr}=\frac{4}{\rho_B}\left(\frac{r}{\rho_B}\right)^2\exp\left(-2\frac{r}{\rho_B}\right)\quad{\scriptsize (式21.20)}$

可以看出，当$\small r=0$时，$\small f(0)=0$，也就是电子出现在原子核附近的概率为0

(可以看出，只要概率密度函数不是$2$阶以上的无穷大，这个概率密度就必然会在$\small r\rightarrow 0$时收敛)

这就让我们相信，电子不会坠落到原子核中，因此我们身边的世界是稳定的。

不过，推导到这里，我们还可以再进一步，顺手完成另一件事情。

如果我们将$\small f(r)$的图画出来：

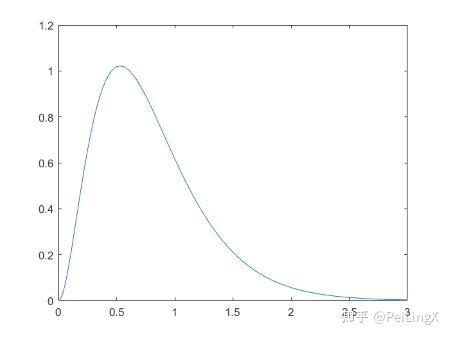
横坐标为电子到原子核的距离$($单位：埃)

我们会发现，电子出现概率最大的地方是在$\small r=\rho_B=0.53\ \text{A}$处、也就是玻尔半径附近的球壳里，这也就与玻尔的原子模型对上号了。

(关于这个极值点的数学证明也很简单，同学们自己试一下吧)

这样，我们就看到，通过求解氢原子方程，我们能得到玻尔模型所能得出的结论，也能解释玻尔模型不能解释的事情，这也是为什么薛定谔方程一面世就惊艳四座。

---

4) 总结与预告

这节课，我们完成了求解氢原子薛定谔方程的后半部分，得到了方程的径向解，并且顺手解释了玻尔氢原子模型所不能解释的问题：为什么电子不会坠落到原子核中。

而在求解过程中，我们发现，对于库仑势这种特殊的势场而言，电子的能级也存在着一种简并，这种简并看起来只是因为某些径向能量值与角向能量值的组合恰好相等，似乎是一种偶然的结果，但其实它的背后也蕴含着一种不那么明显的对称性。

关于这种对称性，我们放到以后再来介绍，而在下节课里，我们要先回到角向解，来体验一个物理图景相对比较直观的角向解的对称性。

我们在第18课中曾经提到：由于球坐标的定义问题，$\small z$轴方向看起来要比其他方向更特殊一些，这会导致薛定谔方程的本征函数解也会展现出围绕$\small z$轴的中心对称性(我们下节课会展示这一点)、但对于其他方向(比如$\small x,y$方向)而言却并不对称，这使得解的球对称性看起来像是被破坏了。

但另一方面，在物理上我们凭直觉都能知道，球对称势下方程的解不应该存在任何方向上的不对称。

那么这种矛盾怎么解决呢？我们下节课就来聊一聊。

参考

1. 求解过程仍然是几乎所有量子力学教材上都会记载，作者读过的书里感觉交待得比较清楚的是卢文发的《量子力学与统计力学》。
2. 详细计算可参考钱伯初《量子力学》第181~182页
3. 仍然推荐参考钱伯初《量子力学》第181~182页
4. 想提前了解的同学，可以阅读樱井纯《现代量子力学(第2版)》中译本第194~198页的内容，不过这个矢量的物理图景以及背后的对称性都非常隐匿和抽象，即使看了书，我们也很难对它形成一个直观认识，所以如果看完觉得没看懂，不要怀疑自己，也不要责怪教材，这就不是一个能直观理解的对象。

编辑于 2022-06-08 12:19