PeiLingX
物理学等2个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》的第11课。
了解本系列及本专栏其他文章,请收藏目录:
0) 开篇语
在本系列第4课和第5课中,我们已经通过通过对斯特恩-盖拉赫实验的介绍,初次体会了电子在两个相互垂直的方向上的自旋之间的不确定性关系。
但这毕竟是还一个远离经典物理的例子,从本课开始,我们将关注一对非常典型的经典力学量:位置和动量。
我们将在它们身上更仔细地体验不确定性原理以及背后的线性代数的影子,并且最终导出那个我们见到过无数次、却不明所以的海森堡不确定性关系(考虑一维情形):
ΔxΔpx≥ℏ2(式11.1)
而为了对这个式子预先有个直观体验,我们将借(Chao)鉴(Xi)顾樵先生的例子,从电子的单缝衍射实验说起。
1) 单缝衍射
在中学物理中我们知道,做光子或电子的单缝衍射实验时,有这样一个定性结论:
狭缝的宽度Δx越窄,衍射范围越宽(这里指的是“中央主极大衍射范围”、也就是中央那个最大的衍射峰的宽度,如下图),这个范围通常用中央一级衍射角θ来表征:
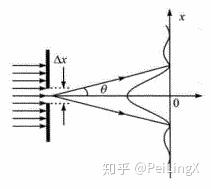
暂借顾樵版《量子力学II》配图,稍后自己画图更换
而上述关系可以描述为:
sinθ=λΔx(式11.2)
(其中 λ 为波长)
在这里,我们首先可以很容易想到,狭缝的宽度Δx可以表征通过狭缝的粒子在x方向上的位置的不确定度。
那么剩下另一个问题就是:一级衍射角θ意味着什么?
我们从一个半经典的分析中寻找答案:
如果我们假设电子的动量大小为p,并且假设电子从狭缝到衍射屏之间沿直线前进(虽然“电子路径”并不存在),那么到达主极大衍射范围上下两个边界的电子在x方向的动量分量分别为psinθ和−psinθ
如果只考虑中央衍射峰,这就意味着电子在x方向上动量的不确定度与衍射角相当:
Δpx∼2psinθ(式11.3)
(这里并不是严格的相等关系,因此用~代替等号)
代入式11.2,可知:
ΔxΔpx∼2pλ(式11.4)
而根据德布罗意关系:
p=hλ(式9.8)
我们就能得到一个半定性半定量的关系式:
ΔxΔpx∼2h(式11.5)
这就隐约有点海森堡那个不确定性关系式的风貌了。
而在这个实验背景下,这个关系式的物理意义也非常明确:
狭缝越窄、即通过狭缝的电子的x坐标越精确,它的动量分量px就会变得越不确定,衍射范围也就越宽。
虽然这里的不确定度还只是一种定性描述,但通过这段分析,我们从电子衍射宽度的简单规律中,的确体会到了一个粒子的位置坐标与它在同一方向上的动量分量之间的不确定关系。
有了这个可以确信的物理事实,我们就能安心地去追究它背后的数学根源,而不会觉得一切都是纯数学世界里的空中楼阁。
后面的课程里,我们就要来看看,如何从数学原理上理解这个物理事实的必然性。
不过在此之前,我们要先对“不确定度”Δx,Δpx的真正含义做一个说明。
2) 不确定度
我们首先假设,有个粒子处于某个状态|ψ⟩,并且这个|ψ⟩不是位置的本征态,也不是动量的本征态,那么当我们去测量它的位置或动量时时,测量结果必然是随机的。
而假如我们有大量处于状态|ψ⟩的粒子、并且逐个测量这些粒子的位置或动量时,我们自然会得到不同的测量结果,而这些测量结果的波动可以用标准差来衡量,而这就是不确定度Δx,Δpx的意义。
这里不难想到的是,状态|ψ⟩不同,测量结果的标准差也不同。
比如处在某个位置本征态的粒子,位置的标准差必然是0,而动量的标准差是无穷大;反过来,处于某个动量本征态的粒子,位置的标准差是无穷大,而动量的标准差是0.
所以,证明不确定性关系式的关键,就是要计算不同状态下,位置和动量两个标准差的“联动关系”。
到了这一步,看起来我们的画风已经转向了概率计算问题,与本系列的幕后大佬线性代数似乎没啥关系了。
但实际上,位置标准差和动量标准差之间的“联动关系”背后,仍然能看到线性代数的影子。
还记得我们在第8课提到的“表象”吗?
我们当时提到过,表象其实就是线性代数中的基底的量子版本,当我们用位置的本征态作为基底来表示态矢量的时候,得到的就是它的位置表象,用动量的本征态作为基底表示态矢量的时候,得到的就是它的动量表象。
而如果我们能像线性代数中的基底变换一样,找到位置表象和动量表象之间的表象变换关系,我们就能计算某个状态下这两者的标准差的联动关系了。
所以这个问题归根结底还是逃不出线性代数的掌心。

为了简单体会一下表象变换,我们再来回顾一遍第5课中的级联斯特恩-盖拉赫实验。
3) 回顾:级联斯特恩-盖拉赫实验
在第5课关于级联斯特恩-盖拉赫实验的讨论中,我们知道:
电子在某个方向、比如z方向上的自旋处于确定状态(+z方向或−z方向)时,在其他方向上、比如y方向上的自旋就处于不确定状态。
我们从态矢量的观点解释了这个现象:z方向自旋(记为Sz )的两个本征态|z+⟩,|z−⟩与y方向自旋Sy的本征态|y+⟩,|y−⟩并不“重合”,而是它们的线性组合:
{|z+⟩=1√2|y+⟩+1√2|y−⟩|z−⟩=−1√2|y+⟩+1√2|y−⟩(式11.6)
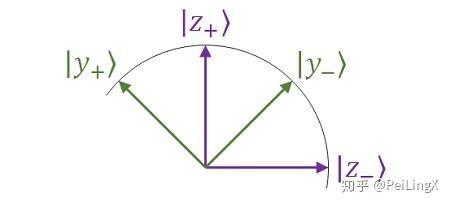
任意一个状态|ψ⟩,我们假设,以z方向自旋(记为Sz )的两个本征态|z+⟩,|z−⟩为基底时,它的表达式为:
|ψ⟩=a1|z+⟩+a2|z−⟩(式11.7)
那么ψz=(a1,a2)T就是这个态矢量|ψ⟩的“z自旋表象”
而如果将前面的|z+⟩,|z−⟩与|y+⟩,|y−⟩的变换关系代入“z自旋表象”下|ψ⟩的表达式,我们又能得到|ψ⟩的“y自旋表象”,即:
ψy=1√2(a1−a2,a1+a2)T=[1√2−1√21√21√2][a1a2]=[1√2−1√21√21√2]ψz(式11.8)
这样,我们找到了Sz和Sy两种自旋表象下的表象变换关系,即矩阵[1√2−1√21√21√2]
对于在线性代数中身经百战的同学们而言,这个变换理解起来并不会有什么困难。
而坐标表象和动量表象之间的转换,也就仅仅是计算更复杂一点、将上面的变换从2维情形推广到“无穷维”情形而已。
下节课,我们就来梳理这个问题。
4) 总结与预告
在这节课短短的篇幅里,我们先是通过单缝衍射实验中狭缝宽度与衍射范围之间的反比关系,体验到了著名的海森堡不确定关系式:
ΔxΔpx≥ℏ2(式11.1)
然后,我们用标准差解释了不确定度Δx,Δpx的含义,将不确定关系式变成了一个可以计算的概率问题。
但我们同时看到,不确定性关系的背后,包含的是坐标和动量之间的“联动关系”的信息,也就是坐标表象和动量表象之间的表象变换。要证明这个关系式,就要先找出两者之间的表象变换。
为了对表象变换有一个直观印象,我们通过回顾级联斯特恩−盖拉赫实验,给出了Sz和Sy两个方向的自旋表象下的变换矩阵。
而坐标和动量之间的变换,就相当于是将有限维的情形推广到无限维的情形,只是这种变换不再是以矩阵的方式呈现。
那么它会是什么样的变换呢?
下节课,我们就来瞧一瞧。
编辑于 2021-11-30 13:26
