物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》的第7课。
了解本系列其他文章,请收藏目录:
0) 开篇语
在第6课中,我们看到了量子力学原理的核心,简单说来,就是用矩阵的特征值和特征向量理论,来理解量子力学中物理量算符的本征值与本征态。
其中,本征值对应着可以被测量到的经典力学量的值,而本征态可以构成量子力学的研究对象态矢量的一组基底。
而在第6课的最后,我们用本征值和本征态的理解方式,粗略理解了原子能级的线性代数含义,并且将本征值关系和我们将要在以后重点讨论的定态薛定谔方程联系了起来。
我们看到,如果将定态薛定谔方程写成狄拉克符号表示的抽象形式:
$\small \hat{H}\left|a\right>=E_a\left|a\right> \quad\scriptsize{(式6.10)}$
那么它就是能量的本征值关系,和矩阵的特征值关系 $\small A\boldsymbol\alpha_k=\lambda_k\boldsymbol\alpha_k $在形式上完全一样。
这正是我们理解作为量子力学核心的薛定谔方程的重要线索。
不过,正如我们在第6课中提到过的一样,在薛定谔方程中,态矢量 $\small \left|\psi\right> $是以波函数 $\small \psi(x,t)$ 的形式存在的。
而我们知道,本征态是特殊的态矢量,而波函数是一个函数。那么紧接着问题就来了:
一个函数怎么就变成向量了呢?
本课就专门来回答这个问题。
1) 我们要讨论什么?
还记得吗?我们从第1课开始引入态矢量的时候,其实就一直围绕着基底与线性组合、内积与正交性……这些关于向量的代数运算和几何性质在讨论。
所以,讨论函数的向量性质时,我们也将从这几个概念着手去理解。
并且,以后我们会看到,它们不仅有助于我们理解波函数和薛定谔方程的物理和数学意义、还将有助于我们今后理解表象理论,理解傅里叶变换,并且进一步理解海森堡不确定性关系。
不过这都是后话了,现在,我们还是把思绪收回来,先随作者回顾一段作者自身的美妙经历。
不知道同学们还记不记得,高数课学到傅里叶级数的时候,书上提到过正交函数的概念:
如果定义在区间 $\small [a,b]$ 上的函数 $\small f(x),g(x)$ 满足:
$\small \int_a^b{f(x)g(x)\text dx}=0 \quad\scriptsize{(式7.1)}$
则称 $\small f(x),g(x)$ 在区间 $\small [a,b] $上相互正交。
第一次见到这个定义时,我困惑了很久,毕竟我们很难把抽象的函数想象成可以画在纸面上的向量(虽然函数也有图像,但这里的正交性显然不是两个函数的图像正交 )。
直到后来,我在某个暑假“顿悟”到了一种不严谨但比较形象的理解方式……
经过那次“顿悟”之后,我不仅理解了函数的向量性质,并且惊奇地发现傅里叶级数原来也自带了一点“几何意义”,这让我愉悦地度过了一个美妙的夏天。
接下来,就来和同学们分享这段感悟。
不过,在此之前,我们要先回到线性代数中,复习整理一下前面的课里一直在讨论的向量的几个性质,然后再看看如何将它们推广到函数上。
2) 基底、线性组合与内积
我们知道,给定一组正交基底 $\small {\boldsymbol e_1,\boldsymbol e_2,\cdots,\boldsymbol e_n}$ 后,一个 $\small n $维向量 $\small \boldsymbol a$ 可以表示为它们的线性组合:
$\small \boldsymbol a=\sum_{i=1}^{n}{a_i\boldsymbol e_i} \quad\scriptsize{(式7.2)}$
其中,线性组合的系数 $\small a_i$ 可以由 $\small \boldsymbol a $与 $\small \boldsymbol e_i $的内积计算:
$\small a_i=\frac{\left<\boldsymbol a,\boldsymbol e_i\right>}{\left|\boldsymbol e_i\right|^2} \quad\scriptsize{(式7.3)}$
这可以很容易地从代数上证明:
首先,根据线性组合关系:
$\small\begin{align} \left<\boldsymbol a,\boldsymbol e_i\right>&=\left<\sum_{j=1}^{n}{a_j\boldsymbol e_j},\boldsymbol e_i\right>\\&=\sum_{j=1}^{n}{a_j\left<\boldsymbol e_j,\boldsymbol e_i\right>}\\&=a_1\left<\boldsymbol e_1,\boldsymbol e_i\right>+a_2\left<\boldsymbol e_2,\boldsymbol e_i\right>+\cdots+a_n\left<\boldsymbol e_n,\boldsymbol e_i\right> \end{align} \quad\scriptsize{(式7.4)}$
由于 $\small {\boldsymbol e_1,\boldsymbol e_2,\cdots,\boldsymbol e_n} $是单位正交基,所以:
$\small \left<\boldsymbol e_j,\boldsymbol e_i\right>=\left<\boldsymbol e_i,\boldsymbol e_i\right>\delta_{ij}=\begin{cases} \left|\boldsymbol e_i\right|^2& i=j\\ 0& i\neq j \end{cases} \quad\scriptsize{(式7.5)}$
因此,上面的求和式中,除了 $\small a_i\left<\boldsymbol e_i,\boldsymbol e_i\right>$ 项以外,其余都为0。
最终得:
$\small a_i=\frac{\left<\boldsymbol a,\boldsymbol e_i\right>}{\left|\boldsymbol e_i\right|^2} \quad\scriptsize{(式7.3)}$
Q.E.D.
而上式的几何意义也很明确(至少在实数域上如此 ):
内积 $\small \left<\boldsymbol a,\boldsymbol e_i\right>=\left|a\right|\left|e_i\right|\cos{\theta_i}$ ,其中 $\small \theta$ 是 $\small \boldsymbol a $在 $\small \boldsymbol e_i$的夹角,因此内积 $\small \left<\boldsymbol a,\boldsymbol e_i\right>$ 的意义,就是向量 $\small \boldsymbol a$ 在基底$ \small \boldsymbol e_i$ 上的投影长度 $\small |a|\cos{\theta_i}$ 乘以$\small \boldsymbol e_i$ 的长度 $\small \left|\boldsymbol e_i\right|$
而如果将基底 $\small \boldsymbol e_i $的长度 $\small \left|\boldsymbol e_i\right| $作为单位长度,那么 $\small \boldsymbol a $的分量 $\small a_i $的几何意义,正好又是 $\small \boldsymbol a $在 $\small \boldsymbol e_i $上的投影长度与单位长度 $\small \left|\boldsymbol e_i\right| $之比,即 $\small a_i=\frac{|a|\cos{\theta_i}}{|\boldsymbol e_i|}$ (就像我们中学做矢量的正交分解一样 )
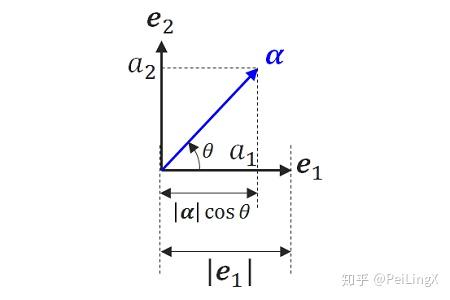
二维平面上的例子
因此 $\small \left<\boldsymbol a,\boldsymbol e_i\right> $和$ \small a_i $是正比关系,两者相差一个系数 $\small \left|\boldsymbol e_i\right|^2$
接下来,我们就要将基底、线性组合、内积、正交这些概念推广到函数上。
3) 函数的向量性质
我们先看看,如何将一个函数从形式上变成向量。
让我们来考虑一个定义在区间 $\small [a,b]$ 上的函数 $\small f(x)$
将 $\small [a,b]$ 分成 $\small n$ 个等间隔的小区间,每个区间的长度记为$ \small \Delta x$ ,则:
$\small \Delta x=\frac{b-a}{n} \quad\scriptsize{(式7.6)}$
然后,让函数在相邻区间的节点上取值,就可以得到一个离散数组:
$\small \left(f_0,f_1,f_2,\cdots,f_n\right) :=\left(f(a),f(a+\Delta x),f(a+2\Delta x),\cdots,f(b)\right) \quad\scriptsize{(式7.7)}$
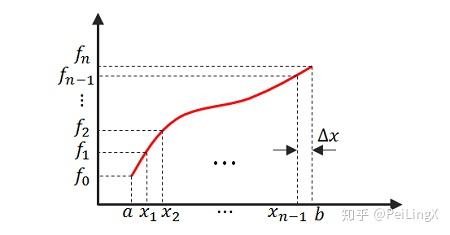
这是不是在形式上和向量 $\small (a_1,a_2,\cdots,a_n) $很像了?
但是这显然不够,因为向量是有内积运算、正交关系、线性组合关系等一系列性质的。
接下来,我们就先来抓住其中最关键的一条:内积。
我们先把两个向量的内积再写一遍:
$\small \left<\boldsymbol a,\boldsymbol b\right>=\sum_{i=1}^{n}{a_ib_i} \quad\scriptsize{(式7.8)}$
上面是对于定义在实数域上的向量而言的,而由于量子力学是复数的天下,我们会频繁看到复数域上取值的态矢量,所以我们要将这个定义推广到复数域上:
$\small \left<\boldsymbol a,\boldsymbol b\right>=\sum_{i=1}^{n}{a^*_ib_i} \quad\scriptsize{(式7.9)}$
(其中 $\small a^*_i $表示分量 $\small a_i $ 的共轭复数,就像我们在第2课里看到过的那样 )
根据这个定义,我们可以形式上类比着写出两个经过离散化的函数 $\small f(x),g(x) $的内积:
$\small \left<f,g\right>:=\sum_{i=0}^{n}{f^*_ig_i} \quad\scriptsize{(式7.10)}$
由于函数是定义在连续的实数区间上的,我们可以把小区间的个数 $\small n$ 无限细分下去(这也暗示着函数作为向量时、所在的向量空间是“无穷维”的 ),这样就能对前面定义的内积取极限:
$\small \left<f,g\right>:=\lim_{n\rightarrow\infty}{\left(\sum_{i=0}^{n}{f^*(x_i)g(x_i)}\right)} \quad\scriptsize{(式7.11)}$
但问题来了:由于 $\small f(x),g(x)$ 会取遍 $\small [a,b] $区间上的所有点,所以这个极限是发散的。
怎么办?
答案其实不难:我们知道,小区间个数 $\small n$ 趋近无穷的同时,小区间长度 $\small \Delta x$ 会趋近于0,所以我们可以考虑在求和式的基础上乘以 $\small \Delta x$ ,变成:
$\small \left<f,g\right>=\lim_{\Delta x\rightarrow0}{\left(\Delta x\sum_{i=0}^{n}{f^*(x_i)g(x_i)}\right)} \quad\scriptsize{(式7.12)}$
等一下,这个极限式是不是在哪见过?
你没看错,我们的确见过它,它就是黎、曼、积、分!
话说到这个份上,我们就不用再遮遮掩掩、可以直接给出函数内积的定义了:
$\small \left<f,g\right>=\int_{a}^{b}{f^*(x)g(x)\text dx} \quad\scriptsize{(式7.13)}$
而有了内积之后,函数的“正交性”也就呼之欲出:
当 $\small \int_a^b{f^*(x)g(x)\text dx}=0$ 时,函数 $\small f(x),g(x)$ 正交
对于定义在实数域上的函数而言, $\small f^*(x)=f(x) $,于是我们就得到了开篇语中提到的那个正交函数的定义:
$\small \int_a^b{f(x)g(x)\text dx}=0 \quad\scriptsize{(式7.1)}$
现在,明确了“正交”的概念,我们再来看看函数中的“正交基底”。
这些基底其实就是我们在高数课本里看到过的函数项级数,我们在以后解薛定谔方程的时候经常会遇到。
而“正交的”函数项级数中,我们最熟悉的例子就是傅里叶级数。
4) 傅里叶级数的“几何意义”
我们知道,一个以 $\small 2T$ 为周期的、满足一定条件(高数课本上提到过的Dirichlet条件,这里不去深究 )的周期函数 $\small f(x)$ ,可以展开成三角函数的级数和,即傅里叶级数:
$\small f(x)=\frac{a_0}{2}+\sum_{k=1}^{\infty} {\left[ a_k\cos{\left(\frac{k\pi x}{T}\right)}+b_k\sin{\left(\frac{k\pi x}{T}\right)} \right]} \quad\scriptsize{(式7.14)}$
而高数课本还告诉我们,其中的三角函数序列$\scriptsize \left\{\cos{\left(\frac{k\pi x}{T}\right)},\sin{\left(\frac{k\pi x}{T}\right)}\right\} $在一个周期内满足两两正交的关系:
$\small \begin{cases} \int_{-T/2}^{T/2} {\cos{\left(\frac{m\pi x}{T}\right)}\cos{\left(\frac{n\pi x}{T}\right)}\text dx} =\begin{cases} T& m=n\\ 0& m\neq n \end{cases}\\ \int_{-T/2}^{T/2} {\sin{\left(\frac{m\pi x}{T}\right)}\sin{\left(\frac{n\pi x}{T}\right)}\text dx} =\begin{cases} T& m=n\\ 0& m\neq n \end{cases}\\ \int_{-T/2}^{T/2} {\cos{\left(\frac{m\pi x}{T}\right)}\sin{\left(\frac{n\pi x}{T}\right)}\text dx}=0 \end{cases} \quad\scriptsize{(式7.15)}$
现在,有了对函数内积的理解,我们就能明白,这个三角函数序列恰好构成了一组正交基底。
而函数 $\small f(x)$ 的傅里叶级数就可以看成这组基底的线性组合:
$\small \begin{align} f(x)&=a_0\cos{0}+b_0\sin{0}+a_1\cos{\left(\frac{\pi x}{T}\right)}+b_1\sin{\left(\frac{\pi x}{T}\right)}+\cdots\\&=a_0+a_1\cos{\left(\frac{\pi x}{T}\right)}+b_1\sin{\left(\frac{\pi x}{T}\right)}+\cdots \end{align} \quad\scriptsize{(式7.16)}$
(是不是发现这个式子和高数课本上的傅里叶级数不太一样?别担心,我们后面会把它变成我们熟悉的样子 )
而根据向量线性组合的系数公式 $\small a_i=\frac{\left<\boldsymbol a,\boldsymbol e_i\right>}{\left<\boldsymbol e_i,\boldsymbol e_i\right>}$ ,我们可以类比着写出:
$\small \begin{cases} a_k=\frac{\left<f(x),\cos{\left(\frac{k\pi x}{T}\right)}\right>}{\left<\cos{\left(\frac{k\pi x}{T}\right)},\cos{\left(\frac{k\pi x}{T}\right)}\right>}\\ b_k=\frac{\left<f(x),\sin{\left(\frac{k\pi x}{T}\right)}\right>}{\left<\sin{\left(\frac{k\pi x}{T}\right)},\sin{\left(\frac{k\pi x}{T}\right)}\right>} \end{cases} \quad\scriptsize{(式7.17)}$
再根据函数内积的定义,可以分别算得:
$\small \begin{cases} a_0=\frac{\int_{-T}^{T}{f(x)\cos{0}\text dx}}{\int_{-T}^{T}{\cos^2{0\text dx}}} =\frac{1}{2T}\int_{-T}^{T}{f(x)\text dx}\\ a_k=\frac{\int_{-T}^{T}{f(x)\cos{\left(\frac{k\pi x}{T}\right)\text dx}}}{\int_{-T}^{T}{\cos^2{\left(\frac{k\pi x}{T}\right)\text dx}}} =\frac{1}{T}\int_{-T}^{T}{f(x)\cos{\left(\frac{k\pi x}{T}\right)\text dx}}\\ b_k=\frac{\int_{-T}^{T}{f(x)\sin{\left(\frac{k\pi x}{T}\right)\text dx}}}{\int_{-T}^{T}{\sin^2{\left(\frac{k\pi x}{T}\right)\text dx}}} =\frac{1}{T}\int_{-T}^{T}{f(x)\sin{\left(\frac{k\pi x}{T}\right)\text dx}} \end{cases} \quad\scriptsize{(式7.18)}$
$\small (k=1,2,\cdots)$
而为了让 $\small a_0 $和 $\small a_k{\ }(k=1,2,\cdots) $具有相同的表达式,我们钦定:
$\small a_0=\frac{\int_{-T}^{T}{f(x)\text dx}}{T} \quad\scriptsize{(式7.19)}$
于是傅里叶级数就变成了我们熟悉的样子:
$\small f(x)=\frac{a_0}{2}+\sum_{k=1}^{\infty} {\left[ a_k\cos{(\frac{k\pi x}{T})}+b_k\sin{(\frac{k\pi x}{T})} \right]} \quad\scriptsize{(式7.20)}$
而此时系数 $\small a_k,b_k $的“几何意义”也变得很明确:
它们就是 $\small f(x) $在一系列正交的三角函数基底上的“投影”。
换句话说,$ \small f(x) $可以看成某个“无穷维”向量空间里的一个向量,而傅里叶级数中的三角函数序列,就是这个“无穷维”向量空间中的一组基底组合成 $\small f(x)$ 的过程。
5) 总结与预告
通过一种不太严谨但比较容易理解的方式,我们理解了函数内积,从而理解了函数的向量性质,并且通过傅里叶级数的例子感受了它们的“几何意义”:
将满足一定条件的周期函数 $\small f(x)$ 看成某个“无穷维”向量空间里的向量,傅里叶级数中的三角函数序列,就是这个“无穷维”向量空间中的一组基底,傅里叶级数也就是将 $\small f(x) $展开成这组基底的线性组合。
而在后面的课程里我们将会看到,量子力学中的波函数,也是某个“无穷维”向量空间中的向量,这也就是为什么我们将它称作“态矢量”了。
到时候我们还将看到:薛定谔方程的解,通常也能表示成某种级数形式,而级数中的各项,也正好构成了一组基底,并且,这组基底,又刚好对应着某个算符的一组本征态……
再联想到我们在第6课中看到的、定态薛定谔方程 $\small \hat{H}\left|\psi\right>=E\left|\psi\right> $与矩阵特征向量关系 $\small A\boldsymbol\alpha=\lambda\boldsymbol\alpha $在形式上的相似,我们似乎马上要见证一个Eureka Moment的到来了。
到那个时候,我们将会见证到,态矢量、波函数、算符、本征值、本征态……这一堆的名词,终将在线性代数的引领下,完美地汇集到薛定谔方程中,完成“生命的大和谐”。
我们将从下节课开始揭晓。
编辑于 2021-11-30 13:23
