物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》的第4课。
了解本系列其他文章,请收藏目录:
0) 前情提要
在本系列的前两课里,我们通过有名的“薛定谔的猫”思想实验,介绍了量子力学的正确打开方式:态矢量,以及它的向量性质。
而在第3课里,我们又通过无名的(作者自编的 )“量子糖的故事”思想实验,体验了一次如何利用态矢量的向量性质来理解不确定性原理的思路。
但正如第三课结尾所说,量子糖只是一个用来贴近生活的虚构案例,而现在,我们就要进入真实的物理世界,来见识量子糖的现实版本:
斯特恩-盖拉赫(Stern-Gerlach)实验 (以下简称SG实验 )

两位大神镇楼
1) 背景介绍:电子的自旋
简单来说,SG实验主要验证的是电子的自旋展示出的量子特性。
所以,为了理解SG实验,我们需要先大概了解一下,什么是自旋(Spin)。
对于生活在宏观世界中的我们而言,“自旋”似乎是一个只存在于微观世界、听起来非常缺乏真实感的概念。但实际上,我们是可以通过某些宏观现象来感受到它的存在的。
比如这个看起来很理所当然、却又不太好回答的问题:磁铁为什么能吸引铁?

答案其实很简单,一句话就说完了:磁铁对铁的吸引力来自铁原子核外电子的自旋。
但我相信,听完这句话以后,很多同学应该是更懵圈了。
原创图片,转载请注明
没关系,我们一步一步来解释。
首先,我们来看一道中学物理题:在一个均匀磁场中放一个圆形闭合小线圈,线圈所在平面与磁场垂直,线圈上有逆时针方向的电流流过,那么这个线圈受到的总的安培力大小为多少?
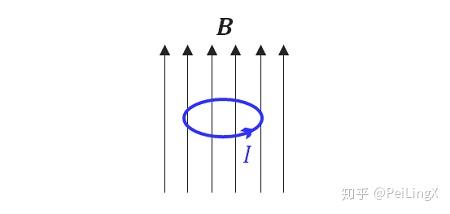
这个分析很简单:
在线圈上任取一段微元 $\small \text dl$ ,则它受到的安培力大小为:
$\small \text dF=BI\text dl \quad\scriptsize{(式4.1)}$
方向水平向外,将 $\small \text dF$ 在圆周上积分后,这些微元受力将会相互抵消,于是合力归为0.
现在,我们换个场景:有一个方向仍然是竖直方向、但磁感应强度大小沿着竖直方向变化的非均匀磁场,仍然将一个圆形闭合通电线圈垂直放到其中,那么它受到的合力是否还为0?
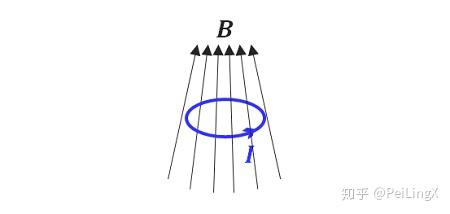
这个分析过程稍显复杂,我们这里不具体写出,只给出一个结论:
这种情形下,线圈将受到一个竖直向上的合力 $\small F_z$ ,其大小和电流强度 $\small I $、线圈围成的面积 $\small S$ 、磁感应强度的变化率 $\small \frac{\partial B}{\partial z}$ 成正比。
具体写出来就是:
$\small F_z=IS\frac{\partial B}{\partial z} \quad\scriptsize{(式4.2)}$
这里我们令 $\small \mu=IS$ ,并将其定义为一个新的物理量,叫作“磁矩”。
于是上面那个例子中,磁力、磁矩和磁感应强度的分布之间就有这样一个关系:
$\small F_z=\mu\frac{\partial B}{\partial z} \quad\scriptsize{(式4.3)}$
这里顺便说一句,磁矩其实是一个有方向的矢量,它的方向垂直于线圈所在平面,并且规定当电流方向为逆时针时磁矩为正(就像我们定义角速度方向一样 )。
所以上面那个式子其实有一个更普适的矢量式:
$\small \boldsymbol F=\boldsymbol\nabla (\boldsymbol\mu\cdot\boldsymbol B) \quad\scriptsize{(式4.4)}$
这里 $\small \boldsymbol\mu$ 和 $\small \boldsymbol B$ 的点乘说明了力的大小还和磁矩与磁场的角度关系有关,这个我们稍后再说。
现在我们只需要先定性地知道:一个闭合通电线圈放入不均匀磁场中,会受到一个力,其大小与磁矩大小、磁感应强度变化率以及磁矩与磁力线的夹角有关。
然后我们就来通过“磁矩”这个物理概念,理解“磁石召铁”的原理以及电子的自旋。
我们知道,物质的原子中,有电子绕原子核运动,这种运动(在经典物理图景中 )可以看成行星一样的圆周运动,于是会产生微观的环形电流,从而形成磁矩;
另一方面,电子自身还会有一种类似“自转”的性质(注意,不是真的自转! ),也会形成像环形电流一样的效果,从而形成磁矩。
一块铁被磁铁吸引,就是因为内部铁原子原本杂乱分布的磁矩、在磁场中出现了某种宏观上的倾向性,从而在磁铁的不均匀磁场中受到了力。
(至于为什么会出现这种倾向性,这是个大坑,要用统计力学来填,本系列无法驾驭…… )
而这种具有倾向性的磁矩,就来自于电子的“自转”(不是真的自转! )的贡献,它的正式名称,即是自旋(Spin),它产生的这种磁矩具有固定的大小,我们在后文就直接记为 $\small \mu $。
到此为止,我们就至少从宏观上大致感受到自旋是个什么概念了。
虽然各位一定还想弄清楚,这个莫名其妙的自旋为什么会存在,但要从根本上解释自旋的来源,我们还有很长的路要走。
所以现在我们暂时不去理会“自旋为什么会存在”这种难缠的问题,而是回到本文的主题:Stern-Gerlach实验。
2) SG实验概述
我们知道,由于物理空间存在各向同性的性质,因此对于含有大量原子的普通物质而言,其内部各个电子的自旋方向(也就是自旋产生的磁矩方向 )应该是随机的,并且在空间中各个方向上具有等概率的分布。
但这里有个问题:作为微观粒子,电子自旋方向的这种随机性,是我们在经典物理中理解的那种随机性?还是暗藏着某种量子特性?
揭示这个答案的,就是SG实验(虽然SG实验的本来目的并不是这个…… )。
我们先从这个实验最简单的版本开始说起。
最简单版本的实验装置包括:一个加热炉、两个挖了小圆孔的挡板、一对磁极和一个接收屏。
这里上个图,看看这套装置的样子:
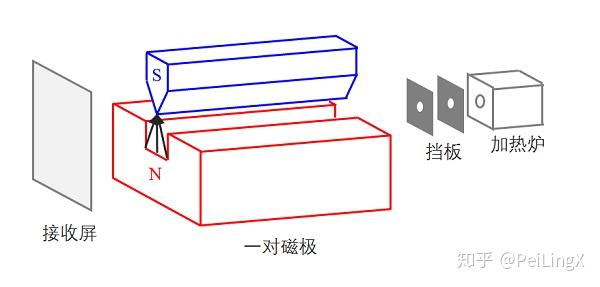
然后我们来看看SG实验的大概流程:
首先,我们将一堆白花花的银子放到加热炉里烧化,这样就会有很多银原子被蒸发出来,然后从炉子的开口中逸出。
顺便说一句,各位千万不要因为这些银子被“白白烧掉”而感到惋惜。其实,相比于被做成货币,它们能被用在这么伟大的实验上面,其实是一种更“崇高”的归宿。
(这两种归宿就像是殉教的圣女和夜总会坐台的小姐一样天差地别…… )
好了,回到正题,我们继续追踪银原子的去向。
从加热炉逸出的银原子中,大部分会被一前一后两个带小孔的挡板挡住,只有一小撮会从两个小孔中通过。于是这两个小孔就起到了定向筛选作用,筛出了沿着正 x 方向运动的银原子。
这些银原子通过两块磁铁间分布于 z 方向的不均匀磁场后,会到达接收屏,如下图。
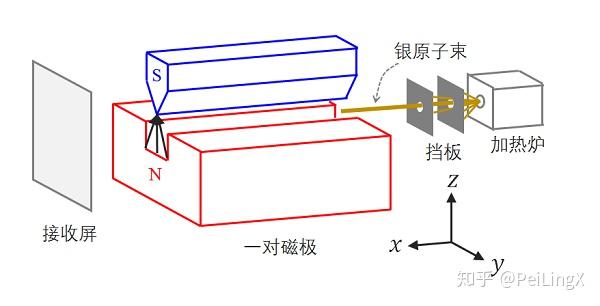
那么接下来问题来了:这些由大量银原子组成的银原子束,通过磁场后,会在接收屏上打出什么样的图案?
我们先从经典物理的假设出发来推测一下。
3) 基于经典物理的推测
首先,我们要知道一个事实:银原子虽然有47个核外电子,但其中46个电子的自旋磁矩都会相互抵消,最终只有最外层1个电子的自旋对整个银原子的磁矩做出贡献。
换句话说,银原子的整体磁矩大小就等于1个电子的自旋磁矩大小 $\small \mu $。
磁矩大小说完了,现在我们要来重点说说磁矩方向的影响,它是我们推测实验结果的关键。
而这就要用到前面提到的磁矩在磁场中受力的矢量式了:
$\small \boldsymbol F=\boldsymbol\nabla (\boldsymbol\mu\cdot\boldsymbol B) \quad\scriptsize{(式4.4)}$
首先,我们将 $\small \boldsymbol F=\boldsymbol\nabla (\boldsymbol\mu\cdot\boldsymbol B) $其展开成分量形式,就是:
$\small \begin{align} \boldsymbol F&=(F_x,F_y,F_z)\\ &=\left(\frac{\partial }{\partial x} (\boldsymbol\mu\cdot\boldsymbol B),\frac{\partial }{\partial y} (\boldsymbol\mu\cdot\boldsymbol B),\frac{\partial }{\partial z} (\boldsymbol\mu\cdot\boldsymbol B)\right)\\ &=\left( \boldsymbol\mu\cdot\frac{\partial \boldsymbol B}{\partial x}, \boldsymbol\mu\cdot\frac{\partial \boldsymbol B}{\partial y}, \boldsymbol\mu\cdot\frac{\partial \boldsymbol B}{\partial z} \right) \end{align} \quad\scriptsize{(式4.5)}$
考虑到在SG实验的装置中,磁感应强度只沿着 $\small z $方向变化,所以我们可以只关注$ \small F_z$ 分量:
$\small \begin{align} F_z&=\frac{\partial}{\partial z}(\boldsymbol\mu \cdot\boldsymbol B)\\ &=\boldsymbol\mu \cdot\frac{\partial\boldsymbol B}{\partial z}\\ &= \mu_x\frac{\partial B_x}{\partial z}+ \mu_y\frac{\partial B_y}{\partial z}+ \mu_z\frac{\partial B_z}{\partial z} \end{align} \quad\scriptsize{(式4.6)}$
同时,由于银原子从磁场的正中间进入,此处磁场竖直向下,只有 $\small z$ 分量有变化,于是:
$\small \frac{\partial B_x}{\partial z}=\frac{\partial B_y}{\partial z}\equiv0 \quad\scriptsize{(式4.7)}$
这样 $\small F_z$ 就简化为:
$\small F_z=\mu_z\frac{\partial B_z}{\partial z} \quad\scriptsize{(式4.8)}$
接下来,我们就用它讨论磁矩方向的影响。
按照经典物理的观念,进入磁场前,每颗银原子都已经有了一个确定的磁矩,磁矩的大小都是 $\small \mu$ ,但方向各不相同。
我们假设,某颗银原子进入磁场前,磁矩方向与$ \small +z$ 方向成 $\small \theta$ 角度,那么磁矩的 $\small z$ 分量就是:
$\small \mu_z=\mu\cos{\theta} \quad\scriptsize{(式4.9)}$
于是银原子飞入磁场后,受力大小就是:
$\small F_z=\mu\frac{\partial B_z}{\partial z}\cos{\theta} \quad\scriptsize{(式4.10)}$
有了这个式子,我们就可以讨论银原子打在屏幕上的图案了。
按照经典物理的理解,由于银原子的磁矩方向随机,所以不同的银原子的磁矩方向 $\small \theta$ ,可以在 $\small 0$ 到 $\small \pi $之间任意取值,并且机会均等;
相应地,不同的银原子受到的力 $\small F_z$ 的大小也就可以在 $\small -\mu\frac{\partial B}{\partial z}$ 和$ \small \mu\frac{\partial B}{\partial z} $之间任意取值;
于是,不同银原子在 $\small z$ 方向的加速度也可以从$ \small -\frac{\mu}{m}\frac{\partial B}{\partial z}$ 到 $\small \frac{\mu}{m}\frac{\partial B}{\partial z} $之间任意取值。
这样,通过磁场后的银原子的轨迹,也将可以在磁矩为 $\small \boldsymbol\mu $的银原子形成的轨迹和磁矩为 $\small -\boldsymbol\mu$ 的银原子形成的轨迹之间的平面上任意取值:
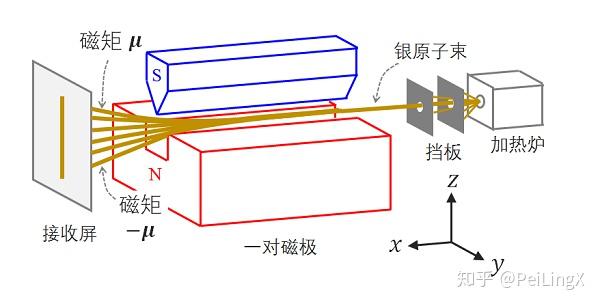
最后,当足够多个银原子打到接收屏上后,这些轨迹会在屏幕上形成一条 $\small z$ 方向上的连续线段(如上图 )。
这就是经典物理假设对银原子打在屏幕上的图案的猜测。
然而实际结果如何呢?
4) 实际结果
SG实验的实际结果是:银原子一进入磁场,就自动劈裂了泾渭分明的两条轨迹,最后在屏幕上打出两个分离的斑点,如下图:
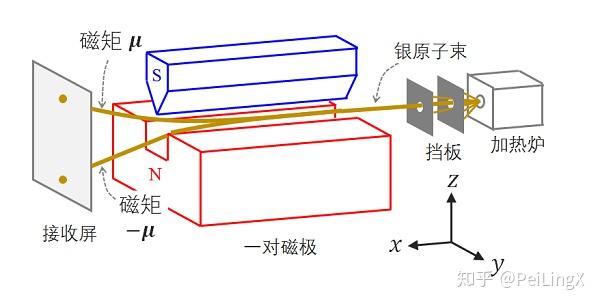
这就意味着,通过磁场的银原子的自旋磁矩方向,只有 $\small +z$ 和 $\small -z $两种,而没有中间值!
这看起来似乎就矛盾了:
明明银原子的磁矩是完全随机的,为啥在这个实验中反而变成两个“确定”的值了?
这就要从我们如何理解这种“随机”说起了。
5) SG实验结果的解释:如何理解随机性?
从经典观点来看,不同银原子的磁矩方向随机分布,但每个银原子的磁矩在进入磁场前就已经确定了,只是因为我们进行了类似“随机取样”的动作,所以整体看起来呈现随机性。
而假如我们一颗一颗去考察单颗的银原子,那么在经典世界里,我们会看到每颗银原子有一个确定的磁矩方向,这些具有各不相同的、确定磁矩方向的银原子,进入磁场后,最终就会走出一片连续分布的轨迹。
但实验结果却告诉我们,这个猜测并不对,实验结果背后隐藏的真正的随机性,其实是来自量子层面的。
那么,该怎么理解“量子层面”的随机呢?
这还是要从我们已经在前两课中学到的叠加态的角度来理解。
按照这种理解,对于任意一颗银原子,只要我们不去测量它在某个方向上(比如 z 方向上 )的磁矩,它就处于量子叠加态,而没有确定的方向。
而只有当我们去测量它的磁矩时,它才会随机坍缩到这个测量行为对应的本征态上,被我们测量到,换句话说,测量结果只能是被测量的物理量对应的本征态之一。
比如,如果我们去测量它在 $\small z$ 方向的磁矩,那么测量结果就只能是“ $\small z$ 方向磁矩”这个物理量的两个本征态,这正好就是“磁矩处于 $\small +z$ 方向”和“磁矩处于 $\small -z$ 方向”两个结果,于是我们就看到,大量银原子通过磁场后,会形成两条泾渭分明的轨迹。
类比到第3课中虚构的“量子糖”上面,就好像我们第一次品尝量子糖的味道前,味道处于叠加态一样,只有品尝行为发生后,我们才能得到“甜”或“酸”两种结果。
而同样道理,如果我们要去测量银原子在 $\small y$ 方向上的磁矩,那么我们也只能随机得到“磁矩处于 $\small +y $方向”或“磁矩处于 $\small -y $方向”两种结果,而不可能出现“磁矩处于与 $\small +y$ 方向成45°角”的情况。
再次类比到“量子糖”上面,就好像我们第一次观察量子糖的颜色前,颜色处于叠加态,只有观察行为发生后,才能得到“红”或“蓝”两种结果。
而在“量子糖”的例子中,我们还知道,当“品尝味道”和“观察颜色”两种行为交替进行的时候,会有一些奇怪的事情发生。
那么在真实的SG实验中,如果我们交替测量银原子 $\small z$ 方向的磁矩和 $\small y$ 方向的磁矩时,会不会也有一些奇怪的事情发生呢?
这个问题我们留到下一课再继续介绍,而现在,我们要来思考另一件有意思的事情。
6) 态空间与物理空间
首先来回顾我们在第2课中知道的一个“事实”:
一般情况下,一个物理量的不同本征态是(在抽象意义上 )相互正交的。
所以,在SG实验中,“ $\small z$ 方向磁矩”的两个本征态:“磁矩处于 $\small +z $方向”和“磁矩处于 $\small -z$ 方向”两个结果也是正交的。换句话说,它们在态空间中的“夹角”是 $\small \frac{\pi}{2}$ 。
那么问题就来了:我们知道,两个本征态对应着磁矩处于$ \small +z$ 方向和磁矩处于 $\small -z $方向,这两个方向在“真实的”物理空间中的夹角是$ \small \pi$ !
如果将两个本征态在态空间中的“夹角”记为 $\small \varphi$ 、在真实空间中的夹角记为 $\small \theta $,那么从上面的分析可以看出,它们之间似乎有着简单的倍数关系: $\small \theta=2\varphi$
而在后面我们还会看到,这个关系对于任意两个态矢量的“夹角”都成立。
也许有人要问了:这种关系仅仅是巧合、还是蕴含着更为精妙的数学结构?
关于这个,我们要到比较遥远的将来再来揭晓答案。
现在说这个,只是为了感受一下抽象的态空间和“真实”物理空间的区别、并且提醒我们在以后保持这个意识。
7) 下期预告
关于SG实验的来龙去脉以及背后蕴含的量子机理的介绍,到此就暂告一段落了。
不过,现在我们的SG实验还只完成了一半,就像我们在“量子糖”的故事中只品尝了“量子糖的味道”一样。
在下一课中,我们还要去发现,当我们在SG实验装置中做出类似于“交替品尝量子糖的味道和观察量子糖的颜色”这种行为时,会发生哪些有趣的事情。
同学们不妨先猜一猜这个实验的做法和结果。等我们到了第5课,再来看看你猜的对不对。
编辑于 2021-11-30 13:22
