物理学等 2 个话题下的优秀答主
本文是深度科普系列《从线性代数到量子力学》的第1课。
了解本系列其他文章,请收藏目录:
0) 一些常识与困惑
作为一群有点基础物理知识、也读过一些大众科普、却还没有真正踏进量子力学大门的局外人,对于量子力学,我们可能定性地知道一些常识性的概念和结论、但更多的是伴随着它们而来的各种困惑,这里随便写几个吧:
- 比如,我们知道,原子核外的电子具有看起来不合常理的分立能级,也就是只能取一些不连续的特殊值。那么这些特殊值是怎么来的呢?
- 电子在不同能级之间会“跳来跳去”进行跃迁,同时吸收或发射光子,这个跃迁是怎么发生的呢?
- 又比如,我们知道微观粒子具有波粒二象性,物理课本告诉我们,微观粒子既是粒子又是波,但我们其实只是记住了这句话,这种奇怪的二重性质有没有更好的理解方式呢?
- 而我们又知道,描述粒子波动性的是波函数,并且隐约知道所谓哥本哈根诠释:波函数可以用来计算粒子在某个位置出现的概率。那么这个奇怪的概率波要怎么和我们熟悉的经典物理量联系起来呢?
- 而决定波函数行为的是一个叫作薛定谔方程的微分方程,我们知道它在量子力学中的地位如同牛顿第二定律在经典力学中的地位,那么薛定谔方程的物理意义是什么?它和经典力学定律之间是不是也能联系起来呢?
- 另外,我们听说过海森堡不确定性原理,它告诉我们,有些物理量会像一对冤家一样不能同时具有确定值,比如位置和动量,一个确定了,另一个就变得随机。那么,造成两者不能同时确定的更深层次原因是什么呢?
- 最后,最让我们困惑的是,这一大堆现象和结论看起来完全是散装在一起的,表面上看不出任何联系,它们真的是来自同一个量子力学理论体系吗?
其实,这重重悬疑背后的本质,并不是想象中那么纷繁复杂、也并不高深莫测。只要我们理解了量子力学的基本思考方式、再用我们熟悉的线性代数搭建起量子力学的理论体系,一切都会真相大白。
在后面的旅程中,我们会一边理解量子力学的理论体系、一边看到这个理论体系开枝散叶、逐个解开我们前面提到的那些谜团。
只不过,理解量子力学理论体系需要时间慢工出细活,而眼下我们立即能做的,就是先感受一下量子力学的基本思考方式。
1) 量子力学的打开方式
看过那么多量子力学科普,我们脑中已经形成这样一种概念:
量子力学和经典力学是两套截然不同的理论体系。
那么现在问题就来了:
如果要用一句话说出经典力学和量子力学的本质区别,该怎么描述?
笼统地说,两者的本质区别,在于描述物理对象的方式不同。
说得再具体一点就是:
- 经典力学描述物理对象的状态,是用具体的力学量,比如位置、速度、动量、能量等……
- 而量子力学描述物理对象的状态的方式,说起来非常简洁,简洁到只需要一个词:叫做态矢量(State Vector)。
这里需要注意的是,这个态矢量不是经典物理中那种存在于我们熟悉的三维空间、有直观几何意义的矢量,它甚至不在我们所熟悉的任何概念中,而仅仅存在于一个我们人为定义的抽象空间里面。
但它的抽象给我们带来了一个好处,就是信息量足够大。实际上,从一个态矢量当中,我们可以提取出某个物理对象所有的经典力学量信息,这一点我们后面慢慢体会。
而我们本课开头那些困惑的答案、乃至整个量子力学的理论体系,也都可以从态矢量的角度出发去理解。
总之,理解了态矢量,我们就能找到量子力学的正确打开方式。
所以,在这个开篇第1课里,我们就从态矢量开始说起。
为了更形象地理解态矢量,我们不妨先从一个虚构的、但是更简单也更熟悉的例子着手,开始我们的观光之旅。
这个例子,就是地球人都知道、甚至广场舞大妈都能扯上两句的、自带网红光环的思想实验:薛定谔的猫。
2) 猫的叠加态
我们知道,在薛定谔猫的思想实验中,有一个盒子里装了三样东西:
一颗有一定几率发生衰变的粒子、一台可以被粒子的衰变触发的杀猫神器、和一只喜获量子力学史上最佳动物演员奖的猫。
当我们不打开盒子时,对于盒子外面的观察者而言,粒子的衰变状况就是一个不确定的波函数,相应地、猫就处于一种“既生又死”的叠加态。
我们也知道,要理解这种叠加态,就必须抛弃“非生即死”的经典观念、建立起一种“量子式”的思维方式。
这时候,本课的主角、“态矢量”就该出来救场了。
有的量子力学科普书会告诉我们:猫的这种“既生又死”的状态,是“生”和“死”两种状态的叠加,可以用一种名叫“狄拉克符号”的奇怪符咒来描述:
$\small \left|\psi\right>=\frac{1}{\sqrt{2}}\left(\left|{L}\right>+\left|{D}\right>\right) \quad\scriptsize{(式1.1)}$
画得再形象点就是这样
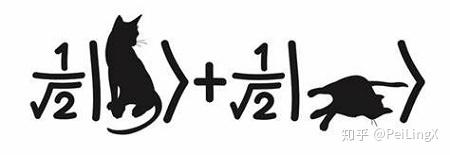
在这里, $\small \left|{L}\right> $表示生、$ \small \left|{D}\right>$ 表示死的状态,而描述“既生又死”的状态$ \small \left|\psi\right>$ ,是它们相加的形式。
(同学们一定很奇怪为什么前面会有个系数 $\small \frac{1}{\sqrt{2}}$ ,这里先留着这个疑问,我们后面会解释 )
而这些狄拉克符号( $\small \left|\psi\right>$,$\left|L\right>$,$\left|D\right>$ )所表示的,就都是描述猫的生死叠加态的态矢量。
不过需要说明的是,上面这个写法其实只是一种生死概率各占一半的特殊情况,对于更一般情况,叠加态应该写为:
$\small \left|\psi\right>= a_1\left|L\right>+a_2\left|D\right> \quad\scriptsize{(式1.2)}$
其中两个系数满足:
$\small |a_1|^2+|a_2|^2=1 \quad\scriptsize{(式1.3)}$
(后面我们会知道两个系数的含义 )
但不管是哪一种表示,我们都能看到,这个式子里出现了一个相加运算,这暗示着,这种“叠加”不是什么只可意会不可言传的玄学,而是可以从数学的角度来理解的。
这是一件值得庆贺的事情,因为作为一群理论物理的进阶票友,离奇变幻的物理现象和永恒不变的数学原理的契合,通常会给我们带来一种任何肉体和精神活动都无法代替的持久快感。
那么,怎么从数学上理解它呢?
同学们,抬头看看我们的标题是啥?是的,从线性代数到量子力学。
我们现在就要放出线性代数这位让人双腿发软的魔头了。

3) 复习课:向量的线性组合
我们先来看望一下线性代数中一位熟悉的老朋友:
向量的线性组合(Linear Combination)
我们知道,在一个线性空间中,如果给定一组线性无关的基底 $\small {\boldsymbol e_1 ,\cdots,\boldsymbol e_n}$,则向量空间中的任意向量 $\small \boldsymbol\alpha$ 都可以表示为基底的线性组合:
$\small \boldsymbol\alpha=a_1 \boldsymbol e_1+\cdots+a_n \boldsymbol e_n=\sum_{i=1}^{n}{a_i \boldsymbol e_i} \quad\scriptsize{(式1.4)}$
这个线性组合的几何意义,其实就是描述了向量和它在一系列基底上的投影之间的关系,就像中学物理经常见到的力的分解一样。
这意味着,我们可以将这种线性组合用几何的形式直观表示出来。
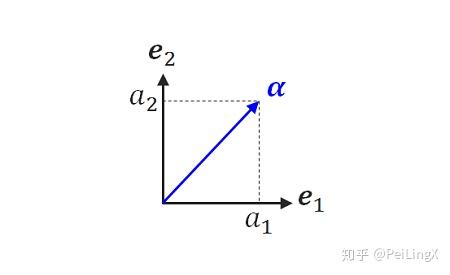
以二维平面为例:如果在平面上建立一个直角坐标系,那么两个坐标轴上就可以定义一组正交基底: $\small {\boldsymbol e_1,\boldsymbol e_2}$ 。
而平面上任意一个向量 $\small \boldsymbol \alpha$ 都可以表示为它们的线性组合:
$\small \boldsymbol \alpha=a_1 \boldsymbol e_1+a_2 \boldsymbol e_2 \quad\scriptsize{(式1.5)}$
4) “猫态”的数学描述
现在我们来将猫的叠加态和向量做个对比:
刚才我们提到,“既生又死”的状态可表示为 $\small \left|{L}\right>$ 和$ \small \left|{D}\right> $(即生和死 )两种状态的叠加:
$\small \left|\psi\right>= a_1\left|{L}\right>+a_2\left|{D}\right> \quad\scriptsize{(式1.2)}$
而二维平面上某个向量$\small \boldsymbol\alpha$可表示为两个基底 $\small{\boldsymbol e_1,\boldsymbol e_2}$的线性组合:
$\small \boldsymbol \alpha=a_1 \boldsymbol e_1+a_2 \boldsymbol e_2 \quad\scriptsize{(式1.6)}$
看着这样的数学形式,有没有什么想法?
是的,如果将 $\small \left|{L}\right> $和 $\small \left|{D}\right> $两种状态看成某个抽象的二维空间中的基底的话,那么那个“既生又死”的状态,就是这两个基底的线性组合。
现在,请同学们挺直腰板打起精神,理解这个叠加态最关键的部分来了:

我们知道,经典物理的观点认为,不管我们开不开盒子,猫的状态都处在一个确定的状态,要么生要么死,也就是我们用狄拉克符号表示的 $\small \left|{L}\right>$ 和 $\small \left|{D}\right>$ 。
用几何直观来表示,就意味着猫的状态只能是某个抽象二维空间(不是我们所说的二维平面 )中两个基底的其中一个,而不可能是这个抽象空间中的其他向量,也就是下图的样子:
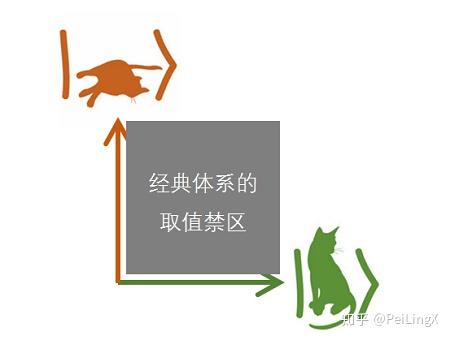
两个基底、也就是图中的绿色箭头和红色箭头,分别表示“活猫”和“死猫”两种状态。
经典体系下,猫的状态只能落在两个箭头中的一个,而无法出现在两者之间的灰色区域。
而在量子力学中,只要我们还没有去观测猫的死活,这只猫可以是两个基底 $\small \left|{L}\right> $和 $\small \left|{D}\right> $的任意线性叠加形成的抽象的向量,这也就是我们为什么将它称为“态矢量”的原因。
表示成几何直观,就是下图的样子:
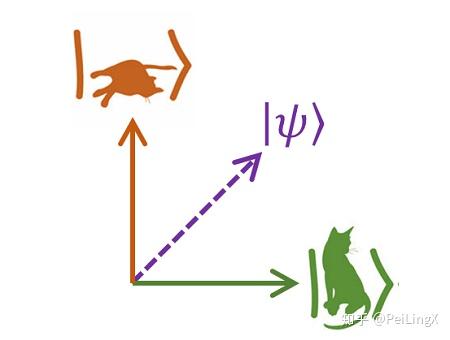
这也就意味着,在量子观点下,猫的状态可以在这个抽象二维空间上任意取值。
顺便说一句,这种任意性也让量子状态的取值比经典状态多了无穷多的自由度,这使得量子计算在某些算法上具有压倒性优势。不过这是题外话,我们有机会介绍量子计算时再聊。
至此,我们就粗略地认识了描述一个物理对象量子状态的态矢量、以及借用线性代数中的向量描述它的方式。
不过,我相信此时还有同学会觉得,用向量来描述这种不确定的叠加态似乎还是有些牵强,因为我们并没有看到更多的“向量性质”。
没关系,在下一课中,我们就会通过更多物理事实,来继续见证态矢量的向量意义。
而在本课的最后,我们要做一件十分重要的事情:将前面提到的这些概念梳理成规范的量子力学语言。毕竟我们是要正儿八经学一点量子力学的。
5) 几个重要术语
- 本征态
假设我们要关注某个物理量,记为 $\small F$ ,那么它可能被我们观测到的确定状态,在量子力学中叫做 $\small F$ 的本征态 (Eigenstate),也就是前面提到的基底。
(这句话也隐含了一个信息:不同物理量通常对应着不同本征态,这个我们以后会看到 )
而对于同一个物理量而言,除去某些特殊情况(将来我们会知道是什么特殊情况 ),它的不同本征态之间通常是正交的 (后面我们会体会到这个“正交”的物理意义 )
在薛定谔猫的例子中,我们观测的就是“猫的生死”这个假想的“物理量”,而我们能测到的结果,就是猫要么生要么死,不会有其他结果。
所以,“猫的生死”这个“物理量”的本征态就是两个正交的基底 $\small \left|{L}\right>$ 和 $\small \left|{D}\right> $(下节课我们会看到两个基底“正交”对应着什么样的物理意义 )
(当然,“猫的生死”并不是一个真正意义的物理量,但我们在这里姑且牺牲严谨性,将它作为一个比喻 )
另外,真实的物理量的本征态也通常不只是两个,而是有多个、甚至大多数时候是无穷多个。
这里我们不妨先来一点剧透:
对于原子核束缚下的电子而言,它的能量 $\small E $就有无穷多个分立的本征态$ \small {\left|E_n\right>}$
一个电子的状态可能是这一系列能量本征态的线性叠加,而一旦我们去观测它的能量,那么能观测到的结果只能是这些分立本征态当中的一个。
这也能对应上我们开篇提到的那些疑惑中的第一个:分立能级的来源。
当然,这还只是一种定性的理解,未来我们将会知道如何实实在在地计算分离能级、也就是能量的本征态。
这里顺便再说一句,本征态作为一组特殊的态矢量,又叫本征矢(Eigen Vector)。看到它的英文名,可能已经有同学想到了线性代数中的特征向量(*英文也是Eigen Vector* )。
而我们知道,特征向量通常是和一个矩阵联系起来的,因此Eigen Vector这个名字暗示着,一组本征态对应的那个物理量,也许可以用一个类似于矩阵的东西来描述。
如果同学们还记得,我们在一些科普书中听说过海森堡创立的“矩阵力学”,是不是已经感觉这背后还有更奇妙的风光等着我们?不着急,我们不久之后就会看到。
- 态空间
在薛定谔猫的例子中,我们看到,量子力学中,态矢量可以在本征态为基底张成的抽象空间中任意取值,而本征态张成的那个抽象空间,叫做态空间 (State Space)。
(再次提醒:态空间是一个抽象空间,而不是我们熟悉的欧氏空间,虽然我们出于几何直观的目的,可以将它与欧氏空间作一些类比 )
而任意态矢量都可以由一组本征态通过线性组合叠加而成(所以叫做叠加态 )。
(随时提醒:作为抽象的态空间中的向量,态矢量也是抽象的,和速度、动量这些经典物理中存在于三维空间中的矢量并不是一回事儿 )
- 狄拉克符号
在量子力学中,态矢量不再表示为线性代数中表示向量的加粗字母(比如 $\boldsymbol u$ ),而是用我们前面提到的狄拉克符号,即在一个竖线和一个箭头组成的符号 $\small \left|\right> $中插入一个字母,比如 $\small \left|\psi\right>$ 。
(另外,与这个竖线加右箭头的相对应的 $\small \left|\psi\right>$ 相对应的,还有左箭头加竖线的 $\small \left<\psi\right|$ ,它们分别成为右矢和左矢,详情我们下节课会提到 )
请记住这些概念和符号,以后它们将是我们量子力学课中的常客。
6) 总结与预告
本课中,我们找来那只网红猫,通过它的“既生又死”的叠加态,导出了量子力学中最根本的对象:态矢量。
然后,我们通过与二维平面上的向量的类比,将薛定谔猫奇怪状态的“物理意义”与线性代数中的向量性质联系了起来:
“生”和“死”两个经典世界中可以观测到的态,可以比喻成某个抽象二维线性空间中的基底,记为 $\small \left|{L}\right>$ 和 $\small \left|{D}\right> $,并称其为“猫的生死”这个“物理量”的本征态;
就像基底可以张成一个线性空间一样,本征态也能张成一个抽象空间,称作态空间;
那个存在于量子世界中的既生又死的叠加态,我们记作 $\small \left|\psi\right> $,可以看成作为基底的本征态的线性组合:
$\small \left|\psi\right>=a_1\left|L\right>+a_2\left|D\right> \quad\scriptsize{(式1.2)}$
而这一性质意味着,量子力学中的一个物理对象的状态可以在抽象的态空间中任意取值,而不像经典世界那样只允许存在生或死两个本征态。
不过,正如前面所说,用向量的线性组合描述猫的奇怪状态的想法,看起来仍然像是一次强行钦定的结果,显得并不是那么自然。
而且,我们在这里给出的线性组合中两个系数$ \small a_1,a_2 $的物理意义也还没有明确。
所以,在下一课里,我们就将解答这两个问题。
我们将看到,这个态矢量还蕴含着更多物理意义,而这些物理意义都可以用向量的特性来理解,并且显得非常自然、毫无违和感,而那两个系数的真实身份也即是其中一例。
编辑于 2021-12-14 16:16
