fmingde
版次: 2024
了解本系列其他文章，请浏览目录：
《大学物理》内容提要目录
§14 相对论
一、狭义相对论基本原理(爱因斯坦基本假设)
（1）爱因斯坦相对性原理: 在所有惯性系中，物理定律的表达形式都相同。
（爱因斯坦四个字不能省略,因为在经典力学中还存在伽利略相对性原理）
（2）光速不变原理: 真空中的光速是常量，它与光源或观测者的运动无关；在所有惯性系中，真空中的光速具有相同的量值$c=2.998\times 10^8 \rm m/s$ 。
二、狭义相对论的时空观
1. 洛伦兹坐标变换
参考系$S’(x’,y’,z’)$相对参考系$S(x,y,z)$沿$x$方向以速率$v$作匀速直线运动，则同一物理事件在两坐标系之间的时空坐标$(x’,y’,z’,t’)$、$(x,y,z,t)$之间满足以下变换关系：
$\begin{cases} x'=\gamma (x-vt)\\ y'=y\\z'=z \\t'=\gamma(t-\cfrac {vx} {c^2}) \end{cases}\quad \quad \begin{cases}x=\gamma (x'+vt')\\ y=y'\\z=z' \\t=\gamma(t'+\cfrac {vx'} {c^2}) \end{cases}$
$\gamma$：相对论系数，$\gamma=\cfrac 1 {\sqrt{1-\beta^2}}$ $\beta=\cfrac v c$
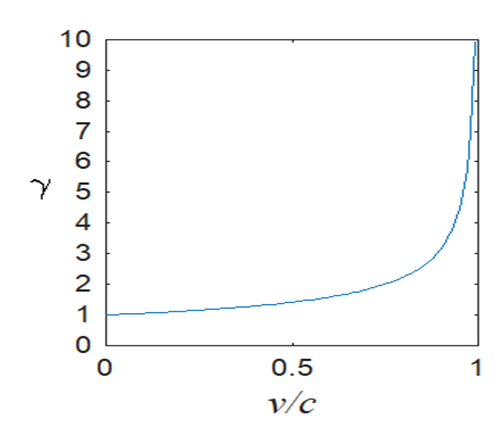
相对论系数通常为$1$，速度$v$接近光速时迅速增大，趋于无穷大。
推广：两个物理事件在$S’$系统中的时空间隔$(\Delta x’,\Delta t’)$ 和在$S$系中的时空间隔$(\Delta x’,\Delta t’)$ 满足的变换关系:
$\begin{cases} \Delta x'=\gamma (\Delta x-v\Delta t)\\ \Delta t'=\gamma(\Delta t-\cfrac {v\Delta x} {c^2}) \end{cases}\quad \quad \begin{cases}\Delta x=\gamma (\Delta x'+v\Delta t')\\ \Delta t=\gamma(\Delta t'+\cfrac {v\Delta x'} {c^2}) \end{cases}$
计算要求：★★时空间隔的变换
典型习题：二、9
2. 络伦兹速度变换
$u_x'=\cfrac {u_x-v}{1-\cfrac v {c^2}u_x} \quad \quad u_x=\cfrac {u_x'+v}{1+\cfrac v {c^2}u_x'}$
只需掌握沿运动方向（$x$方向）的速度变换。
3. 狭义相对论的时空观
（1）同时性的相对性
在一个惯性系中同时同地发生的两个事件，在另一个惯性系中观察是同时发生的。
在一个惯性系中同时不同地发生的两个事件，在另一个惯性系中观察就不是同时发生的。
（2）时间膨胀（时间延缓）
$\Delta t=\cfrac {\Delta t_0}{\sqrt{1-\beta^2}}=\gamma\Delta t_0$
$\Delta t_0$固有时: 相对事件发生地静止的观察者测出
$\Delta t$运动时: 相对事件发生地运动的观察者测出
运动时大于固有时，固有时最短。相对“事件发生地”的时间标准，其他惯性参考系中的时间“膨胀(增大)”了。
又称为动钟变慢效应、或时间延缓效应：相对观察者运动的钟比相对观察者静止的钟走得慢。
“相对观察者运动的钟”显示的是“动钟”所在参考系中的固有时，“相对观察者静止的钟”显示的是相对应的运动时。前者走得慢，时间值小，后者走得快，时间值大，固有时小于运动时，与前述“时间膨胀”的描述是一致的
在运用时间膨胀规律时，需要注意“固有时间”的定义：同一地点，前后两时刻之差。在涉及时间间隔的问题中，若前后两时刻不是同一地点标定的，不能将其作为固有时间进行换算，需用洛伦兹变换式解决
计算要求：★★★时间延缓公式的应用
典型习题：三、3
（3）长度收缩
$l=l_0\sqrt{1-\beta^2}=\cfrac {l_0} \gamma$
$l_0$固有长度: 相对被测长度静止的观察者测出
$l$运动长度: 相对被测长度运动的观察者测出
运动长度小于固有长度，固有长度最长。
在运用长度收缩规律时，需要注意“运动长度”的定义：指同一时刻，首尾两端坐标的差值。在涉及距离的问题中，若发现所讨论的距离不是同一时刻标定的，则不能套用以上关系，需用洛伦兹变换式解决。例如，跑步，从A到B点的距离，不能用长度收缩公式计算)
计算要求：★★★长度收缩公式的应用
典型习题：近代综合练习：三、1
三、狭义相对论动力学基础
1. 相对论质量
$m=\cfrac {m_0}{\sqrt{1- (\cfrac v c )^2}}=\gamma m_0$
质量是相对的，与参考系有关。当物体具有（相对观察者）的速度$v$时，在观察者参考系中，（运动）质量 $m$ 是物体自身参考系中（静止）质量 $m_0$ 的$\gamma $ 倍。
2. 相对论动量
$p=mv=\cfrac {m_0v} {\sqrt{1- (\cfrac v c )^2}}=\gamma m_0 v$
动量是（运动）质量与速率的乘积。在数值上，是静止质量与速率乘积的 $\gamma $ 倍。
3. 相对论能量
（1）质能关系
$E=mc^2$
建立的能量和质量的直接对应关系：具有质量的物体，其相对论能量是质量与光速平方的乘积。
（2）静能
$E_0=m_0c^2$
分子或原子间势能，分子或原子的动能等物质的内部能量。
（3）动能
$E_k=E-E_0=mc^2-m_0c^2$
相对论动能等于总能量与静止能量之差，动能的增加对应运动质量的增加。
当说一个物体在当前参考系中运动 (有速度时)，其能量是比从物体自身参考系看大一些，“大”出的这一部分，是其在观察参考系中表现出来的动能
经典力学中的动能 $E_k=\cfrac 1 2mv^2$是相对论动能的一阶主项。
4. 动量和能量的关系
$E^2=E_0^2+p^2c^2$
可按勾股定理”记忆: 总能量为直角三角形斜边，静能和$pc$为直角边。
计算要求：★能量、静能、运动速度等的计算
典型习题：三、6 近代综合练习: 三、２
§15 量子物理
一、光的粒子性(早期量子论)
1. 黑体辐射规律
（1）热辐射
物体中分子、原子受热激发而发射电磁波的现象
（２）黑体
能完全吸收照射到它上面的各种频率的电磁辐射的物体称为(绝对)黑体。黑体是一种理想化模型。
注意: 黑体仅是从吸收的角度来定义的。黑体同时存在热辐射，故黑体不一定是黑色的。实事上，好的吸收体同时是好的吸收体，黑体是同等条件下，辐射最强的物体。
（3）黑体模型
用不透明材料制成一空心容器，壁上开一小孔，小孔可看成黑体。
（4）斯特藩-玻尔兹曼定律
黑体辐出度与温度的四次方成正比。
$M(T)=\sigma T^4$
其中$\sigma$为斯特藩常量，$\sigma =5.67\times 10^{-8} \;\rm Wm^{-2}K^{-4}$
（5）维恩位移定律
黑体单色辐出度的峰值波长与温度成反比。
$\lambda_m T=b$
其中$\lambda _m$ 为单色辐出度的峰值波长，$b$为常数， $b=2.898\times 10^{-3}\;\rm mK$（6）普朗克黑体辐射公式
$M_\lambda(T)=\cfrac {2\pi hc^2}{\lambda^5}\cfrac {1}{e^{\frac {hc} {\lambda kT}}-1 } $
计算要求：★黑体辐射规律(两个定律)的应用 (常数$\sigma $ 、$b$ 不需要记，题目中会给出)。
典型习题：三、1
2. 普朗克能量子假设
为了解释黑体辐射规律，普朗克提出能量子假设。
黑体模型中电子的振动可视为一维谐振子，其吸收或发射的能量是不连续的，只能取一些特定的分立值。吸收或发射的最小基本能量单元称为能量子。
能量子的能量与振子的频率成正比，即
$\varepsilon=h\nu$
其中$h$为普朗克常数， $h=6.626\times 10^{-34}\;\rm Js$
3. 爱因斯坦光子假说
频率为 $\nu$的光束可看成是由大量能量等于$h\nu$ 的光子所构成的粒子流。
光具有波粒二象性，其能量、动量与频率、波长的关系为：
$\varepsilon=h\nu \quad \quad p=\cfrac h \lambda $ （其中频率和波长满足$\nu\lambda=c$）
光子能量和动量的联系为 $\varepsilon=pc$
计算要求：光子属性的计算,融合在其他计算内容中
4. 光电效应
（1）光电效应实验规律
金属中的电子能在光的作用下从金属表面上发射出来。
实验规律: 1）光电流与加速电压U有关，随着加速电压的增大，光电流趋于饱和(趋于饱和电流); 要使光电流降为０，需加反向的遏制电压$-U_0$ ，由$U_0$ 可测量逸出光电子的最大初动能；2）饱和光电流大小与光强成正比，与入射光频率无关；3）光电子的最大初动能与频率有关，入射光频率低于截止频率$\nu_0$ ，光电子无法逸出，高于$\nu_0$ 时，光电子最大初动能随频率增加而增大。
（2）爱因斯坦光电效应方程,光子理论对光电效应的解释
金属中的电子吸收一个光子的能量$h\nu$ ，一部分用于作功使金属中电子挣脱原子的束缚成为光电子，另一部分变为光电子的初动能。
$h\nu=\cfrac 1 2 mv_m^2+W$
式中$W$ 为光电子的(最小)逸出功， $\cfrac 1 2mv_m^2$为光电子的最大初动能。
计算要求：★光电效应计算(光子频率，光电子最大初动能，截止频率等)
典型习题：近代综合练习: 三、3
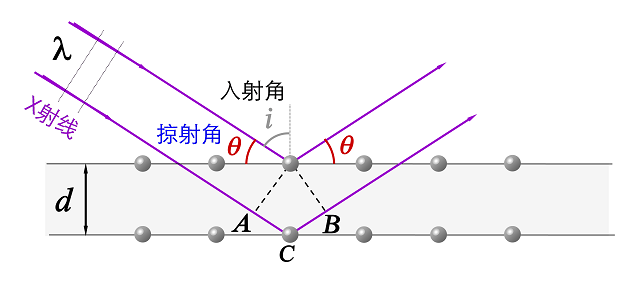
5. 康普顿效应
（1）康普顿效应
$X$射线散射实验中，散射线中除有波长和入射线$\lambda_0$相同的成分外，还有波长$\lambda \gt \lambda_0$ 的成分。
（2）光子理论对康普顿效应的解释
入射$X$射线光子与散射物质外层电子发生弹性碰撞，能量降低，波长变长。
入射$X$射线光子与散射物质内层电子发生弹性碰撞，能量不变，波长不变。
（3）康普顿偏移
波长偏移量（康普顿偏移）：$\Delta\lambda=\lambda-\lambda_0$
康普顿公式: $\Delta \lambda =\cfrac {2h} {m_0c}\sin^2\cfrac \theta 2$
其中$\theta$ 为散射角, $m_0$为电子的静止质量，$m_0=9.11\times 10^{-31}\;\rm kg$ ，$\cfrac h {m_0c}=2.43\times10^{-12}\;\rm m$ ，称为康普顿波长。
计算要求：★康普顿散射波长计算及光子、电子弹性碰撞的计算(动量守恒、能量守恒）
典型习题：三、2
二、量子力学基础
1. 德布罗意物质波假设
实物粒子具有波粒二象性
$\varepsilon =h\nu \quad \quad p=\cfrac h \lambda $
统计解释: 某处物质波的强度与粒子在该处邻近出现的概率成正比。
计算要求：★物质波波长、频率
典型习题：三、5
2. 海森伯不确定关系
对于微观粒子，不能同时用确定的位置和确定的动量来描述。坐标和动量的不确定性是相互联系的，满足:
$\Delta x \Delta p_x \ge h \quad \Delta y\Delta p_y \ge h \quad \Delta z \Delta p_z \ge h$
另，能量和时间的不确定性也存在关联，满足
$\Delta t \Delta E \ge h$
计算要求：★★不确定度的计算
典型习题：三、3(2),(3) ， 4
3. 波函数及其统计解释
量子力学中用波函数$\it \Psi(x,y,z) $ 描述微观粒子运动
$\vert {\it \Psi } \vert ^2 =\it \Psi \Psi^*$ 表示在某处单位体积内粒子出现的概率
波函数必须是单值、连续、有限的函数.
波函数必须满足归一化条件 $\int \vert {\it \Psi} \vert^2 {\rm d}V=1$
计算要求：★★★1) 用归一化条件，确定待定系数 2) 已知波函数，求解粒子运动属性(概率)
典型习题：三、6
4. 薛定谔方程
定态薛定谔方程
$\nabla^2 {\it \Psi}+\cfrac {8\pi ^2 m} {h^2}(E-E_p)=0$
5. 一维无限深势阱问题
粒子势能$E_p$ 满足: $0<x<a$处$E_p=0$，$x \le 0,x \ge a$处$E_p=\infty $ 。
波函数为驻波形式，阱壁处为波节，波腹的个数与量子数 $n$ 相等
$\psi(x)= \begin{cases} 0 &(x \le 0, x\ge a)\\ \sqrt{ \cfrac 2 a}\sin\cfrac {n\pi} a x & (0<x<a ) \end{cases} $
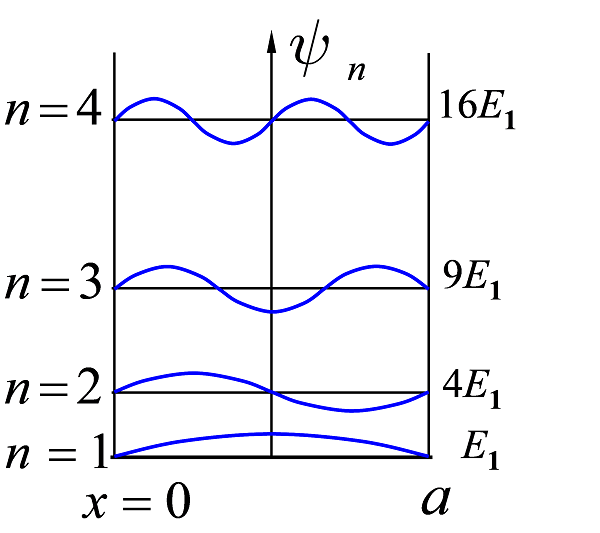
计算要求：波函数的讨论 (概率最大位置)计算，常以势阱问题为题材。
6. 对应原理
量子力学对应原理: 极限条件下，量子化规律可以转化为经典规律。
普遍的对应原理: 任何一个新的理论的极限情况必须与旧理论一致。
三、原子的壳层结构
1. 氢原子光谱
光谱规律 1）分立的线状；2）波数等于两个光谱项之差；3）可有规律地划分多个谱线系。
2. 玻尔的氢原子理论(早期量子论解释)
（1）三条假设
1）定态假设: 电子可在特定圆轨道上运动，处于定态，具有一定能量
2）量子化条件：电子绕核运动时，角动量只能是$\cfrac h {2\pi}$的整数倍
$L=n\cfrac h {2\pi}=n \hbar \quad n=1,2,3\ldots$
$n$称为 主量子数，$\hbar=\cfrac h {2\pi}$ :约化普朗克常量
3）跃迁规则: 电子轨道跃迁时，发出特定频率的光子
$h\nu =\vert E_i - E_f\vert$
（2）轨道半径
$r_n=n^2r_1$
其中 $r_1$为第一轨道半径(玻尔半径)
（3）轨道能量
$E_n=\cfrac {E_1} {n^2} \quad \quad n=1,2,3\ldots $
$E_1=-\cfrac {me^4}{8\varepsilon_0^2h^2}=-13.6\;\rm eV$ ，为基态$(n=1)$能量
计算要求：★★★氢原子吸收、发射光子问题(激发后产生哪些光谱谱线、最长、最短波长、画跃迁图)
典型习题：三、3(1) 近代综合练习: 三、4
3. 量子力学的氢原子理论
氢原子中的电子的运动状态可由四个量子数$(n,l,m_l,m_s)$ 来表示
（1）能量量子化和主量子数 $n$
主量子数$n$ 决定电子的能量 $E_n=\cfrac 1 {n^2}E_1$
$E_1$为基态能量
（2）角动量量子化和角量子数 $l$
角量子数$l$ 决定电子的轨道角动量（大小）
$L=\sqrt{l(l+1)}\cfrac h {2\pi} \quad \quad l=0,1,2,3,\ldots,(n-1)$
（3）空间量子化和磁量子数 $m_l$
磁量子数 决定轨道角动量的方向
$L_z=m_l \cfrac h {2\pi}\quad \quad m_l=0,\pm 1,\pm 2,\ldots,\pm l$
$L_z$为轨道角动量 $L$在外磁场方向的投影
（磁量子数由塞曼效应实验发现）
（4）自旋磁量子数 $m_s$
决定自旋角动量的方向
$S_z=m_s\cfrac h {2\pi}\quad \quad m_s=\pm \cfrac 1 2$
$S_z$为自旋角动量 $S$在外磁场方向的投影
（自旋量子数由施特恩-格拉赫实验发现）
4. 原子的壳层结构
1）原子中电子运动状态由四个量子数描述(与氢原子理论相同)
2）泡利不相容原理: 在一个原子中，不可能有两个或两个以上电子具有完全相同的量子数。
3）主量子数$n$ 相同的电子组成一个主壳层，每个主壳层能容纳 $2n^2$个电子。
4）主壳层中，按角量子数$l$分为若干支壳层，支壳层常采用“$s, p, d, f, g…$”标记，“$s$”对应$l=0$，“$p$”对应$l=1$，依次类推。每个支壳层能容纳$4l+2$个电子。
5）能量最小原理：原子系统处于正常状态时，每个电子总是趋于占有最低的能级。
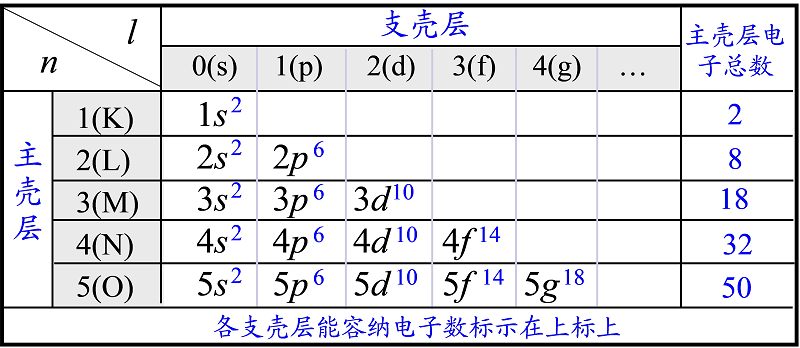
计算要求：★计算某壳层、某支壳层所能容纳的电子数目
典型习题：三、7
四、激光
1. 产生条件
1）工作物质具有粒子数反转的能级结构 2）具有谐振腔
2. 激光特性
1）方向性好 2）单色性好 3）能量集中 4）相干性好
五、半导体
1. 能带理论
晶体中，原子的能级分裂成为能带。相邻能带之间是禁带。
绝缘体、导体、半导体的区别在于能带结构中的禁带宽度。
2. 半导体
半导体的能带结构：(相对绝缘体而言)禁带宽度较窄
$n$型半导体，电子型半导体，掺杂5价元素，提供施主能级，提高电子载流子密度。
$p$型半导体，空穴型半导体，掺杂3价元素，提供受主能级，提高空穴载流子密度。
计算要求：可由禁带宽度，计算固体能吸收的辐射波长
典型习题：三、8,9
六、备注:本章计算中常用常数(需熟记)
1. 真空中的光速 $c=3\times10^8\;\rm m/s$
2. 普朗克常数 $h=6.63 \times 10^{-34}\;\rm Js$
3. 电子伏特 $1 \;\rm eV=1.6\times 10^{-19}\;J$
微观粒子的能量，需采用电子伏特单位
